Kezdőlap


Cím:	Az ,,áprilisi tréfás feladatok'' megoldása
Szerző(k):	Bíborka T. , Bollobás B. , Bondy T. , Borncs Klára , Czinege I. , Endrődy T. , Fenyő G. , Füle K. , Garamszegi P. , Hadik Z. , Hainzmann J. , Halász G. , Hank Zs. , Kolonits F. , Majtényi Sándor , Máthé Csaba , Nemezt T. , Pósch Margit , Pödör B. , Rohrböck Krisztina , S. Nagy Erzsébet , Soós T. , Szász D. , Szász Domonkos , Szatmári íg. , Toldy-Ősz Mária
Füzet:	1958/november, 121 - 123. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A szerkesztőségnek tömérdek munkája van. Arra kéri olvasóit, segítsenek a munkában, döntsék el, közölnék-e a lapban az alábbi két feladatot, illetőleg az alábbi két megoldással közölnék-e.
1. feladat: Bizonyítsuk be, hogy

\begin{matrix} \frac{1 + a + a^{2} + ... + a^{n - 1} + a^{n}}{a + a^{2} + ... + a^{n - 1}} ≧ \frac{n + 1}{n - 1}, \end{matrix}

a > 0

és

n

1

-nél nagyobb természetes szám.

Megoldás: A számtani közép nem kisebb a mértani középnél. Ezt a számlálóban, majd a nevezőben álló számokra felhasználva

\begin{matrix} 1 + a + a^{2} + ... + a^{n - 1} + a^{n} ≧ (n + 1) \sqrt[n + 1]{1 \cdot a \cdot a^{2} ... a^{n - 1} \cdot a^{n}}, \\ a + a^{2} + ... + a^{n - 1} ≧ (n - 1) \sqrt[n - 1]{a \cdot a^{2} ... a^{n - 1} .} \end{matrix}

Mindkét oldalon pozitív mennyiségek állnak, tehát a két egyenlőtlenség hányadosát véve kapjuk, hogy

\begin{matrix} \frac{1 + a + a^{2} + ... + a^{n - 1} + a^{n}}{a + a^{2} + ... + a^{n - 1}} ≧ \frac{n + 1}{n - 1} \cdot \frac{\sqrt[n + 1]{a^{1 + 2 + ... + n}}}{\sqrt[n - 1]{a^{1 + 2 + ... + n - 1}}} = \\ = \frac{n + 1}{n - 1} \cdot \frac{\sqrt[n + 1]{a^{\frac{(n + 1) n}{2}}}}{\sqrt[n - 1]{a^{\frac{(n - 1) n}{2}}}} = \frac{n + 1}{n - 1} \cdot \frac{a^{\frac{n}{2}}}{a^{\frac{n}{2}}} = \frac{n + 1}{n - 1} . \end{matrix}

Ezzel a bizonyítandó egyenlőtlenséget igazoltuk.

‐ A feladat állítása helyes, bizonyítottuk is lapunk XV. köt. 5. számában a 151‐152. o. a 822. feladatban. A megoldásban azonban hiba van: pozitív tagú és egyező értelmű egyenlőtlenségeket egymással osztva a kapott egyenlőtlenség már nem föltétlenül lesz helyes; pl.

\begin{matrix} 8 > 6, 2 > 1, \end{matrix}

de a két oldal hányadosát véve

4

már nem nagyobb, mint

6

.
Máthé Csaba (Győr, Révai g. II. o. t.)

‐ Megjegyezzük, hogy a 822. feladatra többen az itt közölt ,,megoldás''-t küldték be a feladat kitűzése idején.

2. feladat: Egy paralelogramma területe

100 {cm}^{2}

. A négyszöget átlói négy háromszögre bontják, amelyek közül kettő-kettő egybevágó. Az egyik háromszög területe

20 {cm}^{2}

. A másik (vele nem egybevágó) háromszögben szereplő paralelogramma-oldalon nyugvó két szög

30^{\circ}

, ill.

20^{\circ}

. Milyen hosszú az említett paralelogramma-oldal?

Megoldás: A paralelogrammát egy átlója két egybevágó háromszögre bontja, így egy ilyen háromszög területe

50 {cm}^{2}

. A másik átló meghúzásával ez két háromszögre bomlik; mivel egyik területe

20 {cm}^{2}

, a másiké

30

. Ha a kérdéses paralelogramma-oldalt

x

-szel jelöljük, az

x

oldalból és a három ismert szögből ‐

20^{\circ}

30^{\circ}

ill.

180^{\circ} - (20^{\circ} + 30^{\circ}) = 130^{\circ}

‐ a háromszög területe ismert tétel alapján meghatározható:

\begin{matrix} \frac{x^{2} sin 20^{\circ} sin 30^{\circ}}{2 sin 130^{\circ}} = 30, \end{matrix}

Ebből

\begin{matrix} x = \sqrt[]{\frac{60 sin 50^{\circ}}{sin 20^{\circ} sin 30^{\circ}}} . \end{matrix}

A kérdéses paralelogramma-oldalt kiszámítottuk. Ebből a szögfüggvényértékeket logaritmustáblából kikeresve s a műveleteket elvégezve

x

számértékét közelítőleg is megkaphatjuk.

‐ A két átló meghúzásával a paralelogrammát négy háromszögre osztjuk, amelyek közül kettő-kettő egybevágó. Tekintsünk ezek közül egy-egy nem egybevágót s vegyük alapjuknak a közös félátlót. Ehhez az oldalhoz tartozó magasságai is egyenlőek, s így a két nem egybevágó háromszög területe: az alap és magasság szorzatának fele, egyenlő lesz. A két átló a paralelogrammát tehát négy egyenlő területű háromszögre bontja.
Ha a teljes paralelogramma területe

100 {cm}^{2}

, a negyedrésze nem lehet

20 {cm}^{2}

, a példa tehát fölösleges és ellentmondó adatokat tartalmaz. Ha az adatok közül az összterületet

120 {cm}^{2}

-nek vesszük, a

20 {cm}^{2}

-t pedig elhagyjuk, akkor a megoldás lényegében helyes.
Majtényi Sándor (Miskolc, Kilián g. III. o. t.)

3. feladat: A világűr rakéta a Marsba érkezik. Az utasok egy iskolát látogatnak meg. Egy üres tanterem tábláján befejezetlen szorzáspéldát látnak: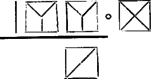

Megértik a vonaldarabok számából, hogy a befejezetlen művelet arab számokkal:

\begin{matrix} \frac{177 \cdot 6}{5} . \end{matrix}

A marslakók számrendszerének, úgy látszik, nem tíz az alapszáma. Gondolkozni kezdenek, hogy akkor mi lehet.
Gondolkozzunk mi is, és fejezzük be a szorzást!

Megoldás: A kijelölt szorzásban az eredmény utolsó jegye

5

, ez úgy lehetséges, hogy az utolsó jegyet megadó

6 \cdot 7 = 42

szorzatból maradékként

37

-et választunk le. A

37

az ismeretlen alapszámnak egész számú többszöröse. Az alapszámnak pozitívnak kell lennie. Mivel

37

törzsszám, az alapszám csak

1

vagy

37

lehet. A műveletben

1

-nél nagyobb számok is szerepelnek, ezért az alapszám csak

37

lehet.
A kijelölt szorzás tehát:

\begin{matrix} (1 \cdot 37^{2} + 7 \cdot 37 + 7) \cdot 6 = 6 \cdot 37^{2} + 42 \cdot 37 + 42 = \\ = 6 \cdot 37^{2} + (37 \cdot 37 + 5 \cdot 37) + (37 + 5) = 7 \cdot 37^{2} + 6 \cdot 37 + 5. \end{matrix}

A szorzás tehát a marslakók számrendszerében:

\begin{matrix} \underset{̲}{177} \cdot 6 \\ 765 \end{matrix}

Szász Domonkos (Bp. V., Eötvös g. III. o. t.)

A legszabatosabban indokolt megoldásokért könyvjutalmat nyertek:
Czinege Imre (Pannonhalma, Bencés g. III. o. t.),
Fenyő Gábor (Bp. V., Eötvös g. II. o. t.),
S. Nagy Erzsébet (Makó, József A. g. III. o. t.).

Sorshúzás alapján vigaszdíjként könyvjutalomban részesültek:
Bollobás Béla (Bp. V., Apáczai Csere g. I. o. t.),
Mezey Ferenc (Bp. II., Rákóczi g. II. o. t.),
Nagy Márton (Szombathely, Nagy Lajos g. I. o. t.).
‐ A könyveket postán az iskolákhoz kiküldtük.