Kezdőlap


Cím:	A talpponti háromszögről
Szerző(k):	Berkes Jenő
Füzet:	1956/március, 66 - 72. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A magasságvonalak talppontja által meghatározott háromszög, az ún. talpponti háromszög igen sok érdekes tulajdonsággal rendelkezik. Leghíresebb az a régóta ismert tulajdonsága, hogy a háromszögbe írt háromszögek közül a legkisebb kerületű (ld. a Fejér-féle bizonyítást az I. gimnáziumi tankönyvben 332 ‐ 334. old.). Háromszögszerkesztés szempontjából is sok érdekességet nyújt. Jelen dolgozatban a talpponti háromszög adatait hozzuk összefüggésbe az eredeti háromszög adataival.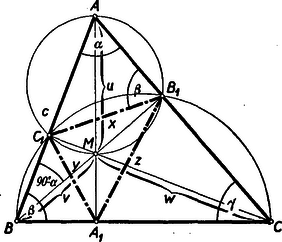
1. Egyelőre hegyesszögű háromszögről lesz szó. Jelöljük az eredeti $A B C$ háromszög szögeit $α$ , $β$ , $γ$ -val, e szögekkel szemben fekvő oldalakat $a$ , $b$ , $c$ -vel, az $A_{1} B_{1} C_{1}$ talpponti háromszögnek ezen oldalakkal szemben fekvő oldalai legyenek rendre $B_{1} C_{1} = x$ , $C_{1} A_{1} = y$ , $A_{1} B_{1} = z$ (ld. az ábrát).

B C B_{1} C_{1}

húrnégyszög, s így

\begin{matrix} A B_{1} C_{1} ∢ = A B C ∢ = β . \end{matrix}

A B C

és

A B_{1} C_{1}

háromszögek két szögben (

α

és

β

) megegyeznek, tehát hasonlóak. Következőleg

\begin{matrix} \frac{x}{a} = \frac{A B_{1}}{A B} = cos α \end{matrix}

vagyis (mindjárt felírva a hasonló képleteket

y

és

z

-re is)

\begin{matrix} x = a cos α, y = b cos β, z = c cos γ \end{matrix}

(I)

.
2. Jelöljük az

A B C_{▵}

, magassági pontját

M

-mel, és legyenek az

M A

M B

M C

szakaszok rendre

u

v

w

.
A Thales-tétel alapján az

A B_{1} M C_{1}

négyszög, valamint a

B C_{1} B_{1} C

négyszög húrnégyszög. Egy

r

sugarú kör

h (< 2 r)

húrja és a húr egyik végpontjából kiinduló átmérő által alkotott derékszögű háromszögből

\begin{matrix} h = 2 r sin ε, vagyis 2 r = \frac{h}{sin ε}, \end{matrix}

(1)

ahol

ε

a húrhoz tartozó hegyes kerületi szög.
Az

A B_{1} M C_{1}

húrnégyszög köré irt kör átmérője

M A = u

, és így a

C_{1} B_{1} = x

húrra alkalmazva az (1) összefüggést

\begin{matrix} u = \frac{x}{sin α} . \end{matrix}

(2)

(1)-hől

\begin{matrix} a = \frac{x}{cos α} \end{matrix}

(3)

(2)-t osztva (3)-mal, nyerjük, hogy

\begin{matrix} \frac{u}{a} = \frac{cos α}{sin α} = cotg α . \end{matrix}

r

-rel jelöljük az

A B C_{▵}

köré írt kör sugarát, akkor (1) alapján

a = 2 r sin α

, és így (mindjárt felírva a

v

és

w

-re adódó analóg formulákat is)

\begin{matrix} u & = a cotg α = 2 r cos α, \\ v & = b cotg β = 2 r cos β, \\ w & = c cotg γ = 2 r cos γ . \end{matrix}

3. Az

A B C_{▵}

, területe (

T

) összetevődik a

B C M

C A M

és

A B M

háromszögek területeinek összegéből. Az

A B C_{▵}

A A_{1}

B B_{1}

C C_{1}

magasságait rendre

m_{a}

m_{b}

m_{c}

-vel jelölve

\begin{matrix} a (m_{a} - u) + b (m_{b} - v) + c (m_{c} - w) = 2 T, \end{matrix}

amiből

\begin{matrix} a u + b v + c w = a m_{a} + b m_{b} + c m_{c} - 2 T = 6 T - 2 T = 4 T . \end{matrix}

Ha (II)-ből

u

v

w

értékeit behelyettesítjük, nyerjük, hogy

\begin{matrix} 2 r (a cos α + b cos β + c cos γ) = 4 T, \end{matrix}

vagyis

\begin{matrix} 2 T = r (a cos α + b cos β + c cos γ) = r (x + y + z) = r k, \end{matrix}

(III)

ahol

k

jelenti a talpponti háromszög kerületét.
Ismeretes, hogy

K

-val jelölve az

A B C_{▵}

, kerületét és

ϱ

-val a beírt kör sugarát

\begin{matrix} K ϱ = 2 T, \end{matrix}

(4)

és igy (III) és (4) egybevetéséből

\begin{matrix} k r = K ϱ, \end{matrix}

vagyis

\begin{matrix} \frac{k}{K} = \frac{ϱ}{r} . \end{matrix}

(IV)

4. A cosinus-tétel alapján

\begin{matrix} cos α = \frac{b^{2} + c^{2} - a^{2}}{2 b c} \end{matrix}

vagyis a

K = 2 s

jelölést bevezetve

\begin{matrix} 1 + cos α = 2 cos^{2} \frac{a}{2} = \frac{2 b c + b^{2} + c^{2} - a^{2}}{2 b c} = \frac{{(b + c)}^{2} - a^{2}}{2 b c} = & (5) \\ = \frac{(b + c + a) (b + c - a)}{2 b c} = \frac{2 s \cdot 2 (s - a)}{2 b c} . \end{matrix}

Innen

\begin{matrix} cos \frac{α}{2} = \sqrt[]{\frac{s (s - a)}{b c}} . \end{matrix}

Hasonlóképpen nyerjük, hogy

\begin{matrix} cos \frac{β}{2} = \sqrt[]{\frac{s (s - b)}{a c}}, cos \frac{γ}{2} = \sqrt[]{\frac{s (s - c)}{a b}} . \end{matrix}

Másrészt

\begin{matrix} 1 - cos α = 2 sin^{2} \frac{a}{2} = \frac{2 b c + a^{2} - b^{2} - c^{2}}{2 b c} = & (6) \\ \frac{a^{2} - {(b - c)}^{2}}{2 b c} = \frac{2 (s - b) 2 (s - c)}{2 b c}, \end{matrix}

ahonnan

\begin{matrix} sin \frac{α}{2} = \sqrt[]{\frac{(s - b) (s - c)}{b c}}, hasonlóképpen sin \frac{β}{2} = \sqrt[]{\frac{(s - a) (s - c)}{a c}} \\ sin \frac{γ}{2} = \sqrt[]{\frac{(s - a) (s - b)}{a b}} \end{matrix}

Mivel (1) alapján

sin γ = \frac{c}{2 r}

, igy

\begin{matrix} T = \frac{a b sin γ}{2} = \frac{a b c}{4 r}, ahonnan r = \frac{a b c}{4 T} . \end{matrix}

(7)

Tehát felhasználva Heron képletét

\begin{matrix} sin \frac{α}{2} \cdot sin \frac{β}{2} \cdot sin \frac{γ}{2} = \frac{(s - a) (s - b) (s - c)}{a b c} = \frac{T^{2}}{s a b c} = \frac{T \frac{T}{s}}{a b c}, \end{matrix}

ahonnan (4), (7) és (IV) figyelembevételével

\begin{matrix} sin \frac{α}{2} \cdot sin \frac{β}{2} \cdot sin \frac{γ}{2} = \frac{T ϱ}{4 T r} = \frac{ϱ}{4 r} = \frac{k}{4 K} . \end{matrix}

(V. 1)

(7) és (IV) felhasználásával

\begin{matrix} cos \frac{α}{2} \cdot cos \frac{β}{2} \cdot cos \frac{γ}{2} = \frac{\sqrt[]{s (s - a) (s - b) (s - c)}}{a b c} = \frac{s T}{a b c} = \frac{s}{4 r} = \frac{K}{8 r} = \frac{k}{8 ϱ} . & (V.2) \end{matrix}

(V. 1) és (V. 2) osztásából

\begin{matrix} tg \frac{α}{2} tg \frac{β}{2} tg \frac{γ}{2} = \frac{ϱ}{s} = \frac{2 ϱ}{K} . \end{matrix}

(V. 3)

5. Érdekes módon hozható kapcsolatba a talpponti háromszög oldalaival az az arány, amely a magassági pontnak a csúcstól való távolsága és az egész magasságvonal hossza között fennáll. Ugyanis

\begin{matrix} \frac{u}{m_{a}} = \frac{a cotg α}{m_{a}} = \frac{a^{2} cotg α}{a m_{a}} = \frac{\frac{a}{sin α} \cdot a cos α}{2 T} = \frac{2 r x}{2 T}, \end{matrix}

tehát

\begin{matrix} \frac{u}{m_{a}} = μ_{a} = \frac{r}{T} x, \frac{v}{m_{b}} = μ_{b} = \frac{r}{T} y, \frac{w}{m_{c}} = μ_{c} = \frac{r}{T} z, \end{matrix}

(VII)

Innen

\begin{matrix} x : y : z . \end{matrix}

Továbbá (III) figyelembevételével

\begin{matrix} μ_{a} + μ_{b} + μ_{c} = \frac{r}{T} (x + y + z) = \frac{r k}{T} = \frac{2 T}{T} = 2. \end{matrix}

Ebből nyilvánvaló, hogyha két magasságvonalon ismeretes az osztási arány, akkor a talpponti háromszöghöz hasonló talpponti háromszög, ebből pedig az eredeti hegyesszögű háromszöghöz hasonló háromszög szerkeszthető.
6. Egyébként

k

igen érdekesen fejezhető ki az

A B C_{▵}

oldalaival. (5) és (6) alapján

\begin{matrix} x = a cos α = a (cos^{2} \frac{α}{2} - sin^{2} \frac{α}{2}) = a \frac{s (s - a) - (s - b) (s - c)}{b c} = & (VIII) \\ = a \frac{b^{2} + c^{2} - a^{2}}{2 b c} = a \frac{4 s (s - a) - 2 b c}{2 b c} = \frac{2 a^{2} s (s - a) - a^{2} b c}{a b c} . \end{matrix}

A betűk ciklikus felcserélésével hasonló formulákat nyerünk

y

-ra és

z

-re, és így

\begin{matrix} k = x + y + z = \frac{2 s [a^{2} (s - a) + b^{2} (s - b) + c^{2} (s - c)] - a b c (a + b + c)}{a b c} = & (IX) \\ = \frac{2 s [a^{2} (s - a) + b^{2} (s - b) + c^{2} (s - c) - a b c]}{a b c} . \end{matrix}

Mivel

2 s = K

, azért

\begin{matrix} \frac{k}{K} = \frac{s (a^{2} + b^{2} + c^{2}) - (a^{3} + b^{3} + c^{3})}{a b c} - 1. \end{matrix}

2-vel szorozva

\begin{matrix} \frac{2 k}{k} = \frac{2 s (a^{2} + b^{2} + c^{2}) - 2 (a^{3} + b^{3} + c^{3})}{a b c} - 2, \end{matrix}

ahonnan (4) figyelembevételével

\begin{matrix} \frac{2 k}{K} + 2 = \frac{2 ϱ}{r} + 2 = \frac{(a + b + c) (a^{2} + b^{2} + c^{2}) - 2 (a^{3} + b^{3} + c^{3})}{a b c} = & (X) \\ = \frac{a b^{2} + a c^{2} + b a^{2} + b c^{2} + c a^{2} + c b^{2} - a^{3} - b^{3} - c^{3}}{a b c} = \\ = (\frac{a}{b} + \frac{a}{c} - \frac{a^{2}}{b c}) + (\frac{b}{a} + \frac{b}{c} - \frac{b^{2}}{a c}) + (\frac{c}{a} + \frac{c}{b} - \frac{c^{2}}{a b}) . \end{matrix}

Egyenlő szárú háromszög esetén, ha

a = b

, (X)-ből

\begin{matrix} \frac{2 k}{K} + 2 = \frac{2 ϱ}{r} + 2 = (1 + \frac{a}{c} - \frac{a}{c}) + (1 + \frac{a}{c} - \frac{a}{c}) + (\frac{2 c}{a} - \frac{c^{2}}{a^{2}}) \end{matrix}

ahonnan

\begin{matrix} \frac{k}{K} = \frac{ϱ}{r} = \frac{c}{a} - \frac{1}{2} \cdot \frac{c^{2}}{a^{2}} = 2 \frac{c}{2 a} - 2 {(\frac{c}{2 a^{2}})}^{2} = 2 sin \frac{γ}{2} - 2 sin^{2} \frac{γ}{2} . \end{matrix}

(XI)

7. (1) alapján

\begin{matrix} \frac{sin α + sin β + sin γ}{K} = \frac{\frac{a}{2 r} + \frac{b}{2 r} + \frac{c}{2 r}}{K} = \frac{a + b + c}{2 r K} = \frac{1}{2 r}, \end{matrix}

vagyis (IV) figyelembevételével

\begin{matrix} sin α + sin β + sin γ = \frac{K}{2 r} = = \frac{k}{2 ϱ} . \end{matrix}

(XII)

(V. 1) és (V. 2) 8-szoros szorzata

\begin{matrix} 8 sin \frac{α}{2} sin \frac{β}{2} sin \frac{γ}{2} cos \frac{α}{2} cos \frac{β}{2} cos \frac{γ}{2} = 8 \frac{k}{4 K} \cdot \frac{K}{8 r}, \end{matrix}

vagyis

\begin{matrix} sin α + sin β + sin γ = \frac{k}{4 r} . \end{matrix}

(XII) és (XIII) hányadosa

\begin{matrix} \frac{sin α + sin β + sin γ}{sin α sin β sin γ} = \frac{2 r}{ϱ}, \end{matrix}

(XIV)

8. Felhasználva a

\begin{matrix} ϱ ≦ \frac{r}{2} \end{matrix}

(8)

ismert egyenlőtlenséget (ld. jelen számunkban a 744. sz. kitűzött feladatot) (IV)-ből következik

\begin{matrix} \frac{k}{K} ≦ \frac{1}{2}, \end{matrix}

(IV')

továbbá (III) és (IV') alapján

\begin{matrix} 4 T = 2 r k ≦ 2 r \frac{K}{2} = r K, \end{matrix}

amiből

\begin{matrix} \frac{r}{4} ≧ \frac{T}{K} . \end{matrix}

(III')

Végül (XIV)-ből ‐ (8) figyelembevételével ‐ következik

\begin{matrix} sin α + sin β + sin γ ≧ 4 sin α sin β sin γ . \end{matrix}

(XIV')

A (IV'), (III'), (XIV') egyenlőtlenségekben az egyenlőség jele csak szabályos háromszög esetén érvényes.
9. Eddig tulajdonképpen csak hegyesszőgű háromszögről beszéltünk, bár több általánosan érvényes tételt felhasználtunk és levezettünk.
Derékszögű háromszög esetén a talpponti háromszög egyenessé fajul, tehát háromszögről, mint olyanról, nem beszélhetünk.
Tompaszögű háromszögre mindenekelőtt megállapítjuk, hogy ugyanahhoz a talpponti háromszöghöz mindig tartozik egy hegyesszögű és három tompaszögű háromszőg. Pl. ábránkban az

A M B

B M C

és

C M A

tompaszögű háromszögeknek ugyancsak az

A_{1} B_{1} C_{1}

, a talpponti háromszögük. Azonkívül mindhárom tompaszögű háromszög köré írt körének sugara megegyezik a

A B C_{▵}

köré írt kör

r

sugarával. (Ez következik a Vályi-féle tételből. L. 332. sz. gyakorlatot a múlt számunkban.)
Tehát az

{A_{1} B_{1} C_{1}}_{▵}

talpponti háromszöge az

u

v

c

oldalú

{B A M}_{▵}

-nek, amelynek szögei rendre

90^{\circ} - α

90^{\circ} - β

α + β

. De (3) alatt láttuk, hogy

\begin{matrix} x = u sin α = u cos (90^{\circ} - α) . \end{matrix}

Ugyanígy

\begin{matrix} y = v sin β = v cos (90^{\circ} - β) . \end{matrix}

(1)-ből

\begin{matrix} z = c cos γ = - c cos (α + β) . \end{matrix}

Tehát tompaszögű háromszög esetén a (I) képletekben a tompaszöggel szembenfekvő oldalt negatív előjellel kell venni. Ezek szerint egy

a_{1}

b_{1}

c_{1}

, oldalú és

α_{1}

β_{1}

γ_{1}

szögű háromszög talpponti háromszögének kerülete, ha

γ_{1} > 90^{\circ}

\begin{matrix} k_{1} = a_{1} cos α_{1} + b_{1} cos β_{1} - c_{1} cos γ_{1} . \end{matrix}

Amíg a talpponti háromszög kerület-képlete tompaszögű háromszög esetén megváltozik, addig az eredeti háromszőg területének (III) képlete:

\begin{matrix} 2 T_{1} = r_{1} (a_{1} cos α_{1} + b_{1} cos β_{1} + c_{1} cos γ_{1}) \end{matrix}

változatlan marad, amint azt az alábbiakban megmutatjuk.

\begin{matrix} 2 t_{A M B} = 2 t_{A B C} - 2 t_{B M C} - 2 t_{C M A} = 2 T - a (m_{a} - u) - b (m_{b} - v) = \\ = 2 T - 2 T + a u - 2 T + b v = a u + b v - 2 T = \\ = r (2 a cos α + 2 b cos β - a cos α - b cos β - c cos γ) = \\ = r (a cos α + b cos β - c cos γ) . \end{matrix}

Másrészt alkalmazzuk most a (III) képletet az

{A M B}_{▵}

-re

\begin{matrix} (a_{1}=u, b_{1}=v, c_{1} = c, α_{1} = 90^{\circ} - α, β_{1} = 90^{\circ} - β, γ_{1} = α + β r_{1} = r) \\ 2 t_{A M B} = r [u cos (90^{\circ} - α) + v cos (90^{\circ} - β) + c cos (α + β)] . \end{matrix}

(II) figyelembevételével

\begin{matrix} 2 t_{A M B} = r (a cos α + b cos β - c cos γ) . \end{matrix}

Ezzel igazoltuk állításunkat.
Nem érvényes természetesen tompaszögű háromszögre a (IV)

\begin{matrix} \frac{ϱ_{1}}{r_{1}} = \frac{k_{1}}{K_{1}} \end{matrix}

képlet. Igaz marad ugyan ‐ amint láttuk ‐ a

\begin{matrix} K_{1} ϱ_{1} = 2 T_{1} = r_{1} (a_{1} cos α_{1} + b_{1} cos β_{1} + c_{1} cos γ_{1}), \end{matrix}

azaz a

\begin{matrix} \frac{ϱ_{1}}{r_{1}} = \frac{a_{1} cos α_{1} + b_{1} cos β_{1} + c_{1} cos γ_{1}}{K_{1}} \end{matrix}

összefüggés, csakhogy most a jobboldal számlálója nem egyenlő

k_{1}

-gyel.
A többi összefüggés vizsgálatát már ezek alapján az olvasóra bízzuk.