Cím: Képek a magyar matematika múltjából VI.
Szerző(k):  Obláth Richárd 
Füzet: 1956/január, 1 - 8. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek
Hivatkozás(ok):Feladatok: 1956/január: 731. matematika feladat, 1956/március: 747. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

VÁLYI GYULA
1855. január 25.‐1913. október 13.
 

Az a magyar matematikus, akiről ma megemlékezünk, édesanyja, Dózsa Rachel révén Dózsa Györgynek, az 1514. évi parasztfelkelés nagy vezérének egyenes leszármazottja, >>késő unokája<<. Ez idén volt születésének századik évfordulója.
Marosvásárhelyen, a Bolyaiak városában született 1855. január 25-én. Bolyai Farkas1 iskolájában, a marosvásárhelyi református gimnáziumban tanult, talán a gimnázium tradíciója is vonzotta a matematikához, mert a család szoros barátságban élt Bolyai Farkassal. Iskolái végeztével mint erdélyi fiú, a csak pár évvel azelőtt alapított kolozsvári egyetemre iratkozott be, ahol a kicsi termetű, sovány, vézna fiatalember tehetségével és szorgalmával csakhamar feltűnt. Az egyetemi tanulmányok végeztével állami ösztöndíjjal Berlinbe ment. Az időben ugyanis a matematikában a berlini egyetem versenytárs nélkül állt. Olyan tanári kar volt ott együtt, aminő csak nagyot ritkán található együtt egy egyetemen. Weierstrass, Kronecker, Kummer együttesét tréfásan >>Dreigestirn<<-nek, >>hármas csillagzat<<-nak hívták, és a világ minden részéről mentek tehetséges ifjú matematikusok Berlinbe, hogy ettől a páratlan tanári testülettől tanuljanak és az egész életre szóló benyomásokat szerezzenek. Itt tökéletesítette tanulmányait az ifjú Vályi is.
De tragikuma, mely egész életét elkeserítette, már berlini tanulmányi ideje alatt, ifjú korában kezdődött. Szembaja, mely mindvégig kínozta, oly súlyossá vált, hogy hónapokon át olvasni sem tudott. Még forrón szeretett édesanyjának sem írhatott, akivel pedig addig igen sűrű levelezésben állt. Képzeljük el ezt a csapást, a tudóst, aki képtelen olvasni, a lelkes matematikust, aki nem lát. Hasonló ez a tragikum a süket zenész tragikumához, talán még súlyosabb. Ahogy Beethoven süketsége ellenére minden idők legnagyobb zenészei közül való, akadnak vak matematikusok is. Napjainkban Pontrjagin hírneves szovjet matematikus, és a XVIII. században Euler, a matematika egyik fejedelme is vak volt. Vályi ugyan nem volt teljesen vak, de véres szeme miatt olvasni nem tudott.
Ifjú olvasóink jól tudják, hogy a matematika nem valami holt dolog, mely egyszersmindenkorra készen van, hanem olyasmi, amin állandóan több ezer ember gondolkodik, amely tehát eleven, állandóan rohamosan fejlődik, gyarapodik. Ez a fejlődés oly gyors, hogy aki követni akarja, akkor is minden képességét össze kell szednie, ha jól lát, hát még milyen szellemi éberséget, emlékező tehetséget és agymunkát követel attól, aki nem lát ! Minő akaraterejének, fantáziájának és emlékezetének kell lennie, hogy pusztán hallásból tanuljon matematikát és milyen éles elméjűnek, hogy mindent első hallásra felfogjon. Vályi ezt a rendkívüli akadályt is le tudta küzdeni. Nemcsak meg tudott maradni a mindenkori tudomány legmagasabb szintjén, hanem kutató tudóssá fejlődött, aki szép és érdekes eredményekkel gazdagította tudásunkat.
1881-ben a kolozsvári egyetem magántanára lett, 1887-től pedig egyetemi tanár volt.
Mintaszerűen tökéletes, a tudomány mindenkori haladásával lépést tartó egyetemi előadásokat tartott. Sohasem ismételte ugyanazt az előadást változatlanul. Utóda, Haar Alfréd ‐ aki persze már a magyar tudomány úttörőinek munkája nyomán virágba szökkent magyar matematika kiemelkedő, világszerte ismert alakjai között foglal helyet ‐ mondta róla, hogy a függvénytant sehol sem adták elő a Vályiénál magasabb színvonalon.
Áttérek Vályi azon munkáinak ismertetésére, amelyek ifjú olvasóinkat érdekelhetik.
Az egyetemi tanulmányokat a tehetséges fiatalok azelőtt rendszerint a doktori cím megszerzésével zárták le. A doktorátus leglényegesebb követelménye egy munka, az ún. disszertáció elkészítése volt, amelynek az volt a feladata, hogy bizonyítsa a jelölt képességét, a tudomány továbbfejlesztésére. Vályi doktori disszertációja a legfelsőbb matematikához tartozik ugyan, mégis tisztán gyakorlati kérdés az eredete. A múlt század második felében igen sok embert foglalkoztatott a repülés problémája. Ifjú olvasóim között bizonyára vannak, akik olvastak néhány, ekkor keletkezett, fantasztikus regényt ‐ Jókai is írt ilyet, a >>jövő századról<<, ami persze a mi századunk, amelyben a repülés már meg lesz oldva. (Hogy a repülőgép pusztulást, atom- és hidrogénbombát hozhat, arra a regényírók egészséges érzéke persze még nem gondolt.) De nemcsak az írók, nagyapáink és dédapáink korának tudósai is lázasan kutattak a repülés lehetőségei után. A kolozsvári egyetem tanárai között is volt egy, aki a repülőgépet igyekezett feltalálni, és egyik alkatrészét a hajócsavar (= propeller) mintájára peripellernek nevezte. A matematikusok az állítólagos feltalálót nem vették komolyan, de a >>peripeller<< mozgásának törvényszerűségeit érdeklődéssel fogadták. Az ezen mozgás leírásához megoldandó matematikai problémát tanulmányozta Vályi doktori értekezése.
Az a bizonyos kolozsvári repülőgép nem vált be (csak mintegy 30 évvel később szerkesztettek oly gépet, amely tényleg repült), de a matematikai feladat érdekesebb volt a technikai találmánynál, amelyből keletkezett. Vályi problémája figyelmet keltett. A magyar matematikusok közül Kürschák foglalkozott vele, és külföldi matematikusok érdeklődését is felkeltette. Ezek egyike 25 év múlva észrevette, hogy a disszertáció utolsó oldalán számolási hiba van, amelynek kijavítása után Vályi egyik megoldatlanul maradt problémája is megoldhatóvá vált.
A doktorátus letétele után Vályit az egyetemen tartották, ahol néhány év múlva (1887-ben) rendes tanár és valamivel később (1891-ben) a Tudományos Akadémia tagja lett.
Vályi főleg az elemi és felsőbb matematika határterületein tevékenykedett. Bemutatandó eredményei is többnyire ezek közül valók.
Vályi igen sokat foglalkozott a perspektív háromszögekkel. Perspektívnek nevezünk két idomot, ha megfelelő pontjaik összekötő egyenesei ugyanazon ponton mennek át, vagyis ebből a pontból nézve egymást pontosan elfödik. (Innen van a név.) ABC és A1B1C1 háromszögek tehát perspektívek, ha az AA1, BB1, CC1 egyenesek ugyanazon S pontban találkoznak.
A perspektív háromszögek elméletének alaptételét Desargues (ejtsd Dézárg, az á rövid, 1591‐1662) francia építész találta és így szól:
Perspektív háromszögek megfelelő oldalpárjainak metszéspontjai ugyanazon egyenesen feküsznek és fordítva, ha két háromszög megfelelő oldalainak metszéspontjai egy egyenesen feküsznek, akkor a megfelelő csúcsaikat összekötő egyenesek ugyanazon ponton mennek át (vagyis a háromszögek perspektívek. (Ld. az 1. ábrát.)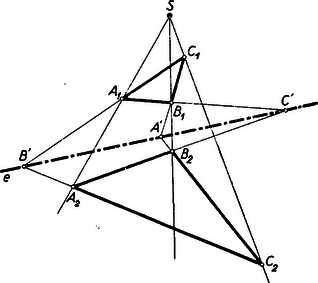
 
 
1. ábra
 

Olvasóink bizonyára tapasztalták, hogy a geometriai tételek bizonyítása könnyebb a síkban, mint a térben. Sajátságos, hogy egyes esetekben megfordul a helyzet, így Desargues tétele is az utóbbiakhoz tartozik. Desargues tétele ugyanis a térben jóformán magától értetődő, bizonyítása a síkban jóval bonyolultabb.
Csakugyan, ha a perspektív ABC és A1B1C1 háromszögek nincsenek egy síkban, akkora megfelelő csúcsok összekötésével 3 oldalú gúlát kapunk, és magától értetődik, hogy a megfelelő háromszög metszéspontjai a háromszögek síkjainak metszésvonalában, tehát egy egyenesen vannak (2. ábra).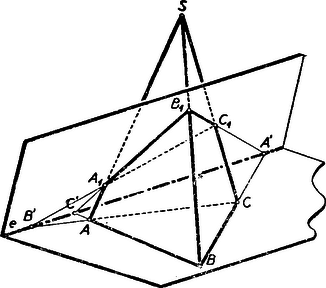
 
 
2. ábra
 

Bonyolultabb a helyzet, ha mindkét háromszög ugyanabban a síkban van. Ekkor ugyanis a két sík azonos, metszésvonaluk határozatlan, tehát az eddigi okoskodás értelmét veszti. A legegyszerűbb bizonyítás ‐ ezt azonnal bemutatjuk ‐ abban áll, hogy kivetítjük mindkét háromszöget egy vele perspektív térbeli háromszögbe és ha ügyesen járunk el, ugyanaz a térbeli háromszög lesz mindkét adott háromszöggel perspektív (3. ábra).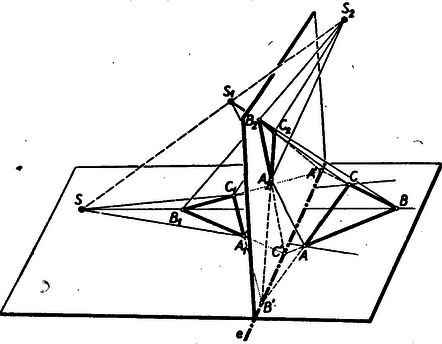
 
 
3. ábra
 

S az ABC és A1B1C1, háromszögek perspektívitása centruma. Ha ABC és A1B1C1 ugyanabban a síkban feküsznek, kössük össze a tér valamely, a háromszögek síkján kívül levő, S1 pontját az A, B, C pontokkal, és kössük össze az SS1 egyenesen tetszés szerint (de az adott háromszögek síkján kívül) felvett S2 pontot az A1, B1, C1 pontokkal. Az SA, SB, SC segédvonalak metszése rendre SA1, SB1, ill. SC1-gyel legyen A2,B2, C2, ekkor az A2B2C2▵ mind az ABC, mind az A1B1C1 háromszöggel perspektív. Az AB, A1B1, A2B2 egyenesek ugyanazon C' ponton mennek át, mert párosával egy-egy síkban vannak, és metszéspontjuk az eredeti síknak és az A2B2C2 háromszög síkjának metszésvonalán van. Ugyanúgy a BC, B1C1, B2C2 vonalak is egy A' ponton haladnak át, a CA, C1A1, C2A2 egyenesek pedig egy B' ponton. Az A', B', C' pontok az ABC és A2B2C2 síkok metszésvonalán, tehát egy egyenesen feküsznek. Q. e. d. (Quod erat demonstrandum = Ami bizonyítandó volt.)
Ha fordítva az ugyanazon síkban fekvő ABC és A1B1C1 háromszögek megfelelő oldalainak metszéspontjai A', B', C' ugyanazon e egyenesen vannak, akkor vetítsük az A1B1C1 háromszöget a tér tetszőleges S2 pontjából valamely, az e-n átmenő, tetszőleges síkra. Ha ez a vetület A2B2C2▵, akkor A2B2 átmegy az AB és A1B1 egyenesek C' metszéspontján, ugyanígy B2C2 és BC metszéspontja A', valamint C2A2 és CA metszéspontja B'. Ennélfogva AA2, BB2, CC2 párosával egy-egy síkban vannak, és egy pontjuk (a három sík metszéspontja) S1 közös. Az S1S2 egyenesnek az ABC síkkal való S metszéspontja tehát az AA1, BB1, CC1 egyenesek mindegyikén rajta van, vagyis e három egyenes ugyanabban a pontban metszi egymást, és ezzel a Desargues-tétel megfordítását is bebizonyítottuk.
A Desargues-tétel a geometria legfontosabb tételei közé tartozik, és amint Hilbert, századunk egyik legnagyobb matematikusa megmutatta, a geometria felépítésében kimagasló szerepe van, de ennek kifejtése túl messzire vezetne.
Előfordulhat az az eset is, hogy két háromszög többszörösen perspektív, amin azt értjük, hogy a két háromszög csúcsait többféleképpen lehet úgy megfeleltetni, hogy a megfelelő csúcspontok összekötő egyenesei egy pontban messék egymást. Előfordulhat pl., hogy nemcsak az A1A2, B1B2, C1C2 egyenesek metszik egymást egy S pontban, hanem pl. az A1A2, B1C2, C1B2 egyenesek is valamely S' pontban (4. ábra). Ekkor a háromszögeket kétszeresen perspektíveknek nevezzük.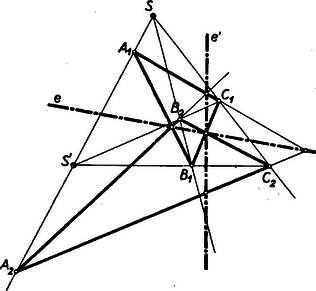
 
 
4. ábra
 

Hogy Vályi néhány idevágó eredményét elmondhassam, még egy fogalommal (illetve annak legegyszerűbb esetével) kell megismerkednünk. Tudjuk, hogy a körnek, ellipszisnek, hiperbolának, parabolának, sőt az egyenespárnak közös gyűjtőneve kúpszelet (mert ezen görbék bármelyike lehet egy körkúp síkmetszete). Valamely, a kúpszeleten kívül fekvő P pont polárisának a pontból a kúpszelethez húzható érintők érintési pontjait összekötő egyenesét nevezzük. A kúpszeletet metsző egyenesnek a kúpszeletre vonatkozó pólusa pedig: a kúpszelethez az egyenesnek a kúpszelettel való metszéspontjaiban húzott érintők metszéspontja.
Lapunk egyik legújabb számában cikket talál az olvasó, amelyben szerepel a harmonikus pontnégyes fogalma.2 A P ponton át húzott tetszés szerinti, a kúpszeletet metsző, egyenes két pontban metsz. Nevezzük a P pontnak erre a két pontra, mint alappontokra, vonatkozó harmonikus párját Q-nak. A kúpszeletek elméletének egyik alapvetően fontos tétele értelmében a Q pontok mértani helye egyenes vonal, a P pontnak a kúpszeletre vonatkozó polárisa, és viszont valamely p egyenes pontjainak polárisa egy fix P pont körül forognak. Megmutatható, hogy kívül fekvő pont, illetőleg metszőegyenes esetén ez megegyezik a fentebb definiált fogalmakkal. A P pontot a p egyenes pólusának nevezzük. Pólus és poláris tehát szorosan összefüggő fogalmak, a kapcsolat köztük kölcsönös. A most megismert értelmezésből kitűnik, hogy a kúpszelet belsejében fekvő pontnak is van polárisa. A kúpszeletet metsző egyenes pólusa tehát a kúpszeleten kívül van, mégpedig a kúpszelethez ‐ az egyenessel való metszéspontjaiban ‐ húzott érintők metszéspontja.
Vályi sokat foglalkozott a perspektív háromszögek és a pólus‐poláris kapcsolatával. 3 Ilyen tételek pl.: Két perspektív háromszöghöz mindig találhatunk oly kúpszeletet, amelyre vonatkozólag az egyik háromszög csúcsainak polárisai a másik háromszög megfelelő oldalai. Ez a vonatkozás kölcsönös. Vályi azt is bebizonyította, hogy ha a két háromszög többszörösen, pl. r-szeresen perspektív, akkor r számú ilyen kúpszelet van, kétszeres perspektivitásnál a két kapott kúpszelet egymást kétszer érinti.
Vályi számos tételt állított fel a többszörösen perspektív háromszögekről, analitikailag bizonyítja őket, de ismertetésük túl messzire vezetne. A térre is kiterjeszti vizsgálatait. Erről néhány szót szólok.
Az ABCD és A1B1C1D1, tetraéderek (háromoldalú gúlák) perspektívek, ha a megfelelő csúcsokat összekötő egyenesek (AA1, BB1, ... stb.), metszik egymást, mégpedig ugyanabban az S pontban, amelyet a perspektivitás centrumának nevezünk. Desargues tétele két perspektív tetraéderre:
Két perspektív tetraéder megfelelő élei metszik egymást, vagy párhuzamosak. A megfelelő élek síkjainak közös pontja nyilvánvalóan a perspektivitás S centruma, a megfelelő élek metszéspontjainak közös síkja a perspektivitás síkja.
Vályi Gyula Kőnig Gyulával a nagy magyar matematikussal együtt felvetette a kérdést, hogy megfordítva, pusztán abból a tényből, hogy két tetraéder élei egyáltalán metszik egymást, következik-e szükségképpen a perspektív helyzet.
Többszörösen perspektív tetraéderekkel is foglalkozik Vályi,4 de ezeket az eredményeit nem ismertethetem. Bemutatom azonban egy szép háromszög-geometriai tételét.
Ha az ABC háromszög magassági pontja M és a BCM, CAM, ABM háromszögek köré írt körök középpontjai A1, B1, C1, akkor az ABC és A1B1C1 háromszögek egybevágók.
Ezzel kapcsolatban bizonyítható, hogy az ABC▵ magassági pontja M egyszersmind az A1B1C1 köré írt kör középpontja és viszont az ABC▵ köré írt kör középpontja az A1B1C1▵ magassági pontja.
Egyszerű bizonyítást adott Vályi a következő érdekes feladatra is.5 Határozzuk meg az összes olyan háromszögeket, amelyeknek oldalait egész számok, kerületét és területét pedig ugyanaz a számérték méri.
Vályi megoldása lényegében a következő:
Legyenek az oldalak, a, b, c; a kerület a+b+c=2s és vezessük be az
s1=s-a;s2=s-b;s3=s-c
jelöléseket. Ekkor, ha t a terület, Heron képlete szerint
t2=ss1s2s3(1)
csak úgy lehet egész szám, ha mindegyik tényező egész szám, mert ellenkező esetben s és vele együtt a többi tényező is páratlan szám fele volna, s így szorzatuk számlálója páratlan, nevezője pedig páros lenne.
A feladat feltétele szerint t=2s. Ezt (1)-be helyettesítve, s-sel egyszerűsítve, és figyelembe véve, hogy
s1+s2+s3=3s-2s=s,
kapjuk, hogy
4(s1+s2+s3)=s1s2s3(2)

Ezt s3-mal szorozva, így alakíthatjuk át:
4s32=s1s2s32-4s1s3-4s2s3=(s1s3-4)(s2s3-4)-16,
azaz
(s1s3-4)(s2s3-4)=4(s32+4).(3)
Ebből kiolvasható, hogy s1≠s2, mert különben a baloldalon négyzetszám állna, a jobboldal viszont csak úgy lehetne négyzetszám, ha s32+4 is teljes négyzet lenne; ha azonban tényleg háromszögről van szó, akkor s3 nem lehet nulla, ezért s32+4 nem lehet teljes négyzet. Mivel az összefüggés [a (2) alakban] s1, s2, s3-ban teljesen szimmetrikus, azért a három szám között nem lehet két egyenlő. Az általánosság megszorítása nélkül feltehető, hogy
s1>s2>s3.(4)
Ekkor (2)-ből
s1s2s3<12s1azazs2s3<12.

Itt s3<s2 folytán s3<4, de s3=3 sem lehet, mert akkor s2 legalább 4 volna és így szorzatuk legalább 12 lenne. Így csak s3=1 és s3=2 lehet. Ezeket az értékeket (3)-ba behelyettesítve, ha s3=1, akkor
(s1-4)(s2-4)=20.
Így s1 és s2(<s1) lehetséges értékei
s1:MM24,MM14,MM9,s2:5,6,8.
Ha s3=2, akkor (3)-ból, 4-gyel egyszerűsítve
(s1-2)(s2-2)=8,
így a lehetséges értékek
s1:MM10,MM6,s2:3,4.
Mindezek, kielégítik (4)-et. Így a feltételnek a következő oldalhosszúságú háromszögek felelnek meg:
s1M24MM14MM9MM10MM6Ms25M6M8M3M4Ms31M1M1M2M2Ms30M21M18M15M12Ma6M7M9M5M6Mb25M15M10M12M8Mc29M20M17M13M10M

Vályi következő problémája is érdekelheti olvasóinkat:
Vegyünk egy háromszöget, azután a magassági talppontokkal alkotott háromszöget, azután ezen talpponti háromszög magassági talppontjainak háromszögét és így tovább. Melyek azok a háromszögek, amelyeknél ez az eljárás (véges számú lépésben) a kiinduló háromszöghöz hasonló háromszögre vezet ? Vagyis, melyek azok a háromszögek, amelyek n-edik talpponti háromszöge hasonló az eredetihez ? A feladat érdekessége az, hogy ennek a látszólag tisztán geometriai kérdésnek a megoldása is számelméleti (oszthatósági) feladatra vezet. A megoldás részleteire nem térhetünk ki.6
Nem szándékom Vályi többi munkáját ismertetni,7 hiszen a legtöbb meghaladja a középiskolai matematika színvonalát.
Említettem már egyetemi előadásait, amelyekbe számos saját eredményét is beolvasztotta. Előadásainak ezért nagy részük van abban, hogy Vályi Gyulát ma is a magyar matematika büszkeségei közé számítjuk. Rendkívüli gondot fordított rájuk és állandó csiszolásukra. Természetesen előadásaiban is emlékezőtehetségére volt utalva. Villámcsapásként érte ezért, amidőn egyszer előadás közben emlékezete cserben hagyta. Korlátlan kétségbeesésében azonnal nyugdíjazását kérte, pedig nem volt öreg, szó sem lehetett általános emlékezetgyengülésről, csak pillanatnyi emlékezetkiesésről, ami fiatal emberekkel is megtörténhetik, és amit senki sem szégyell. Kartársai mindenképpen igyekeztek szándékáról lebeszélni, de ő hajthatatlan maradt. Ő, a lelkes, tanár, aki jelentékeny egyéniségének legszebb értékeit a tanári katedrán mutatta meg, túlzott lelkiismeretességében maga hajszolta keresztül nyugdíjazását. Nyugdíjas korában szeme tovább romlott; nem sokáig volt nyugdíjas, 1913. október 13-án, 59 éves korának betöltése előtt meghalt, de a magyar matematika történetében maradandó nevet biztosított magának.
1A Bolyaiak, az apa Farkas és még nagyobb fia, János a magyar matematika örök dicsőségei. Ifjú olvasóink bizonyára hallottak már róluk. Bolyai János elsőnek épített fel egy, párhuzamosak axiómájától független geometriai rendszert. Lapunk már többször megemlékezett mindkettőjükről. Ld. a következő cikkeket: Obláth R.: Fiatal matematikusokról, lapunk IV, kötete, (1952) 97‐110. old. (főleg 103‐104.). Kárteszi F.: Bolyai János, lapunk V. kötete, (1952) 65‐75. old., ahol bővebb ismertetés található.

2Kárteszi Ferenc: A Menelaus és a Ceva-féle tétel c. cikk 4. fejezete: A harmonikus pontnégyes. Lapunk XI. Kötet, 3‐4. szám, 1955 november, 74‐75. old.

3Többszörösen kollineár háromszögek kúpszeleteknél. Math. Term. Tud. Ért. 2., 1884. 170‐174. old.
Németül: Mehrfach collineare Dreiecke bei Kegelschnitten. Math. und natw. Ber. aus Ungarn 2., 1884., 232‐236. old és Mehrfache Collineation von zwei Dreiecken. Archiv d. Math. u. Phys. 70. kötet, 1883, 105‐110. old. és (2) sorozat 2 kötet (1885) 320. old.
Többszörösen perspektív háromszögek a síkban. Math. és Phys. Lapok 7., 1898., 105‐114. old.
Németül: Monatshefte für Math. u. Phys. 9., 1898.
Többszörös polárreciprocitás a síkban. Math. Term. Tud. Ért. 15., 1898., 399‐406. old.
Németül: Über mehrfache Polarreciprocitäten in der Ebene. Math, und natw. Ber aus Ungarn. 16. kötet, 1899., 50‐58. old.

4Többszörösen perspektív tetraéderek. Math. Term. Tud. Ért. 4., 1886. 6‐8. old.
Németül: Mehrfach perspective Tetraéder. Zur Lehre der perspectiven Tetraeder. Math. und natw. Ber aus Ungarn. 4, 1886., 1‐6. old.
A perspektív tetraéderek tanához. Math. Term Tud. Ért. 4:, 1886., 55‐56. old.
Németül Arch. d. Math. u. Phys. (2) sorozat 6. kötet, 1886.
Desargues tantételének térbeli analogonjáról. Math. Term. Tud. Ért. 11., 1893., 30‐44. old., részletesebben, Math. Phys. Lapok 3., 1894, 264‐ 273. old.
Németül: Über das räumliche Analogon des Desargues-schen Satzes, Math. und natw Ber. aus Ungarn 13., 1897. 166─182. old és Monatshefte für Mathematik und Physik 4., 1893.

5Számelméleti probléma a geometriában. Math. Phys. Lapok. 1., 1892. 56‐57. old.

6A talpponti háromszögekről. Math. Phys. Lapok 10., 1901., 309‐321. old.
Németül Über die Fusspunktdreiecke. Monatshefte für Math. Phys. 14., 1903., 243‐252, old.

7Ifjú olvasóinkat érdekelhetik még Vályi következő dolgozatai: Egy számelméleti tantétel. Math. Phys. Lapok 16., 1907., 273‐276. old.
Számelméleti apróságok. Math. Phys. Lapok 21., 1912. 296‐297. old.