Cím: Az 1962. évi Eötvös Loránd fizikai verseny
Füzet: 1963/január, 33 - 38. oldal  PDF  |  MathML 
Témakör(ök): Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat szeptember 29-én rendezte ez évi Eötvös Loránd fizikai versenyét Budapesten és 6 vidéki városban az idén érettségizettek számára. A versenyzők 5 óráig dolgozhattak, és bármilyen segédeszközt használhattak. Az alábbiakban ismertetjük a verseny feladatait és azok megoldását.

 

1. Három darab R=5cm rádiuszú, Q=1kp súlyú golyó lóg egy-egy l=7,5cm hosszú fonálon. Mindhárom fonál közös pontban van felfüggesztve. A három egymásnak támaszkodó golyóra középen r=2,5cm rádiuszú golyót helyezünk. Legfeljebb mennyi lehet ennek a golyónak a súlya (q), hogy át ne essen a három lógó golyó között ? Súrlódás nincs.
(Bártfai Tamás)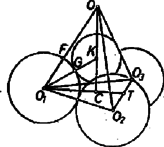
 

 
 
1. ábra
 

Megoldás. Először tekintsük át a geometriai viszonyokat (1. ábra). A nagy golyók középpontjai szabályos háromszöget alkotnak, amelynek mindegyik oldala 2R hosszúságú. A háromszög magassága O1T=R3. A gömböket tartó fonalak szabályos háromszög alapú egyenes gúla oldalélei. E gúla oldalélei O1F+FO=R+l hosszúságúak. A gúla OC térbeli magassága az alaplap O1T magasságát O1-től az alaplap magasságának 2/3-ában éri, ezért O1C=233⋅R. A kis golyó K középpontja a térbeli magasságon van. 2. ábránk az O1TO függőleges metszetet tünteti fel. O1K=O1G+GK=R+r.
 
 
2. ábra
 

Minden geometriai méret kiszámítható, például a kis golyó középpontjának a magassága a három nagy golyó középpontjainak síkja felett:
a=(R+r)2-(233R)2.
A kis golyó középpontjának a felfüggesztési ponttól mért KO távolsága:
b=(R+l)2-(233R)2-(R+r)2-(233R)2.
Olyan golyó, amelynek r rádiusza kisebb, mint (233-1)R, a súlyra való tekintet nélkül átesik a három nagy golyó közötti lyukon. Az O1F rádiusz és az l=FO fonál feltétlenül egy egyenesbe esik, ha nincs súrlódás, mert ha ez nem így volna, akkor az O1 gömb középpontja magasabbra kerülne, mint O2 és O3 középpontjai.
A feladat megoldható a következő alapon: ha a három nagy golyó még összeér, de már nem nyomja egymást, akkor a nagy golyó Q súlyának és a kis golyó súlyától származó erőnek az eredője a nagy golyót tartó fonál meghosszabbításába esik. A kis golyó q súlyának harmadrésze jut az egyik nagy golyóra; ebből O1K irányában EO1 erő származik, amely Q-val összegezve adja a fonál irányában ható AO1 eredőt. EO1D△ és ABQ△ háromszögek egybevágók, az ED=BQ erő is q/3. A szerkesztésből, a szögek egyenlőségéből következik, hogy az erőkből álló ABQO1 idom a belerajzolt AQ oldallal együtt hasonló a távolságokból álló O1CKO idomhoz a benne levő O1K távolságot beleértve. A hasonlóságból következik ez az aránypár: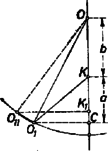
q3:Q=a:b.Innenq=3Q⋅ab.
Ez az egyenlőség adja meg a feladat megoldását. A golyók súlyából származó erők eredője abban az esetben esik a tartófonál meghosszabbításába, ha a kis golyó q súlya eleget tesz ennek a feltételnek. Ha a kis golyó súlya ennél nagyobb, akkor az eredő kifelé tolja a nagy golyót, és megindul a kis golyó átesése.
 
 
3. ábra
 

Tehát ismerjük annak feltételét, hogy mikor kezdi a kis golyó a három nagyot széttolni. Azonban egy körülményt még meg kell vizsgálni: ha a kis golyó súlya túllépi a 3Qa/b feltétel által megszabott értéket, és megindul a nagy golyók szétnyílása, vajon folytatódik-e ez a folyamat mindaddig, amíg a kis golyó átesik, és nem áll-e be útközben egy újabb egyensúlyállapot? A nagy golyók szétnyílása közben K függőleges egyenesen lefelé, O1 pedig R+l rádiuszú köríven kifelé mozog, miközben O1K=R+r állandó marad (3. ábra). Az egész mozgás lehetséges terjedelme O1 és K kezdeti állapotoktól addig az O11 és K1 állapotokig tart, amikor az R+r távolság vízszintes. Ugyanis ezután feltétlenül átesik a kis golyó. Az ábráról látható, hogy a nagy golyó felemelkedése közben C emelkedik, K pedig süllyed. Ez a csökkenését és b növekedését jelenti. Tehát az a/b tört feltétlenül kisebb lesz, ha a nagy golyók felemelkednek. Vagyis ilyenkor csak kisebb q súlyok mellett lehetséges az egyensúly, mint elinduláskor. Ebből következik, hogy későbbi egyensúlyállapot nem következhet be, és ha a kis golyó súlya eléri, illetve túllépi a 3Qa/b értéket, akkor feltétlenül szétnyomja a három nagy golyót, és teljesen átesik.
Feladatunk számadatai mellett a=4,78 cm, b=6,30 cm, a/b=0,759, és az egyensúly határesetében q=2,276 kp. Ennél nagyobb súly esetében a kis golyó átesik.
A feladat egy érdekes esetre úgy szól, hogy három léggömb lóg egyenlő hosszú fonalakon, és mindegyikük felhajtóereje Q kp. Kérdés, mekkora súlyú lehet legfeljebb az a r rádiuszú golyó, amelyet a három léggömb tetejére helyezünk, ha nem akarjuk, hogy ez a golyó átessen a három lebegő léggömb között ? (4. ábra).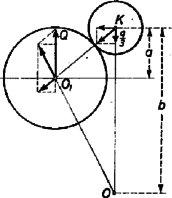
 
 
4. ábra
 

Az egyensúly feltételét ismét az jelenti, hogy a nagy gömböt felemelő erő és a kis gömb súlyából származó erő eredője a fonál irányába esik. A hasonló idomokat itt is megtaláljuk, és az egyensúly feltétele
q=3Q⋅ab.
a és b a kis golyó K középpontjától mért távolságokat jelentik:
a=(R+r)2-(233R)2,b=(R+l)2-(233R)2++(R+r)2-(233R)2.
K lefelé haladásakor a is, b is kisebb lesz, ezért nem tekinthető át olyan könnyen a/b értékének alakulása. Három eset lehetséges. Ha R+r<R+l, akkor a kis golyó süllyedésekor a/b csökken, tehát ha a kis golyó súlya túllépi a 3Qa/b határt, akkor végérvényesen lefelé halad, és újabb egyensúlyállapot nem következik be. Ha R+r=R+l, akkor K minden helyzete mellett a/b=0,5, és elérve a q=1,5Q terhelést a kis golyó bármely lenyomódott helyzetben is egyensúlyban marad, (de hamarosan megtámaszkodik az O ponton). Ha R+r>R+l, akkor a 3Qa/b terhelést túllépve a golyók megmaradnak szétnyíltan stabilis egyensúlyi helyzetben. Ez a kísérlet addig folytatható, amíg a felső golyó, az r rádiuszú azelőtt kicsiny, most nagyobb golyó meg nem támaszkodik O ponton.
 

2. Egyenletes vastagságú, azonos anyagú bádoglemezből három üres egyenes körhenger készült. Az első átmérője 5cm, magassága 5cm; a második átmérője 10cm, magassága 5cm; a harmadik átmérője 5cm, magassága 7,5cm. Megvizsgáljuk a hengerek elektromos ellenállását olyan módon, hogy a mérőműszer huzalvégeit a hengerek alap és fedő körlapjainak középpontjaihoz érintjük. Melyik henger ellenállása a legnagyobb és melyiké a legkisebb ?
(Károlyházi Frigyes)
 

 
 
5. ábra
 

Megoldás. Mindegyik esetében egy-egy elektron a bevezetés helyétől a rádiusz mentén halad az alapkör kerületéig, azután alkotó mentén megy végig a paláston, és a másik körlap rádiusza mentén éri el a kivezető drótot (5. ábra). Tehát egy-egy körlap és a hengerpalást sorba vannak kapcsolva. A nehézséget a körlap ellenállásának a kiszámítása jelenti, hiszen itt a keresztmetszet állandóan nagyobbodik. Tekintve a bádoglemez állandó vastagságát, ezt a vastagságot és a fajlagos ellenállást egyetlen arányossági szorzóban egyesíthetjük, és keresztmetszetként a rádiuszra merőleges köröket tekinthetjük. Tovább nehezíti a kérdést, hogy pontszerű bevezetés esetében a körlap ellenállása végtelen nagy volna. A feladat szövegéből az következik, hogy az áram be- és kivezetése mindegyik körnél egyforma módon, tehát ugyanakkora felületű érintkező vezetővel történik. A feladat csak azt kívánja, hogy nagyság szerint állítsuk sorba ezt a három vezetőt, ezért úgy kell eljárnunk, hogy az ellenállás pontosan meg nem határozott, de mindhárom vezetőnél egyező elemeit mint közös hozzáadandó mennyiséget vesszük tekintetbe.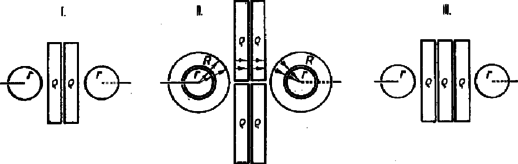
 
 
6. ábra
 

Bontsuk mindhárom vezető felületét részekre (6. ábra). Az I. henger sorba-kapcsolt két kicsiny körből és két ϱ ellenállású téglalapból áll. A II. henger esetében az áram először 2,5 cm rádiuszú kis körlapon, azután R rádiuszú körgyűrűn, majd négy ϱ ellenállású téglalapból összeállított szerkezeten, végül ismét az R ellenállású körgyűrűn és a kis körön megy végig. A harmadik henger kiterítve, sorbakapcsolt két kis körből és három téglalapból áll. Azonnal látható, hogy a III. henger ellenállása nagyobb, mint az I. hengeré, de hátra van a II. henger ellenállásának megbecsülése. A középső hengernél először sorbakapcsolt 2 téglalap, azután két ilyen kettős téglalap párhuzamosan kapcsolva egyetlen téglalap ϱ ellenállását jelenti. Ennek alapján mindegyik hengerből elveszünk egy ϱ ellenállású téglalapot (a középsőnél négyet), és elvesszük a két kis kört a bevezetésekkel együtt. (7. ábra.)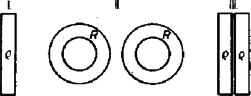
 
 
7. ábra
 


Az ezután megmaradt vezetők ellenállásai ugyanolyan nagyságbeli sorrendet alkotnak, mint az eredeti hengerek. Az I. hengerből egyetlen téglalap, a II. hengerből két körgyűrű maradt. Ezeket hasonlítjuk össze. A két sorba kapcsolt körgyűrű a vezető hosszának megkétszereződését jelenti, amit csak a keresztmetszet megkétszereződése egyenlíthetne ki. De a keresztmetszet csak kívül, a körgyűrű külső kerületén kétszeres, a beljebb fekvő körök mentén már nem, ezért biztos, hogy a két sorba kapcsolt körgyűrű nagyobb ellenállást jelent, mint egyetlen téglalap, és I.<II. Ami a II. és III. vezetőt illeti, elég egyetlen körgyűrűt és téglalapot összehasonlítanunk, hiszen 2R és 2ϱ ellenállások nagyságviszonyáról van szó. A körgyűrű és a téglalap egyenlő hosszúságú vezetőket jelentenek, tehát a keresztmetszet lesz a döntő. A téglalap hosszabbik oldala a körgyűrű belső, kisebb kerületű körének kerületével egyenlő, ehhez képest a körgyűrű kifelé nagyobb keresztmetszetűvé válik. Tehát biztos, hogy egy körgyűrű kisebb ellenállású, mint egy téglalap: R<ϱ. Ez azt jelenti, hogy a II. henger kisebb ellenállású, mint a III.: II.<III. Végeredményben a három vezető ellenállása a feladatban szereplő sorrendben következik egymás után:
I.<II.<III.  
 

3. Tőlünk 400 méterre 1 méter átmérőjű kör alakú üvegablak van, amely a róla visszaverődő napsugaraktól megcsillan. Legfeljebb meddig tart ez a jelenség?
(Vermes Miklós)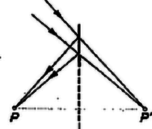

 
 
8. ábra
 

Megoldás. Az ablak megcsillanásának az a feltétele, hogy a Napról visszaverődő fénysugarak a megfigyelő szemébe essenek. A valójában P-ben levő megfigyelőt helyettesítsük P'-ben levő tükörképével, ekkor a megcsillanás feltételét az jelenti, hogy P'-ben elhelyezkedve az 1 méter átmérőjű kerek ablakon át láthatjuk-e a napkorong valamely pontját (8. ábra). Helyzetünktől függően a kerek ablakot ellipszis alakúnak látjuk, ennek a nagytengelye feltétlenül 1 méter hosszú, 400 méter távolságból nézve az 1 méteres távolságot, ezt 1/400radián=8,6 szögperc nagyságú látószögben látjuk. A Nap látószöge 30 szögperc, amint az átmérőjéből és távolságából könnyűszerrel kiszámítható. A megcsillanás lehető leghosszabb időtartamát akkor kapjuk, ha a Nap látszólagos mozgása folyamán úgy halad (illetve olyan az ablak helyzete), hogy a Nap középpontja az ellipszis alakúnak látszó ablak nagytengelyének egyenesében mozog (9. ábra). A megcsillanás addig tart, amíg a Nap 8,6+30=38,6 szögpercet tesz meg.
 

 
 
9. ábra
 

A Nap látszólagos mozgásának szögsebessége abból számítható, hogy delelései között 24óra=86400 sec telik el. Ha a Nap az égi egyenlítőn van (március 21. és szeptember 21.), akkor a talppontunktól a Napig vezető rádiusz ezalatt 360∘=21600 szögpercnyi szöget ír le, amiből 86400:21600=0,25szögpercsec mozgási sebesség következik (10. ábra).
 
 
10. ábra
 

De a Nap nincs mindig az égi egyenlítőn. A Nap június 21-én és december 21-én van legtávolabb, 23∘-nyira az égi egyenlítőtől. Ekkor 24 óra alatt nem a 2πR hosszúságú égi egyenlítőn, hanem csak a 2πr hosszúságú szélességi körön fut végig. Ezért ilyenkor a Naphoz vezető rádiusz r/R=cos23∘ arányában kisebb szögsebességgel mozog: 0,25⋅cos23∘=0,25⋅0,92=0,23szögpercsec. Ez a Nap lehetséges legkisebb szögsebessége, tehát ha a megcsillanás lehető leghosszabb idejét keressük, akkor ezzel kell számolnunk: 38,6:0,23=167,8sec=2perc47,8sec.
 

A verseny eredménye: I. díjat nyert Nagy Dénes Lajos és Szegi András (mindketten a budapesti II. Rákóczi Ferenc gimnáziumban Lantosy Károly tanítványai), III. díjat nyert Máté Eörs (a szegedi Radnóti Miklós gimnáziumban Bábitzkyné Gremsperger Katalin tanítványa). Első dicséretet kapott Góth László (a budapesti Könyves Kálmán gimnáziumban Turtóczky Sándor tanítványa), második dicséretet kapott Simonovits Miklós (a budapesti Radnóti Miklós gimnáziumban Borszéki Erzsébet tanítványa).