Kezdőlap


Cím:	Számítástechnika rovat
Szerző(k):	Ada-Winter Péter
Füzet:	1979/január, 24 - 27. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

(Rovatvezető: Ada-Winter Péter)

Feladatmegoldás

Az arany-egészek

(az 1978. októberben kitűzött feladatok megoldása)

Az aranymetszés egyenlete az

\begin{matrix} a : 1 = 1 : (1 + a) \end{matrix}

(1)

másodfokú egyenlet, amelynek ‐ mint láttuk ‐ csak egy pozitív gyöke van. Ezt mértük fel egy egységnyi oldalú négyzetrács

Q

csúcsából az egyik oldalra, így kaptuk az

U

pontot, amelyet a

Q

-val szomszédos

V

csúccsal kötöttünk össze. (1. ábra.) Az új egyenesnek a rács egyeneseiből kimetszett oldalait aranymetszés származékoknak neveztük. (Nem keletkeznek újabb távolságok, ha új egyenesünket a rács oldalaira tükrözve abból egy rombusz-hálót alakítunk ki, ezért elég az eredeti egyenest vizsgálni.) A

Q U V

háromszöget a

V

csúcsából tetszőlegesen pozitív egész

n

mellett az

n

-szeresére nagyítva az új háromszög

Q V

-vel párhuzamos oldalának hossza

n \cdot a

lesz, és helyzetét tekintve ez az oldal aranymetszés-származék. Az új befogó egyenesén levő egyéb származékok hossza ettől csak egy egész számban térhet el, nagysága tehát

n \cdot a + m

, ahol

m

és

n

tetszőleges egész szám. Hasonló eredményre vezet a

T V W

háromszög nagyítása, ahol

T

Q U V

háromszöget tartalmazó négyzet

V

-vel szomszédos csúcsa.

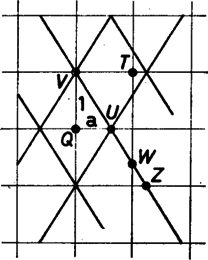1. ábra

m

pozitív, készen vagyunk, hiszen

a

-nak

n

első hatványát és

m

nulladik hatványát kell vennünk. Ha

m

negatív,

n + m > 0

, hiszen

a < 1

és

n \cdot a + m > 0

. Emiatt

\begin{matrix} n \cdot a + m = (n + m) \cdot a + m \cdot (1 - a) = (n + 2 m) \cdot (1 - a) + (n + m) \cdot (2 \cdot a - 1) . \end{matrix}

Itt (1) alapján

\begin{matrix} 1 - a = a^{2}, \end{matrix}

(2)

amiből

a

-val szorozva kapjuk, hogy

\begin{matrix} a - a^{2} = a^{3} . \end{matrix}

(3)

Mivel

a^{2} = 1 - a

, ebből

a - a^{2} = 2 a - 1

következik, tehát

\begin{matrix} n \cdot a + m = (n + m) a^{3} + (n + 2 m) a^{2} . \end{matrix}

Ha itt

n + 2 \cdot m

pozitív, készen vagyunk. Ha nem, megismételjük az eljárást mindaddig, amíg mindkét együttható pozitív nem lesz. Mivel közben az együtthatók abszolút értékben monoton fogynak, az eljárás nem lehet végtelen. Mivel pozitív számból indultunk ki, az első együttható végig pozitív marad. Előfordulhat, hogy

n

negatív és

m

pozitív (de az összeg változatlanul pozitív), ekkor az

\begin{matrix} m + n \cdot a = (n + m) \cdot a + m \cdot a^{2} \end{matrix}

átalakítás pozitív

n + m

esetén megoldja, negatív

n + m

esetén az előző esetre vezeti vissza a feladatot.
A bizonyítás közben kapott (2) összefüggés szerint

b = a^{2}

, ebből (3) alapján

c = a^{3}

következik. Hasonlóan tovább menve lépésről lépésre kapjuk, hogy a

b = 1 - a

;

c = a - b

;

d = b - c

;

...

stb. sorozat elemei

a

hatványai. Mivel az

A = 1 + a

számra az

\begin{matrix} (A - 1) : 1 = 1 : A \end{matrix}

(4)

egyenlet teljesül, ebből beláthatjuk, hogy a

B = 1 + A

;

C = A + B

;

B = B + C

;

...

stb. sorozat elemei

A

hatványai. Mivel

A = 1 + a

, a két sorozat elemei könnyen átszámolhatók egymásba. Nevezetesen az 1. feladatban mondott összefüggés azért igaz, mert

d + e = c

, így

\begin{matrix} 2 b + c + d + e = 2 (b + c) = 2 a . \end{matrix}

Emiatt

\begin{matrix} 2 = 2 a + 2 b = 4 b + c + d + e = 5 b + e . \end{matrix}

Ha általában a

{\sum_{i = - N}^{N}}_{}^{} c_{i} a^{i}

alakú számokat (ahol

| c_{i} | \leq K

egész szám) arany-egészeknek nevezünk alkalmas

K

és

N

mellett, nyilván minden aranymetszet-származék arany-egész. Két arany-egész szorzata úgy állítható elő, ahogy polinomokat szorzunk össze:

\begin{matrix} ({\sum_{i = - N}^{N}}_{}^{} c_{i} a^{i}) \cdot ({\sum_{i = - N}^{N}}_{}^{} d_{i} a^{i}) = {\sum_{i = - 2 N}^{2 N}}_{}^{} e_{i} a^{i}, \end{matrix}

ahol

i \geq 0

mellett

\begin{matrix} e_{i} = c_{- N} d_{i - N} + c_{N + 1} d_{i - N + 1} + ... + c_{i - N} d_{N}, \end{matrix}

ha pedig

i - < 0

, akkor

\begin{matrix} e_{i} = c_{- N} d_{i + N} + c_{- N + 1} d_{i + N - 1} + ... + c_{i + N} d_{- N} . \end{matrix}

Ha a

c_{i}

d_{i}

együtthatók nem negatívak, akkor az

e_{i}

együtthatók sem lehetnek negatívak, emiatt két aranymetszés-származék szorzata valóban előállítható

a

véges sok tetszőleges előjelű, egész kitevőjű hatványa összegeként. Felvethető a kérdés, nem lehetne-e ebben az előállításban az azonos kitevőjű hatványok ismétlődését elkerülni. Ha ez sikerülne, minden arany-egésznek egy kettes számrendszerben felírt számot feleltethetnénk meg, a

\begin{matrix} {\sum_{i = - N}^{N}}_{}^{} c_{i} a^{i} számnak  a {\sum_{i = - N}^{N}}_{}^{} c_{i} 2^{N + i} számot . \end{matrix}

Ezt az alakot nevezzük kanonikus alaknak, pozitív arany-egész kanonikus alakjában mindegyik

c_{i}

vagy 0, vagy 1, negatívokéban

c_{i}

értéke vagy 0, vagy

- 1

.
Nevezzük elemi műveletnek

a

valamely hatványának egy kanonikus alakú arany-egészhez való hozzáadását, vagy abból való kivonását. A megfelelő szubrutinnak ‐ CSEPP-nek neveztük el ‐ két bemenő változója van: az arany-egészeket tartalmazó tömb, és a hozzáadandó

a

hatvány

N

-nel megnövelt kitevője, ha ezt az arany-egészhez hozzá kell adni, különben annak a (

- 1

)-szerese. A túlcsordulás ellenőrzése kedvéért az első és a két utolsó együttható már nem használható fel a szám ábrázolásához, és a műveletsorok pontosságának a növelése kedvéért az elemi műveletet kétszeres méretben végezzük el. Ennek a rutinnak a megírását új feladatnak tűzzük ki. Az októberi kitűzésben meghatározott IDENT, ADD, MULT, RED, KONV szubrutinokat a megoldóknak megküldjük.

Feladat

Sz. 7. A 2. ábrán látható nyolc pontos gráfnak a bemeneti pontjától a kimeneti pontja felé úgy szabad haladni, hogy egy csomópontot csak egyszer érintsünk. A gráfba való belépés előtt kártyáról értéket kap egy

X

valós típusú változó, amely a gráf minden egyes pontjában az ahhoz rendelt függvény szerint értékét megváltoztatja. (A függvények

X = A⋇X⋇⋇2+ B⋇X + +C

típusúak.)

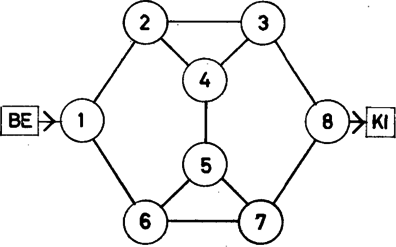2. ábra

a) Program írandó, amely

‐ megkeresi

- 10 \leq X \leq 10

azon bemenő értékét és egy hozzá tartozó

olyan utat, melynél X kimenő értéke abszolút értékben maximális;
‐ kinyomtatja X bemenő és kimenő értékeit, valamint az úthoz tartozó

pontok 2. ábra szerinti sorszámát balról jobbra haladó sorrendben;
‐ adottnak tekinti a FUNCTION FF(X, M) szubrutint, amely X-et

1 \leq M \leq 8

egész szám értékei szerint (az ábra pontjait jelző szám)

átalakítja;
‐ figyelembe veszi, hogy X-et egy kártya első pozícióiról F5.2 specifikációval

olvassuk be.

b) Hogyan módosítaná a programot, ha minden ponton legfeljebb kétszer szabadna áthaladni.

Kérjük a programot P18 azonosítóval megnevezni.

Gyakorlat (kezdők részére)

Sz. 8. Szubrutin készítendő KPS1 azonosítóval, amely egy A vektorban rendezetlenül meglevő

2 \leq n \leq 30

darab valós típusú számot az X vektor első

n

komponensébe növekvő sorrendben rendezetten elhelyezi. Nyomtatandók F8.2 specifikációval a rendezetlen és rendezett vektorok komponensei.
A feladat különféle módszerekkel oldható meg. Aki több megoldást készít, az próbálja értékelni azokat gépidő-felhasználás szempontjából.

Beküldési határidő: 1979. március 10.

HELYESBÍTÉS! A decemberi számban a februári szakkör időpontja hibásan jelent meg. A helyes időpont: február 28. du. fél 5 ‐ 7-ig.

(Könyvismertetés)

Daniel D. McCracken: Bevezetés a FORTRAN IV. programozásba (Számítástechnikai Oktató Központ, Budapest, 1970.) A FORTRAN programozási nyelv érthető, könnyen megragadható ismertetését és számos műszaki-matematikai alkalmazási példát találhat ebben az olvasó. A feladatok matematikai igényessége nem túl magas, de a könyv legnagyobb erénye a programtechnikai módszerek, fogások bemutatásában van.
Ajánlani azok részére tudjuk, akik már a kezdő fokon túljutottak, és akik szakmai igényességgel kívánják a FORTRAN programozást megtanulni.