Cím: A 2004. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldásai
Szerző(k):  Fleiner Tamás 
Füzet: 2005/február, 67 - 71. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd), Matematika, Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Adott a síkban az ABC háromszög, melynek körülírt körét kívülről érinti a k kör. A k kör érinti egyúttal az AB és AC félegyeneseket is, mégpedig a P, illetve Q pontban. Mutassuk meg, hogy a PQ szakasz felezőpontja egybeesik az ABC háromszög BC oldalához hozzáírt körének középpontjával.

 

I. megoldás. Alkalmazzunk inverziót az A-val szemközti hozzáírt körre, melynek középpontját F jelöli. Az ABC háromszög oldalai (mivel érintik e kört) mind azonos sugarú körökbe transzformálódnak. Feltehetjük, hogy ez a sugár egységnyi, és a megfelelő körök középpontjai OA,OB és OC. Az ABC körülírt körének a képe az A', B' és C' pontokon átmenő k1 kör lesz. (A vesszős változat az adott pont inverzió utáni képet jelöli.)
Azt állítjuk, hogy a k1 kör szintén egyégnyi sugarú. OA, OB és OC ugyanis egyaránt egységnyi távolságra vannak az F-től, így a rajtuk átmenő kör sugara is egységnyi. Az OAOBOC háromszög oldalfelezőpontjai által meghatározott háromszög körülírt körének sugara tehát 12. E háromszög csúcsai az FA', FB' és FC' szakaszok felezőpontjai, tehát az említett 12 sugarú kört egy F közepű 2-szeres nagyítás a k1-be viszi, mely így csakugyan egységsugarú.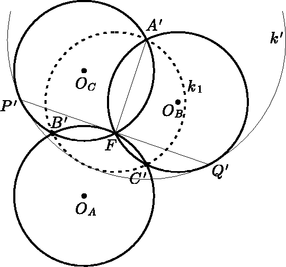
 
 

Az A' körüli 2 egység sugarú kör belülről érinti az AB, ill. AC oldalak képeit és a körülírt kör képét is, így e kör éppen k képe lesz az inverzió során. A P', Q' pontok pedig az A'-vel átellenes pontok a megfelelő egyégsugarú körökön, ezért A'FP' és A'FQ' egyaránt derékszögek, továbbá F (a szimmetria miatt) felezi P'Q'-t. Mivel F volt az inverzió középpontja, F egyúttal a PQ szakaszt is felezi.  □
 
Megjegyzések. 1. Hasonlóan a tavalyi verseny első feladatához, idén sem volt haszontalan a síkbeli inverzió tulajdonságainak ismerete (jóllehet tavaly többen próbálkoztak az alkalmazásával). A versenybizottság fenntartja magának az inverzióval (is) megoldható példa kitűzésének jogát.
2. A feladat szoros rokonságot mutat az 1978. évi Nemzetközi Matematikai Diákolimpián kitűzött 4. feladattal. A különbség lényegében annyi, hogy az olimpiai feladatban a k kör belülről érintett, és az érintési pontok alkotta szakasz felezőpontja a beírt kör középpontja volt. Az említett feladatra megjelent1 egyik szellemes megoldás ötlete könnyen alkalmazható a mi esetünkre is. Ezt vázoljuk az alábbiakban.
3. Több versenyző próbálkozott az analitikus módszerrel. Természetesen így is teljes értékű megoldás kapható, azonban viszonylag kevesen jártak sikerrel.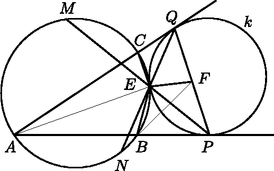
 
II. megoldás. Legyen E a k kör és az ABC háromszög körülírt körének érintési pontja, M, ill. N pedig a PE, ill. QE egyeneseknek és a háromszög körülírt körének E-től különböző metszéspontja. Mivel E-ből a k kört egy középpontos hasonlóság viszi az ABC háromszög körülírt körébe, az M-ben, ill. N-ben a körülírt körhöz húzott érintők párhuzamosak AB-vel, ill. AC-vel. Eszerint M felezi a C-t tartalmazó AB ívet, N pedig felezi a B-t tartalmazó AC ívet.
 
 

Felhasználva a kerületi szögek egyenlőségét, illetve hogy feleakkora ívhez feleakkora kerületi szög tartozik
MEB∢=MEA∢+AEB∢=β+α2+γ=π+γ2
adódik, ahonnan
BEP∢=π-MEB∢=α+β2.
(Felhasználtuk, hogy α+β+γ=π.)
Világos, hogy ABEC húrnégyszög, így a konkáv BEC∢ nagysága π+α. Legyen F az iménti szög felezőjének és a PQ szakasznak a metszéspontja. Eszerint
BEF∢=π+α2,ésAPF∢=π-α2,
hiszen az AQP háromszög egyenlő szárú. Azt kaptuk, hogy FEBP húrnégyszög, melyben a PF íven nyugvó kerületi szögre
PBF∢=PEF∢=BEF∢-BEP∢=π+α2-α+β2=π-β2.
Az adódott tehát, hogy BF az ABC háromszög B-nél lévő külső szögének a felezője.
A fenti számolás értelemszerű módosításával adódik, hogy CF az ABC háromszög C-nél levő külső szögfelezője. A két külső szögfelező F metszéspontja egyfelől a BC oldalhoz hozzáírt kör középpontja, másfelől rajta van az ABC háromszög A-ból induló szögfelezőjén. E szögfelező azonban felezi az egyenlő szárú APQ háromszög alapját, az állítást igazoltuk.  □
 
2. feladat. Határozzuk meg a legkisebb olyan, 2004-től különböző, pozitív egész n számot, amelyhez létezik olyan egész együtthatós f(x) polinom, hogy az f(x)=2004 egyenletnek legalább egy, az f(x)=n egyenletnek pedig legalább 2004 különböző egész megoldása van.
 
Megoldás. Legyen g(x) egy kívánt tulajdonságú polinom a feladatbeli n számhoz. Létezik tehát olyan a egész, melyre g(a)=2004. Definiáljuk a g1(x):=g(x+a) polinomot. Nyilván g1(0)=g(a)=2004, azaz g1(x) konstans tagja 2004, továbbá a g1(x)=n egyenletnek léteznek különböző, a1,a2,...,a2004 egész gyökei, melyek egyike sem 0, mivel g1(0)=2004. Ez azt jelenti, hogy
g1(x)-n=(x-a1)(x-a2)...(x-a2004)⋅g2(x),
ahol a polinomosztás miatt a g2(x) polinom is egész együtthatós, konstans tagja legyen c. Az egyenlőségben szereplő két polinom konstans tagjai megegyeznek, így persze
|2004-n|=|a1|⋅|a2|⋅...⋅|a2004|⋅|c|,
ahonnan, felhasználva, hogy c≠0, kapjuk, hogy
|2004-n|≥|a1|⋅|a2|⋅...⋅|a2004|≥|1|⋅|-1|⋅|2|⋅|-2|⋅...⋅|1002|⋅|-1002|.
Innen látszik, hogy 0<n<2004 nem lehetséges, ezért a fenti egyenlőtlenségből n≥(1002!)2+2004 következik.
Legyen most a g(x) polinom a következő:
g(x):=-(x-1)(x+1)(x-2)(x+2)...(x-1002)(x+1002)+(1002!)2+2004.
Erre a polinomra g(0)=2004 és
g(±k)=(1002!)2+2004
minden 1≤k≤1002 egészre, vagyis a feladat kérdésére a válasz
n=(1002!)2+2004.□

 
3. feladat. Egy körvonal mentén néhány kék és piros pontot helyeztünk el. Ezekkel az alábbi műveleteket végezhetjük:
(a) valahova beillesztünk egy új piros pontot, és a két szomszédját ellentétes színűre változtatjuk.
(b) ha legalább három pont van, és ezek közül legalább az egyik piros, akkor egy piros pontot törlünk, a két szomszédját pedig ellentétes színűre változtatjuk.
Kezdetben két pont van a kör kerületén, mindkettő kék. Elérhetjük-e a lépések többszöri alkalmazásával, hogy újra két pontunk legyen, de azok pirosak legyenek?
 

I. megoldás. A piros és kék pontok a kört ívekre osztják; írjunk minden egyes ívre (+1)-et vagy (-1)-et úgy, hogy a piros pontok két oldalán egyenlő, a kék pontok két oldalán pedig ellentett számok álljanak. Mivel a kék pontok száma minden lépésben párossal változik, ezért mindig páros sok kék pont van a körvonalon. Az ívek fenti számozása tehát kétféleképpen végezhető el, és az egyik számozásból úgy kapjuk a másikat, hogy minden íven előjelet váltunk. Megmutatjuk, hogy az ívekre írt számok összege minden lépés után osztható marad 3-mal. A kezdeti állapotban ez igaz, mert egy (+1)-et és egy (-1)-et adunk össze.
Ha egy lépésben egy i ívre piros pontot ültetünk, akkor a beillesztett piros pont szomszédjainak színe megváltozik, ezért a lépés előtti ívszámozásból helyes ívszámozást kapunk, ha a beillesztett piros pont két oldalán keletkező részívekre az i ívre írt szám ellentettjét írjuk, a további íveken pedig megtartjuk a számozást. Piros pont törlésekor fordítva járunk el. Az ívekre írt számok összege mindkét esetben 3-mal változik, tehát ha korábban 3-mal osztható volt az összeg, úgy ez a lépés után is így marad.
Ha néhány lépés után két piros pont marad, akkor két egyenlő szám kerül a kör kerületére, melyek összege nem osztható 3-mal. Ezt az állapotot tehát nem lehet elérni.  □
 
II. megoldás. Ismét azt igazoljuk, hogy nem kaphatunk két piros pontot az adott lépésekkel. Feleltessünk meg a pontoknak egy-egy geometriai transzformációt: a kék pontok jelentsék a t-vel jelölt tengelyes tükrözést az x-tengelyre, a piros pontok pedig az f-fel jelölt, origó körüli, 120∘-os elforgatásnak feleljenek meg.
Megmutatjuk, hogy azokban a pontrendszerekben, amelyek két kék pontból kiindulva előállíthatóak, a pontoknak megfeleltetett egybevágósági transzformációk szorzata ‐ tetszőleges kék vagy piros pontból indulva és pozitív körüljárás szerint haladva ‐ a minden pontot fixen hagyó, identikus transzformáció. Ez a kezdeti állapotban (két tükrözés) teljesül. Elegendő tehát megmutatnunk, hogy a lépések megőrzik ezt a tulajdonságot, hiszen két piros pontra a megfelelő egybevágóságok szorzata egy -120∘-os forgatás.
Először is figyeljük meg, hogy ha egy rögzített kék vagy piros p pontból kiindulva a megfelelő transzformációk szorzata minden pontot helyben hagy, akkor tetszőleges p' ponttól kezdve a transzformációk elvégzését, szintén az identikus transzformációt kapjuk. Ez azért igaz, mert ha p-től p'-ig (pozitív körüljárás szerint) a transzformációk szorzata egy τ egybevágóság, akkor a p'p íven a szorzat szükségképpen a τ-1 inverz leképezés. Ha viszont p'-ből indulunk, akkor a szorzat transzformációt úgy kapjuk, hogy először a τ-1, majd a τ transzformációt végezzük el, ám ez a leképezés-sorozat is minden pontot helyben hagy.
Tegyük tehát fel, hogy valamely állapotban a transzformációk szorzata az identitás, és tekintsünk egy tetszőleges lépést. A lépés négyféle lehet:
ff⇔tft,ft⇔tff,tf⇔fft,tt⇔fff;
a transzformációk szorzata egyik esetben sem változik, ha a kiindulópont a megváltozott pontokon kívülre esik, tehát legalább egy esetben. Láttuk, hogy a transzformációk szorzata ekkor bármely kiinduló pontból az identitás lesz, amivel állításunkat igazoltuk.  □
1ld. Reiman ‐ Dobos: Nemzetközi Matematikai Diákolimpiák 1959‐2003 (328‐332. oldal)