Kezdőlap


Cím:	Oktotó
Szerző(k):	Tusnády Gábor
Füzet:	1976/október, 52 - 57. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az alábbi feladatokat bárki megoldhatja foglalkozásra és életkorra való tekintet nélkül. Tulajdonképpen nem is kell a feladatokat megoldani a szó hagyományos értelmében, elég megtippelni az eredményt. A tippeket a mellé-kelt szelvényen vagy hozzá hasonló táblázatban lehet beküldeni. Határidő : 1976. november 20. Címünk KÖMAL/OKTOTÓ, 1443 Budapest, Postafiók 129.

A számtotó feladataira beküldött tippeket a következő képlet szerint értékeljük ki :

\begin{matrix} Q = \sum_{i = 1}^{8} S_{i} {(T_{i} - V_{i})}^{2}, \end{matrix}

ahol

T_{i}, V_{i}

i

-edik feladatra adott tipp, illetve végeredmény,

S_{i}

a feladat nehézségétől függő szorzószám (általában

S_{i} = 1

, ha azonban a feladat a vártnál nehezebbnek bizonyult,

S_{i} 0, 01

vagy akár

0, 0001

is lehet, és

Q

a tippek pontosságát mérő kvadratikus eltérés. A győztes ebben a versenyben az lesz, aki a legkisebb

Q

-t éri el. A betűtotó győztese pedig az, akinek a legtöbb találata van. Ez a két verseny egymástól is, a pontversenytől is független. A beküldött szelvényeket kiértékelve visszaküldjük mindazoknak, akik szelvényükhöz megcímzett és bélyeggel ellátott válaszborítékot mellékelnek.

Számtotó

1. Mennyi az

A, B, C, D

számok legnagyobbika, ha teljesül rájuk, hogy

\begin{matrix} A + 10 B + C = 10, B + 20 C + D = 20, C + 30 D + A = 30, D + 40 A + B = 40 ? \end{matrix}

2. Mennyi az

a_{0} = 1

a_{n + 1} = \frac{1}{3} (a_{n}^{3} + \sqrt[^{3}]{a_{n}})

n = 0, 1, 2, ...

feltételekkel meghatározott sorozat

100

-adik tagja ?

3. Két testvér egy

10 m

sugarú, kör alakú telken osztozik. Az egyik lekaszálja, a másik a telek szélén levert cövekhez kötött kecskéjével legelteti le a telken nőtt lucernát. Hány méteres legyen a kecske kötele, hogy igazságos legyen az osztozás ?

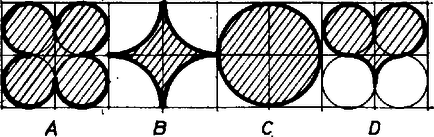
4. Írjunk egységnyi sugarú gömböket egy, két egység élű kocka csúcsai köré. Mekkora a sugara annak a gömbnek, amelyik még épp hogy elfér közöttük ?

5. Legyen

S

azoknak az

(x, y)

számpároknak a száma, amelyekben

x

is,

y

is egész, és

\begin{matrix} x^{2} + x y + y^{2} < 1000. \end{matrix}

Mennyi

S

ezredrésze ?

6. Mennyi a

0 < x \leq 2, 0 < y \leq 3

tartományban értelmezett

\begin{matrix} f (x, y) = x \frac{x^{2} + y^{2}}{x + y} \end{matrix}

függvény maximuma ?

7. A törökök megparancsolták, hogy Szolnok adóját a város bírója, papja, kántora, kovácsa és számadó juhásza közül választott küldöttség vigye Budára. Azt is előírták, hogy egy-egy küldöttségnek legalább két tagja legyen, és megtiltották, hogy különböző alkalmakon azonos összetételű küldöttség szerepeljen. Legfeljebb hányszor fizethettek adót a szolnokiak ?

8. Hány fokkal volt magasabb Budapesten a hőmérséklet napi középértéke 1976. július 15-én a százéves átlagnál ?

Betűtotó

1. Melyik az

A, B, C, D

számok legnagyobbika, ha teljesül rájuk, hogy

\begin{matrix} A + 10 B + C = 10, B + 20 C + D = 20, C + 30 D + A = 30, D + 40 A + B = 40 ? \end{matrix}

2. Tekintsük az

a_{0} = 1

b_{0} = \frac{1}{3},

\begin{matrix} a_{n + 1} = \frac{1}{3} (a_{n}^{3} + \sqrt[3]{a_{n}}); b_{n + 1} = \frac{1}{3} (b_{n}^{3} + \sqrt[3]{b_{n}}); (n = 0, 1, 2, ...) \end{matrix}

feltételekkel meghatározott sorozatokat, és legyen

Δ = | a_{100} - b_{100} |

. Melyik igaz az alábbi négy állítás közül ?

\begin{matrix} A) Δ \leq 0, 001; B) 0, 001 < Δ \leq 0, 01; C) 0, 01 < Δ \leq 0, 1; D) 0, 1 < Δ \end{matrix}

Beküldhető 1976. november 20-ig Címünk: KÖMAL/OKTOTÓ
1443 Budapest, Postafiók 129

1976.október SZÁMTOTÓ Sorszám:2/1

\begin{matrix} SZÁM & KÓD & TIPP \\ 1. & Legnagyobb gyök \\ 2. & Száz köbgyökvonás \\ 3. & Két testvér kecskéje a körben \\ 4. & Nyolc gömb közti gömb sugara \\ 5. & Rácspontok számának ezrede \\ 6. & (x^{3} + x y^{2}) / (x + y)maximuma \\ 7. & Szolnok adója \\ 8. & Hány fokkal volt melegebb ? \\ KVADRATIKUS ELTÉRÉS \end{matrix}

3. Az ábrán bemutatok néhányat anyám tésztaszaggatói közül. Melyiket használja anyám, ha kevés tésztát szeretne újragyúrni ?

4. Legyen

r

a számtotó 4. feladatának az eredménye. Melyik igaz az alábbi négy állítás közül ?

\begin{matrix} A) r \leq 0, 9; \end{matrix}

5. Hogy hívják a koordináta-rendszer

x^{2} + x y + y^{2} = 1000

egyenletű görbéjét ?

\begin{matrix} A) asztroid; \end{matrix}

Beküldhető 1976. november 20-ig. Címünk: KÖMAL/OKTOTÓ
1443 Budapest, Postafiók 129.

\begin{matrix} A BEKÜLDŐ ADATAI \\ Neve:..... \\ ..... \\ Címe:..... \\ ..... \\ Foglakozása:..... \\ ..... \\ Iskolája:..... \\ ..... \end{matrix}

1976. október Sorszám: 2/1

\begin{matrix} SZÁM & KÓD & TIPP \\ 1. & Melyik a legnagyobb ? \\ 2. & Perturbáció \\ 3. & Tésztaszaggatók \\ 4. & Kilencedik gömb \\ 5. & Hogy hívják ? \\ 6. & Algebrai számok \\ 7. & Melyik téves ? \\ 8. & Mi valószínűbb ? \\ A TALÁLATOK SZÁMA \end{matrix}

6. Melyik igaz az alábbi négy állítás közül ?
A) Vannak olyan

n, a_{0}, a_{1}, ...

, egészek, amelyekre

n > 0, a_{n} \neq 0

, és

\begin{matrix} a_{0} + a_{1} π + ... + a_{n} π^{n} = 0, \end{matrix}

ahol

π

a Ludolf-féle szám.
B) Vannak olyan

n, a_{0}, a_{1}, ..., a_{n}

egészek, amelyekre

0 < n < 100, a_{n} \neq 0

és

\begin{matrix} a_{0} + a_{1} x + ... + a_{n} x^{n} = 0, \end{matrix}

ahol

x = \sqrt[100]{1000.}

C) Van olyan

x

valós szám, melyhez tetszőleges pozitív

n

egész mellett található olyan véges

K

szám és végtelen

p_{i}, q_{i} (i = 0, 1, 2, ...)

sorozat, amelyekre

p_{i}, q_{i}

, egész, és

\begin{matrix} | x - \frac{p_{i}}{q_{i}} | < í \frac{K}{q_{i}^{n}} (i = 1, 2, ...) . \end{matrix}

D) Ha egy

x

valós számnak megvan a

C

-ben mondott tulajdonsága, akkor találhatók hozzá olyan

n, a_{0}, a_{1}, ..., a_{n}

egészek, melyekre

n > 0, a \neq 0

és

\begin{matrix} a_{0} + a_{x} + ... + a_{n} x^{n} = 0. \end{matrix}

7. Melyik téves az alábbi négy állítás közül ?
A) A hányados deriválásáról szóló szabály megtalálható G. W. Leibniz: Nova methodus pro maximis et minimis, itemque tangentibus, etc. című dolgozatában, mely az Acta Eruditorum című folyóiratban jelent meg 1684-ben, a 467-473. oldalakon.
B) A hányados deriválásáról szóló szabályt Londonban I. Newton már Leibniz előtt nyomtatásban közölte Philosophiae naturalis principia mathematica című művében.
C) A Cauchy-féle középértéktételt Cauchy 1829-ben közölte Lecons sur le calcul différentiel című munkájában.
D) Weierstrass analízisről szóló előadásaiban megmutatta, hogy van olyan mindenütt folytonos függvény, amely sehol sem deriválható.

8. Melyik a legvalószínűbb az alábbi négy esemény közül ?
A) Két érmét feldobva, mind a kettő fejre esik.
B) Tíz érmét feldobva, 5 esik fejre.
C) Száz érmét feldobva, 50 esik fejre.
D) Száz érmét feldobva, 100 esik fejre.

A májusi oktotó nyertesei

A számtotó nyertese: Zsigmond Géza (Budapest, Fazekas M. Gyak. Gimn.), kvadratikus eltérése

0, 0306

. Jó eredményt értek el a következők: Köteles Zoltán (Budapest;

0, 86)

, Major Zoltán (Budapest;

1, 24

), Peták Kálmán (Szolnok;

2, 0823

), Poronyi Gábor (Pécs;

4, 00

), Molnár Balázs (Budapest;

4, 02

), Gulyás Mihály (Orosháza;

6, 11

), Kovács Gábor (Pécsely;

8, 54

).
Ennél több, de

10^{2}

-nél kisebb a

Q

-ja 5 beküldőnek; ennél több, de

10^{4}

-nél kisebb 8-nak, ennél több, de

10^{6}

-nál kisebb 1-nek; ennél több 1-nek.
A betűtotó nyertese: Gubics József (Székesfehérvár, Ságvári E. Szakközépiskola), találatainak száma: 6. Szintén 6 találatot ért el Baksai Róbert (Győr), Gulyás Mihály (Orosháza), Homonnay Géza (Budapest), Major Zoltán (Budapest) és Peták Kálmán (Szolnok), közülük sorsolással választottuk ki a nyertest. Öt találatot heten, négyet hatan, hármat négyen, kettőt négyen, egyet ketten értek el, és egy találat sem volt egy szelvényen.

Megjegyzések a májusi oktotóhoz

Módosított Kürschák. Az eredeti rekurzió

a_{n + 1} = a_{n} + 1 / a_{n}

volt, és azt kellett belátni, hogy

a_{0} = 5

-ből indulva az ezredik tag

45

és

45, 1

között lesz. Ez a sorozat tart a végtelenbe, de a tagjai jól közelíthetők a

b_{n} = \sqrt[]{2 n + 25}

sorozat tagjaival. (Érdemes megvizsgálni, mihez tart az

n (a_{n} - b_{n})

sorozat.) Márciusban a rekurziót

(a_{n} + 1 / 2 a_{n})

-re módosítottam, ettől a sorozat konvergenssé vált, így a századik tagra már a 4-5-ödik tag jó közelítést adott. Egész más természetű a májusi

a_{n} - 1 / a_{n}

sorozat: ez se nem konvergál, se nem monoton, és nemhogy nem adható használható közelítés a tagjaira, de azok még számológépen sem számolhatók, ha csak a szokásos 8-10 értékes jeggyel dolgozunk. Ezért aztán a tippek között volt mindenféle:

182;