Cím: SZÁMÍTÁSTECHNIKAI ROVAT
(Rovatvezető: Ada-Winter Péter)
Szerző(k):  Ada-Winter Péter 
Füzet: 1978/október, 72 - 75. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az aranymetszés

 

Számrendszerünk, méréseink alapja az egyenlő részekre való osztás, például a kettes számrendszerben a felezés. Így kapunk egyre kisebb részeket, amelyekkel aztán tetszőleges adatot közelíthetünk. A kettes számrendszerben minden számjegy helyi értéke az előtte állóénak fele, és kétszer akkora, mint a mögötte állóé. Vizsgáljuk meg, mi történik, ha olyan helyi értékekkel dolgozunk, amelyek közül két szomszédos összege egy harmadikkal egyenlő. Például ‐ az egységnyi helyi érték bal szomszédját A-val, jobb szomszédját a-val jelölve ‐ ezekre és az 1-re teljesüljön
A=1+a.(1)
Mivel azt most is meg szeretnénk tartani, hogy a szomszédos helyi értékek aránya állandó legyen, ez azt jelenti, hogy
a:1=1:(1+a).(2)
Ez nyilván legfeljebb csak egy pozitív a számra teljesülhet, hiszen ha egy a-ra teljesül, akkor minden 0<x<a számra a (2) jobb oldala nagyobb, mint a bal oldala:
11+x>11+a=a>x,
és x>a mellett sem állhat fenn egyenlőség:
11+x<11+a=a<x.
Ez az ún. aranymetszés egyenlete, mellyel már a régi görögök is foglalkoztak a szabályos tízszög szerkesztésével kapcsolatban.
 
 

Mint ismeretes, ha C1,C2,C3 az egységnyi sugarú, O középpontú körbe írt szabályos tízszög csúcsai, és C2C3 egyenese az OC1 sugár meghosszabbítását M-ben metszi, akkor MC1=C1C2, és a C3MO háromszög hasonló a C2OC3 háromszöghöz. Emiatt a C1C2=a számra épp a (2) egyenlet teljesül. Ha a C1C3 szakasz hosszát p-vel jelöljük, a C3 pontnak a C1 középpontú, M-en át-menő körre vonatkozó hatványa alapján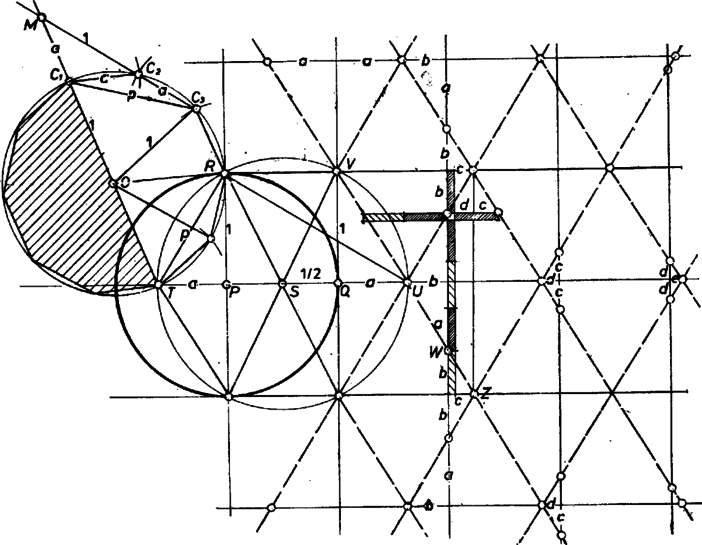
p2-a2=a(1+a),
ami viszont (2) alapján 1-gyel egyenlő. Ennek alapján ha PQ, PR a P középpontú, egységnyi sugarú kör egymásra merőleges sugarai, és PQ felezőpontja S, akkor az S körüli, R-en átmenő kör PQ-nak P-n túli meghosszabbítását abban a T pontban metszi, amelyre TP=a,TR=p. Valóban, ha ez a kör PQ-nak Q-n túli meghosszabbítását U-ban metszi, akkor a TPR,RPU háromszögek hasonlósága alapján azt kapjuk, hogy a TP=QU=a távolságra is teljesül (2), és a TPR háromszögben 1+a2=p2.
 
 

Legyen V a PQR háromszöget négyzetté kiegészítő pont, és rajzoljuk meg a síkon azt a négyzetrácsot, amelynek ez az alapnégyzete. Vizsgáljuk meg, hogyan helyezkedik el ebben a négyzetrácsban az UV egyenes. Jelöljük az U-n túli meghosszabbításán keletkező első két metszéspontot W-vel és Z-vel, (1-a)-tb-vel. Könnyen látható, hogy W is a,b részekre osztja a négyzetrács őt tartalmazó oldalát, és ha a Z-nél keletkező kisebbik szakaszt c-vel jelöljük,
c:b=b:a.
Ha tehát (b-c)-t d-vel jelöljük, azt kapjuk, hogy a c és d szakaszok ugyanolyan arányban osztják a b szakaszt, mint a és b az egységszakaszt. Emiatt
c=a-b,d=b-c.
Hasonlóan tovább menve egy végtelen sorozatot kapunk, amelynek minden eleme az előző két elem különbsége. A másik irányban pedig az
A=1+a,B=1+A,C=A+B
tagokkal kezdve olyan sorozatot kapunk, amelynek minden tagja a megelőző kettő összege. Ha az UV egyenest tükrözzük a PQ,RV egyenesekre, és a kapott alakzatot lépésről lépésre tükrözzük ezekre az egyenesekre, egy végtelen hálózatot kapunk, amelynek a szemei a p oldalú rombuszok. Nevezzük aranymetszés származékoknak azokat a szakaszokat, amelyeket ennek a hálózatnak az elemei az eredeti négyzetrácsból kimetszenek.
 

Feladatok
 

A megoldásokat a következő címre lehet beküldeni: dr. Ada-Winter Péter, Munkaügyi Minisztérium Számítástechnikai Intézet, Budapest, Reguly A. u. 57‐59. 1089. Határidő: 1978. november 10. A feladatok megoldását november 22-én beszéljük meg a szakkörön.
 
1. Mutassuk meg, hogy 2a=2b+c+d+e,2=5b+e. (Lásd az ábra kereszt alakú részét.)
 
2. Mutassuk meg, hogy b=a2,c=a3, és általában az 1,a,b,c,... sorozat tagjai a hatványai. Hasonlóan A hatványai az 1,A,B,C,... sorozat tagjai.
 
3. Mutassuk meg, hogy az aranymetszés származékok előállíthatók a véges sok (tetszőleges előjelű egész kitevőjű) hatványának összegeként.
 
4. Mutassuk meg, hogy két aranymetszés származék szorzata előállítható a véges sok (tetszőleges előjelű egész kitevőjű) hatványának összegeként.
 
5. Nevezzük arany-egészeknek mindazokat a valós számokat, amelyek előállíthatók a véges sok (tetszőleges előjelű egész kitevőjű) hatványának összegeként. Alakítsunk ki szubrutin-családot az arany-egészek közti műveletek elvégzésére. Legyen K és N általunk választott, a gépi konfigurációnak megfelelő természetes szám. Azokat az arany-egészeket fogjuk megengedettnek tekinteni, amelyek felírhatóak ∑i=-NNciai alakban, ahol |ci|≤K egész szám. Minden egyes arany-egésznek feleltessünk meg egy (2N+1) méretű tömböt, ebben tartsuk a c-N,...,c-1,c0,c1,...,cN együtthatókat.
a) Az IDENT nevű szubrutin két arany-egészről döntse el, hogy egyenlőek-e.
b) Az ADD nevű szubrutin adjon össze két arany-egészet. (Ha az eredmény nem megengedett szám, adjon hibajelzést, és állítsa le a futást.)
c) A MULT nevű szubrutin szorozzon össze két arany-egészet. (Hasonlóan adjon hibajelzést, ha kell.)
d) Mondjuk azt, hogy egy arany-egész kanonikus alakú, ha benne |ci|≤1, és a 0-tól különböző együtthatók előjele egyenlő. Írjunk szubrutint, amely tetszőleges arany-egészet kanonikus alakra hoz.
e) Írjunk szubrutint, amely tetszőleges valós számhoz megkeresi a hozzá legközelebb levő megengedett arany-egészet.
 

*
Az 1978. évi 5. számban kitűzőtt feladatok és megoldásaik
 

1. Állítsa elő a harmadik, negyedik és ötödik gyököket közelítő sorozat Newton-Raphson képleteit.
 

Megoldás.

xi+1=13(2xi+axi2);xi+1=14(3xi+axi3);xi+1=15(4xi+axi4).

2. Készítsen szubrutint, amely Newton-Raphson eljárással négyzetgyök közelítő értéket számít. Az NR2 azonosítójú szubrutin átveszi az A-val jelölt alapot, a Q-val jelölt kezdőértéket és a hibakorlátot.
 

Megoldás. A MASTER PR15 csekély átalakításával (amelyet nem közlünk) az alábbi szubrutin is hívható:
 


   SUBROUTINE NR2(A,Q,EPS,B,N)   WRITE (3,3)   N=0   X1=Q  2   IF(ABS(X1**2-A)-EPS)1,1,0   X2=(X1+A/X1)/2.   N=N+1   IF(ABS(X1-X2)-EPS)1,1,0   X1=X2   GO TO 2  1   B=X2   RETURN  3   FORMAT(///10X,23HNEWTON-RAPHSON MÓDSZER:)   END  
 

3. Melyek a Newton-Raphson eljárás alkalmazhatóságának szükséges feltételei ?
 

Megoldás. Miután eddig tárgyalt példáink csak egyszerű hatványfüggvényekre szorítkoztak, a kérdés is csak ilyen függvényekre értendő. Ilyen esetekben, mivel a folytonosság, deriválhatóság és egyéb lényeges tulajdonságok adottak, elég kikötnünk, hogy a közelítés intervallumában az első derivált ne váljon sehol sem zérussá.