Kezdőlap


Cím:	Számítástechnikai rovat (11)
Szerző(k):	Ada-Winter Péter
Füzet:	1977/december, 212 - 215. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az előző részben kitűzött feladat megoldása
Feladat:

Program készítendő, amely a példaként hozott egyenletrendszer együtthatóit kártyáról beolvassa, és az egyenletet eliminációs módszerrel megoldja. A program álljon két szubrutinból, az első az eliminációt, a második a visszahelyettesítést hajtsa végre. Nyomtatandók egymás alatti sorokban az adott egyenletrendszer egyenletei és néhány sorral ezek alatt az eredményül kapott gyökök. Az egyenletek együtthatói három kártyán helyezkednek el, egy kártyán 15‐15 karakterszélességű mezőben három tizedesjegy pontossággal egy egyenlet együtthatói.

1. ábra

Megoldás:

A program, melynek blokkdiagramját az 1. ábrán látjuk, az alábbi lehet:

\begin{matrix} MASTER  PR12 \\ DIMENSION  A(3,4),X(3) \\ READ(1,100)((A(I,J),J=1,4),I=1,3) \\ WRITE(3,101)((A(I,J),J=1,4),I=1,3) \\ CALL  ELIM(A) \\ CALL  VISSZ  (A,X) \\ WRITE(3,102)((K,X(K)),K=1,3) \\ 100 & FORMAT  (2(4F15.3/), 4F15.3) \\ 101 & FORMAT  (1H1,5(/),30X,22HAZ EREDETI EGYUTHATOO. \\ X & 8H  MATRIX:///3(30X,4(F15.3,5X)//)) \\ 102 & FORMAT (////30X, 11HA GYOEKOEK://3(30X, 1HX, |1, \\ Y & 3H =,F15.5//)) \\ STOP \\ END \\ SUBROUTINE  ELIM(EH) \\ DIMENSION  EH(3,4) \\ DO  2  |=2,3 \\ B=EH(|,  1)/EH(1.1) \\ DO  1  J=1,4 \\ 1 & EH(|, J)=B*EH(1,J)-EH(|,J) \\ 2 & CONTINUE \\ B=EH(3,2) /EH(2,2) \\ DO  3  J=2,4 \\ 3 & EH(3, J)=B*EH(2,J)-EH(3,J) \\ RETURN \\ END \\ SUBROUTINE VISSZ (EH,V) \\ DIMENSION EH(3,4), V(3) \\ DO  2  K=1,3 \\ J=4-K \\ IF (J-2)3,4,0 \\ C=O \\ GO  TO  5 \\ 4 & C=V(J+1)*EH(J,J+1) \\ GO  TO  5 \\ 3 & C=V(J+2)*EH(J,J+2)+V(J+1)*EH(J,J+1) \\ 5 & V(J)=(EH(J,4)-C)/EH(J,J) \\ 2 & CONTINUE \\ RETURN \\ END \\ FINISH \end{matrix}

Megjegyzés:
Bizonyára sokan vannak, akik az eliminációs részben az alábbi (vagy elvileg azzal megegyező) ciklust szervezték:

\begin{matrix} DO  2  |=2,3 \\ DO  1  J=1,4 \\ 1 & EH(|,J)=(EH(|,1)*EH(1,J)/EH(1,1)-EH(|,J) \\ 2 & CONTINUE \end{matrix}

Ez hibás, mert ameddig J=1, addig EH(I,1) értékes

2

, de ha I=2, akkor EH(I, 1) értéke zérus és az is marad a negyedik ciklusig! Vagyis az első menetben a második egyenletnek csak az első együtthatója lenne helyes, a többi már nem.

6.1 fejezet folytatása

Tekintsünk most egy általánosan felírt elsőfokú

n

ismeretlenes egyenletrendszert:

\begin{matrix} a_{1, 1} \cdot x_{1} + a_{1, 2} \cdot x_{2} + ... + a_{1, n} \cdot x_{n} = a_{1, n + 1} \\ a_{2, 1} \cdot x_{1} + a_{2, 2} \cdot x_{2} + ... + a_{2, n} \cdot x_{n} = a_{2, n + 1} \\ ⋮ \\ a_{n, 1} \cdot x_{1} + a_{n, 2} \cdot x_{2} + ... + a_{n, n} \cdot x_{n} = a_{n, n + 1} \end{matrix}

aminek rövidebb írásmódja:

\begin{matrix} \sum_{j = 1}^{n} a_{i, j} x_{j} = a_{i, n + 1} (i = 1, 2, 3, ..., n) \end{matrix}

(Ezek felelnek meg a korábban

E_{0, i}

-val jelölt egyenleteknek.) A program az egyenletrendszerből csak az együtthatókat és az abszolút tagokat veszi át, mint adatokat, és ezekből számítja a gyököket.

Az együtthatók

n

soros, és

n + 1

oszlopos mátrixot alkotnak:

\begin{matrix} (\begin{matrix} a_{1, 1} & a_{1, 2} & ... & a_{1, n} & a_{1, n + 1} \\ a_{2, 1} & a_{2, 2} & ... & a_{2, n} & a_{2, n + 1} \\ ⋮ \\ a_{n, 1} & a_{n, 2} & ... & a_{n, n} & a_{n, n + 1} \end{matrix}) = {[a_{i, j}]}_{n, n + 1} \end{matrix}

Az a megszorítás, hogy csak inhomogén egyenletekkel foglalkozunk, azt jelenti, hogy a mátrix

(n + 1)

-dik oszlopában nem lehet valamennyi elem zérus, azaz

\begin{matrix} \sum_{i = 1}^{n} | a_{i, n + 1} | \neq 0 \end{matrix}

Ezen kívül, mivel bizonyos együtthatókkal osztanunk kell, ideiglenesen feltételezzük, hogy az osztó együtthatók nem zérusok. Később ennek tisztázására visszatérünk. Az első menetből kapott egyenletek az alábbiak:

\begin{matrix} E_{1, 1} & = E_{0, 1} & \to & \sum_{j = 1}^{n} a_{1, j} \cdot x_{j} = a_{1, n + 1} \\ E_{1, 2} & = \frac{a_{2, 1}}{a_{1, 1}} \cdot E_{0, 1} - E_{0, 2} & \to & \sum_{j = 1}^{n} (\frac{a_{2,1}}{a_{1, 1}} \cdot a_{1, j} - a_{2, j}) x_{j} = \frac{a_{2, 1}}{a_{1, 1}} \cdot a_{1, n + 1} - a_{2, n + 1} \\ E_{1, 3} & = \frac{a_{3, 1}}{a_{1, 1}} \cdot E_{0, 1} - E_{0, 3} & \to & \sum_{j = 1}^{n} (\frac{a_{3, 1}}{a_{1, 1}} \cdot a_{1, j} - a_{3, j}) x_{j} = \frac{a_{3, 1}}{a_{1, 1}} \cdot a_{1, n + 1} - a_{3, n + 1} \\ E_{1, n} & = \frac{a_{n, 1}}{a_{1, 1}} \cdot E_{0, 1} - E_{0, n} & \to & \sum_{j = 1}^{n} (\frac{a_{n, 1}}{a_{1, 1}} \cdot a_{1, j} - a_{n, j}) x_{j} = \frac{a_{n, 1}}{a_{1, 1}} \cdot a_{1, n + 1} - a_{n, n + 1} . \end{matrix}

A menet során az eredeti együttható mátrixot változtatjuk meg, mivel ha minden menetben újabb mátrixot akarnánk betölteni, igen nagy tárkapacitást kellene lekötnünk, fölöslegesen.

Az új együttható mátrixot is

{[a_{i, j}]}_{n, (n + l)}

-el jelöljük és azt mondjuk, hogy az első menet során a mátrix elemeinek aktuális értéke megváltozott. Ennek eredményeként az első oszlopban a második sortól lefelé minden elem zérus.

Az eddig elmondottakat egy példán mutatjuk be:

Legyen az egyenletrendszer

10

ismeretlenes, jelöljük az együttható mátrixot

A

-val. Az első menetet a 2. ábrán látható blokkdiagram alapján készített program valósítja meg.

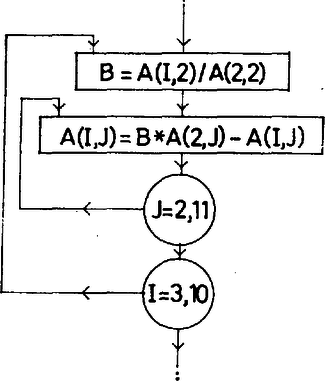2. ábra

Visszatérve az általános tárgyalásmódra vizsgáljuk meg a második menetet.

\begin{matrix} E_{2, 1} = E_{1, 1} \to változatlan \\ E_{2, 2} = E_{1, 2} \to változatlan \\ E_{2, 3} \to & \sum_{j = 1}^{n} (\frac{a_{2, 3}}{a_{2, 2}} \cdot a_{2, j} - a_{3, j}) x_{j} = \frac{a_{2, 3}}{a_{2, 2}} \cdot a_{2, n + 1} - a_{3, n + 1} \\ E_{2, 4} \to & \sum_{j = 1}^{n} (\frac{a_{2, 4}}{a_{2, 2}} \cdot a_{2, j} - a_{4, j}) x_{j} = \frac{a_{2, 4}}{a_{2, 2}} \cdot a_{2, n + 1} - a_{4, n + 1} \\ ⋮ \\ E_{2, n} \to & \sum_{j = 1}^{n} (\frac{a_{2, n}}{a_{2, 2}} \cdot a_{2, j} - a_{n, j}) x_{j} = \frac{a_{2, n}}{a_{2, 2}} \cdot a_{2, n + 1} - a_{n, n + 1} \end{matrix}

Az együttható mátrix aktuális értékei ezzel újra megváltoztak, mégpedig úgy, hogy a második oszlop elemei a harmadik sortól kezdve szintén zérus értékűek lettek. Példánkra vonatkozóan a 3. ábra mutatja a második menetnek megfelelő blokkdiagramot.

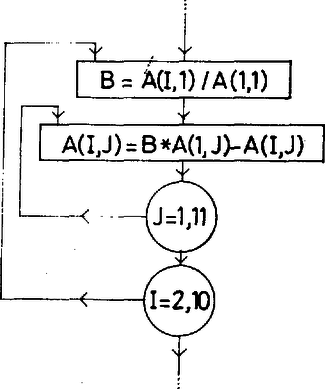3. ábra

Az elmondottakból következik, hogy általános esetben

(n - 1)

, példánk esetében 9 menet lehetséges az elimináció során.

Feladat:

1) Blokkdiagram készítendő a 10 ismeretlenes lineáris egyenletrendszer eliminációs program részletéhez.

2) Az elkészült blokkdiagram alapján ELIM azonosítójú SUBROUTINE készítendő.