Cím: Az Iskolarádió matematikai szakköre
Szerző(k):  Herczeg János 
Füzet: 1977/november, 154 - 155. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Felhívjuk a figyelmet, hogy december 5-i programunk megváltozott! Pólya György professzor ősszel pár napra Magyarországra látogatott abból az alkalomból, hogy a Magyar Tudományos Akadémia tiszteletbeli tagjává választotta. A gondolkodás iskolája, A problémamegoldás iskolája írója ezúttal is hajlandó volt találkozni a középiskolásokkal is. A Budai Nagy Antal Gimnáziumban, több iskola tanulóiból álló hallgatóságnak bemutatott valamit abból, hogyan szokott ő tanítani.
Következő szakkörünkön ebből az előadásból hallunk részleteket. Címnek ezt választottuk:

 
Be van-e bizonyítva?

 
Az előadásban ugyanis az úgynevezett izoperimetrikus problémával kapcsolatos néhány vizsgálatot láthattunk, és a kérdés mindig az volt, eljutottunk-e a megoldás bizonyításához? Az izoperimetrikus probléma azok közé a kérdések közé tartozik, amelyekre a válasz szemléletes alapon kézenfekvő, a bizonyítás azonban korántsem könnyű. Arról van szó, hogy az egyenlő kerületű síkidomok közül melyiknek van a legnagyobb területe? Azonnal érezzük, hogy a megoldás a kör, de mikor tekinthetjük ezt az állítást bizonyítottnak?
Mivel a szakkörön ismertetett meggondolások geometriai jellegűek, jó ha megismerkedünk az ott bemutatott legfontosabb ábrákkal:
 

 

1. ábra. Ez azt illusztrálja, hogy konkáv síkidom nem lehet a probléma megoldása, mert tudunk konstruálni vele egyenlő kerületű, de nála nagyobb területű konvex síkidomot.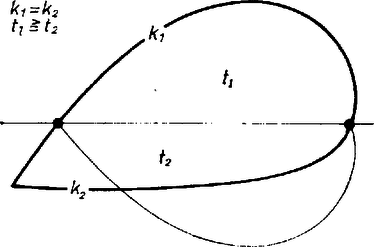
 

 

2. ábra. Elég olyan síkidomok között keresni a megoldást, amelyeknek van szimmetriatengelyük. Vágjuk ugyanis ketté a síkidomot egy kerületfelező húrral. A két rész közül a nem kisebb területűt tükrözzük a húr egyenesére.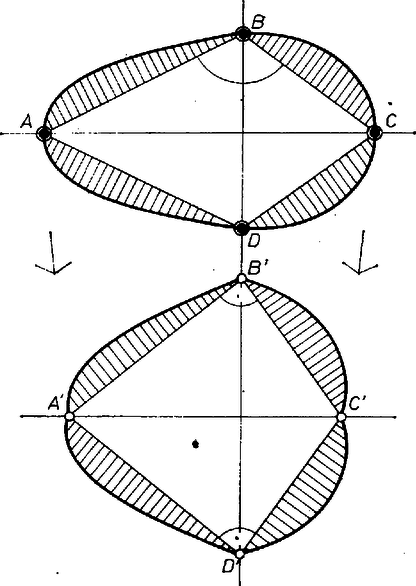
 

 

3. ábra. Ha a konvex síkidomnak van szimmetriatengelye (AC), akkor ha kerületének van olyan B pontja, amelyből ez nem látszik derékszög alatt, a kerületének hosszát megtartva, növelhetjük a területét a következő módszerrel: az ABCD deltoidhoz legyenek ,,hozzáragasztva'' azok a szeletek, amelyeket oldalai az eredeti síkidomból levágtak. A deltoid viszont legyen csuklósan mozgatható, és a B-be és D-be futó oldalakat állítsuk be merőlegesekre. (A'B'=AB, B'C'=BC, de A'B'C∢ derékszög.)
A többit hallgassuk meg a Rádióban december 5-én, a 3. Műsorban, 15.30-16.00-ig.
Az izoperimetrikus problémáról olvashatunk a következő könyvekben: Számokról és alakzatokról (Tankönyvkiadó, Szakköri Füzet), Courant-Robbins: Mi a matematika (Gondolat).