Cím: Számítástechnikai Rovat
Szerző(k):  Ada-Winter Péter 
Füzet: 1977/november, 149 - 153. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az előző részben kitűzött feladatok megoldása

 
Feladatok: 1. Az alábbi feladatok legfeljebb 10×10-es méretű, egész típusú számokat tartalmazó tömbre vonatkoznak.
a) Szubrutin készítendő, amely m soros, n oszlopos mátrixban (2≤m≤10, és 2≤n≤10) fölcseréli az i-edik sor elemeit a j-edik sor elemeivel ahol i≠j, 1≤i≤m és 1≤j≤n. A szubrutin átveszi a mátrixot, az i és j számokat és az átvett mátrixot módosítva adja vissza. (Az eredeti szövegben n és m jelentése fel volt cserélve.)
b) A fentihez hasonló megkötéssel szubrutin készítendő oszlopcserére.
c) Program készítendő, amely felcseréli a legnagyobb sorösszegű sort a legkisebbel, valamint a legnagyobb oszlopösszegű oszlopot, a legkisebbel. Nyomtatandó az eredeti mátrix, a cserélt sorú és (az eredetihez mérten) cserélt oszlopú mátrix.
A 2. feladat megoldását nem közöljük.
 
Megoldás: Az alábbiakban bemutatjuk a program főszegmensét, a sorösszegét számító (ROE), a legnagyobb és legkisebb elemen kereső (NAKI), és a sorcserélő (SORCS) szubrutinokat. Nem közöljük az oszlopösszeget számító (POE) az oszlopot cserélő (OSZCS) és a tömböt kiíró (MAWR2) szubrutinokat.
Az 1.a) és 1.b) ábrán a ROE és NAKI szubrutinok blokkdiagramjai láthatók.
 

 

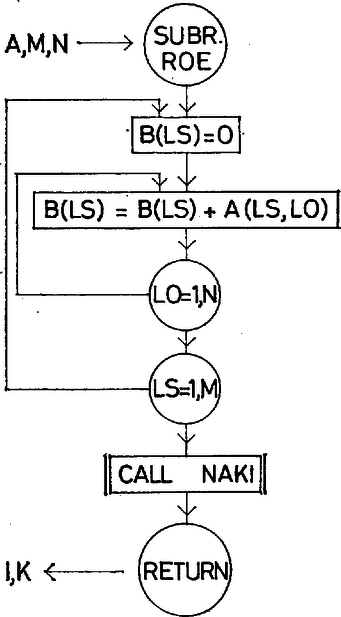1a. ábra
 

 

 

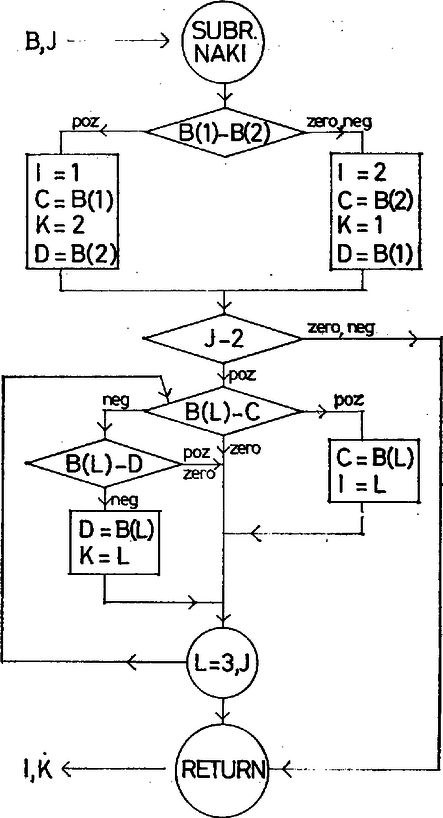1b. ábra
 

MASTER PR11INTEGER A(10,10)DO 2 I=1,10  2READ(1,3)(A(1J)J=1,10)READ(1,1)M,NCALL MAWR2(A,M,N)CALL ROE(A,M,N,IS,KS)CALL SORCS(A,M,N,IS,KS)CALL MAWR2(A,M,N)CALL SORCS(A,M,N,IS,KS)CALL POE(A,M,N,IO,KO)CALL OSZCS(A,M,N,IO,KO)CALL MAWR2(A,M,N)  1FORMAT(2(2X,12))  3FORMAT(1018)STOPEND  6SUBROUTINE ROE(A,M,N,I,K)  2INTEGER A(M,N),B(10)DO 1 LS=1,MB(LS)=0DO 2 LO=1,N  2B(LS)=B(LS)+A(LS,LO)  1CONTINUECALL NAKI(B,M,I,K)RETURNENDSUBROUTINE NAKI(B,J,I,K)INTEGER B(J),C,DIF(B(1)-B(2))3,0,0I=1C=B(1)K=2D=B(2)GO TO 4  3I=2C=B(2)K=1D=B(1)  4IF(J-2)10,10,0DO 5 L=3,JIF(B(L)-C)6,5,0C=B(L)I=LGO TO 5  6IF(B(L)-D)0,5,5D=B(L)K=L  5CONTINUE  10RETURNENDSUBROUTINE SORCS(A,M,N,I,K)INTEGER A(M,N),B(10)DO 7 L=1,NB(L)=A(I,L)A(I,L)=A(K,L)  7A(K,L)=B(L)RETURNEND

SUBROUTINE OSZCS(A,M,N,I,K)...ENDSUBROUTINE POE(A,M,N,I,K)...ENDSUBROUITNE MAWR2(A,M,N)...ENDFINISH

 
Megjegyzések:
- A főszegmensben először a 10×10-es tömböt olvassuk be, majd az m és n indexeket, melyekről feltesszük, hogy az előírt korlátokon belül vannak. Az m×n-es részmátrix a 10×10-es mátrixban a bal felső sarok felé tömörítve helyezkedik el.
- A főszegmensben a cserélt sorú mátrix nyomtatása után újra cseréltetjük a sorokat, hogy visszaálljon az eredeti mátrix.
- Figyeljük meg az A tömb átadását a ROE és a SORCS szubrutinokban. A-val együtt M és N indexeket is átadjuk és a szubrutinokban levő deklarációkban egész változók állnak az indexek helyén. Ilyenkor dinamikus indexhatárról beszélünk, ami lényegében az átadott tömb méretének változtathatóságát jelenti adott korlátokon belül. Ez csakis SUBROUTINE és FUNCTION szegmensekben fordulhat elő és csakis úgy,
- ha a szubrutin nyitó utasításának zárójelpárja közt szerepel a tömbazonosító és az indexéül használt (egy vagy több) egész változó;
- ha a dinamikus indexeknek adott számértékek nem nagyobbak a hívószegmensben deklarált tömb számértékű indexeinél.
 
6. Elsőfokú, többismeretlenes (inhomogén) egyenletrendszer megoldására szolgáló program
 
6.1. Az eliminációs módszer
 
Elsőfokú, többismeretlenes egyenletrendszer gyökeinek meghatározására számos, a számítástechnikában is alkalmazható módszert ismerünk. Pl.: a közismert Cramer-szabályon alapuló megoldás is programozható, de számítógépidő-felhasználás szempontjából gazdaságtalan. A gyakorlatilag hasznosítható eljárások felsorolásával, ismertetésével nem foglalkozhatunk. Az alábbiakban egy közismert, esetenként jól használható számítógépes eljárást mutatunk be, mely az un. Gauss-féle eliminációs módszeren alapul. Az eljárást egy numerikus példán tesszük érthetővé. Az egyenleteket Em,n-nel fogjuk jelölni. Az egyenletrendszert ún. ,,menetek''-ben alakítjuk át, a kiindulási egyenletre m=0, az első menet után kapott egyenletrendszerre m=1 stb. Egy adott meneten belül az egyenleteket az n indexszel sorszámozzuk. Pl.: E3,5 jelenti a harmadik menet után kapott egyenletrendszerben az ötödik egyenletet. Numerikus példánk, a megjelölt egyenletekkel az alábbi:
E0,1:3x1+4x2+3x3=1,E0,2:2x1-x2-x3=6,E0,3:x1+3x2+2x3=-1.
Az egyes menetekben az átalakításokat is jelölni fogjuk.
Ha k konstans, akkor k⋅Ei,j az egyenlet mindkét oldalán álló kifejezésnek k-val való szorzását, Ei,j+Ek,1 a két egyenlet megegyező oldalain álló kifejezéseinek összegezését jelenti stb. Az első menet után kapott egyenletek:
E1,1=E0,1:3x1+4x2+3x3=1,E1,2=23⋅E0,1-E0,2:113x2+3x3=-163,E1,3=13⋅E0,1-E0,3:-53x2-x3=43.

Példánk második, egyben utolsó menete:
E2,1=E1,1:3x1+4x2+3x3=1,E2,2=E1,2:113x2+3x3=-163,E2,3=-53⋅311E1,2-E1,3:-411x3=3633.

Az eljárás eddigi szakaszában (két menetben) a három ismeretlenből kiküszöböltünk (elimináltunk) kettőt. Ez az eljárásnak ún. eliminációs része. Az eljárás következő szakaszában az egyenletekben alulról felfelé végighaladva kifejezzük az ismeretleneket: E2,3-ból x3-at, E2,2-ből x2-t, E2,1-ből x1-et. Ez az ún. visszahelyettesítő rész. Eredményül az x1=2, x2=1 és x3=-3 gyököket kapjuk. Már az eddigiekből is nyilvánvaló, hogy a menetek száma az egyenletek számánál eggyel kevesebb.
 

Feladat:
Program készítendő, amely a példaként hozott egyenletrendszer együtthatóit kártyáról beolvassa, és az egyenletet eliminációs módszerrel megoldja. A program álljon két szubrutinból, az első az eliminációt, a második a visszahelyettesítést hajtsa végre. Nyomtatandók egymás alatti sorokban az adott egyenletrendszer egyenletei és néhány sorral ezek alatt az eredményül kapott gyökök. Az egyenletek együtthatói három kártyán helyezkednek el, egy kártyán 15-15 karakterszélességű mezőkben három tizedesjegy pontossággal egy egyenlet együtthatói.