Kezdőlap


Cím:	Az Iskolarádió Matematika Szakköre
Füzet:	1977/február, 75 - 77. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A legkisebb négyzetek módszere

Lapunk 53. kötetének 175. oldalán egy fizikafeladat megoldása során egy tömegpont pályájáról kiderül, hogy egyenlete

\begin{matrix} s (t) = A t^{2} + B t + C + D sin (ω t + δ) \end{matrix}

alakú, és a konstansok értéke

\begin{matrix} A = \frac{1}{2}, B = \frac{2}{π}, C = 0, D = \frac{2}{π^{2}}, ω = π δ = 0. \end{matrix}

Gyakran találkozunk ehhez hasonló feladattal: ismerjük egy függvényt definiáló képlet alakját, bizonyos hibával megmérjük néhány helyen a függvény értékét, és ezek alapján meg szeretnénk határozni a képletben szereplő ismeretlen együtthatók értékét. Nyilván olyan együtthatókat fogunk választani, amelyek a legjobb közelítést adják. De mit jelent az, hogy legjobb közelítés ?
A fizikusok mérési adataihoz mi is kitűztünk egy feladatot (F. 2037.). Elhagytuk a szinuszos tagot, és azt a parabolát kerestük, amelytől vett maximális eltérés a legkisebb. Mint kiderült így a feladatot elég nehéz megoldani. A megoldás alapötletét újra kitűztük a 2063-as ^{$^{*}$} feladatban, ennek alapján megtalálható az általános módszer is, a végrehajtása azonban igen nagy munka.
Ezek a nehézségek vezethették Gausst arra az elhatározásra, hogy csillagászati számításaiban ne az abszolút hibával mérje a közelítés jóságát, hanem a kvadratikus eltéréssel. Általában, ha az

x_{i}

y_{i}

, (

i = 1, 2, ..., n

) mérési adatokat az

y = f (x)

függvénnyel közelítjük, a kvadratikus eltérés a

\begin{matrix} Q = {(y_{1} - f (x_{1}))}^{2} + {(y_{2} - f (x_{2}))}^{2} + ... + {(y_{n} - f (x_{n}))}^{2} \end{matrix}

összeg. Ezt kényelmesebb felírni a szumma jel segítségével:

\begin{matrix} Q = \sum_{i - 1}^{n} {(y_{i} - f (x_{i}))}^{2} . \end{matrix}

A Gausstól származó legkisebb négyzetek módszere alapján valahányszor sok függvény közül kell választanunk, mindig azt részesítjük előnyben, amelyikhez a legkisebb kvadratikus eltérés tartozik.
Ha a figyelembe vett függvények

f (x) = a x + b

alakúak, feladatunk annak az

a

b

számpárnak meghatározása, amelyre a

\begin{matrix} Q = \sum_{i - 1}^{n} {(y_{i} - a x_{i} - b)}^{2} \end{matrix}

négyzetösszeg minimális. Ezt az

a

b

számpárt kell meghatározni, vagy a megfelelő egyenest megrajzolni a mellékelt 3. feladatban közölt adatokhoz. (Sorozatunkban összesen hat feladatot tűzünk ki. Az első kettő az adásban szerepelt.)

3. feladat Melyik egyenes alapján lehet a legjobb becslést adni a gyerek magasságára ?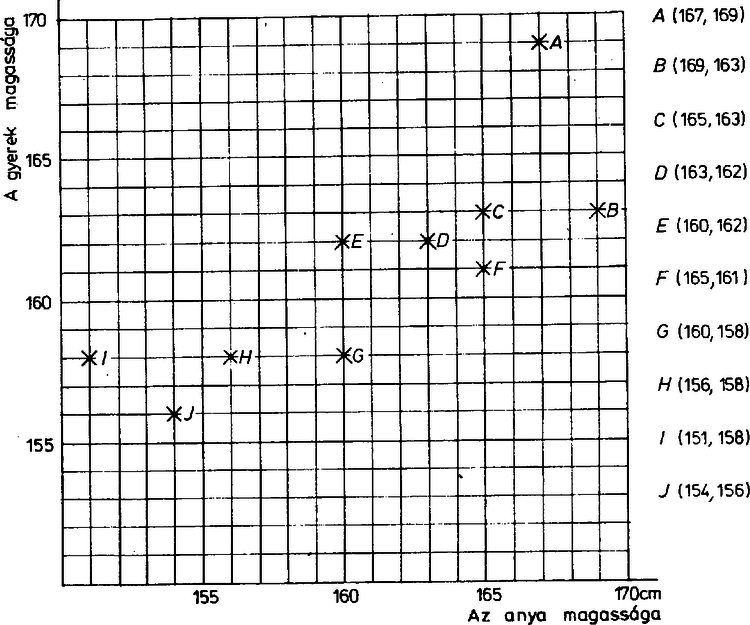

4. feladat. Ha

9

kockát feldobunk, amelyek mindegyikének

k

lapja piros, akkor

100

esetből várhatóan hányszor fordul elő, hogy a piros lapok közül legfeljebb

n

van felül ?

\begin{matrix} n, k & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ 0 \\ 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \\ 7 \\ 8 \\ 9 \end{matrix}

Fogadjunk !

Varga Tamástól származik a következő játék (a szabályait kissé módosítottuk). Választunk egy véletlen eseményt, amelyet akárhányszor meg tudunk ismételni, lényegében hasonló körülmények között. Jelöljük ezt az eseményt

E

-vel. Mondjuk

E

az az esemény, hogy ha

9

kockát feldobunk, melyek mindegyikének

1

lapja piros, akkor a piros lapok közül legfeljebb

3

van felül. A játékosok mindegyike felírja egy lapra, hogy szerinte a választott esemény

100

esetből várhatóan hányszor fordul elő. (Amíg ezzel mindenki el nem készül, a játékosok ne nézzék meg, mit írtak a többiek.) A tippek alapján kiosztjuk a szerepeket. Aki a legnagyobb számot írta, az lesz a Felső, tippjét jelöljük

F

-fel. Aki a legkisebb számot írta, az lesz az Alsó, tippje

A

. (Egyenlőség esetén Felső is, Alsó is több játékos is lehet egyszerre.) A többiek a kibicek. Ezután levonunk a Felsőtől

F

, Alsótól (

100 - A

) pontot, és minden kibicnek adunk (

F - A

) pontot. Végül a Felső megkísérli az

E

eseményt előidézni. Egyetlen kísérletet végezhet, ha ebben

E

bekövetkezik, ő kap

100

pontot, különben Alsó. Ha tehát

E

a mondott esemény, akkor a Felső feldob

9

kockát, és megszámolja, hogy hány piros lap kerül felülre. Ha ezek száma legfeljebb

3

, a Felső, különben pedig Alsó kap

100

pontot.
Ezt a játékot a kedves olvasó is játszhatja családja vagy barátai körében, a mellékelt 4. feladatban szereplő hetven esemény bármelyikével. Célszerű sorról sorra haladni, de akit a két szélső oszlop zavar, az hagyja ki őket. Mi sajnos nem tudunk mindenkivel játszani, így arra kérjük az olvasót, higgye el nekünk, hogy tudjuk a pontos eredményt (és azt is, hogy ez mit jelent). Mi a hozzánk beérkező tippeknek a pontos értékről vett kvadratikus eltérését fogjuk kiszámolni, és játékunkat az nyeri, akinek a legkisebb a kvadratikus eltérése.

Öröklődés

Ketten játszhatják a következő játékot. Választanak egy nem túl nagy számot jelöljük ezt

n

-nel, mondjuk

n = 3

, és megállapodnak abban, hogy a magyar kártya számozott lapjai annyi pontot érnek, amennyi a rajtuk levő szám, az alsó, felső, király ász, pontértéke pedig rendre

11

12

13

14

. Mindkét játékos kap

2 n

darab lapot, és felír egy cédulára egy számot. (Se a lapjait, se a számát nem mutatja meg a másiknak.) Aztán mindketten kihúznak

n

lapot, a másik lapjai közül, és összeadják az együtt kihúzott

2 n

lap pontértékét. Az nyer, akinek a céduláján levő szám közelebb van a kapott összeghez. (Kár volna tagadni, hogy ez a játék Czeizel doktor tévébeni előadásainak a hatására jutott eszünkbe).

^{$^{*}$} A két feladat megoldását márciusi számunkban közöljük. (A Szerk.)