| Cím: | Számítástechnikai rovat | ||
| Szerző(k): | Ada-Winter Péter | ||
| Füzet: | 1977/március, 115 - 121. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 5. Mindenekelőtt a korábbi közleményeinkben előfordult hibákat igazítjuk helyre. ‐ Az 1976. évi 6. szám 21. oldalán szó esik a programlapon az utasításmezőben elhelyezhető karakterek számáról. Erre nézve a helyes korlát. ‐ Az 1976. évi 7. szám 76. oldalán szerepel egy nyomtatási utasítás negyedik variánsa. Ez helyesen az alábbi: A januári számban kitűzött feladataink megoldásai 1. Készítsünk programot négyzet alapú csonka gúlák térfogatának kiszámítására, ha az egyik négyzet területe minden számításnál egységnyi, a másiké között változik. lépésközzel. Az alábbi nyolc magassággal kell a térfogatot számítani: . Az oszlopok felett nyomtassuk ki az -betűt és közvetlen mellette az indexeket. A térfogatokat négy tizedesjeggyel nyomtassuk. A program utasításfüggvény felhasználásával készüljön. Megoldás Programunkban utasításfüggvény számítja a csonka gúla képletét VOL azonosítóval deklaráltuk, két formális paramétere a csonkagúla magassága és az egyik négyzet oldala. A ciklusban egy TERF azonosítójú mátrixot töltünk fel úgy, hogy minden oszlopban más értékadó utasítással számítjuk a térfogatot. Figyeljük meg, hogy itt a VOL aktuális paraméterei esetenként kifejezések, azokon belül standard függvények is szerepelhetnek. A ciklus befejeztével egy azonosítójú egydimenziós tömb (vektor) betöltése következik, amely az M mellé nyomtatandó indexeket tartalmazza. Ezeket az első WRITE utasítással írjuk a mátrix ,,fejlécébe''. Az alábbiakban bemutatjuk a programot. 2. Készítsünk programot a kétismeretlenes egyenletrendszer megoldására. A megoldásban alkalmazzunk másodrendű determinánsokat, s ezeket utasításfüggvényben számíttassuk ki. Az egyenletrendszert kell megoldani, ha A program nyomtassa ki az egyenletrendszereket és tőlük jobbra két tizedesjegy pontossággal a megoldásokat, ha azok léteznek, Ha nincs pontosan egy megoldás, akkor a VÉGTELEN SOK MEGOLDÁS, ill. a NINCS MEGOLDÁS szöveg nyomtatandó, aszerint, hogy melyik eset áll fenn. Megoldás A determinánsok: A megoldást az és összefüggések adják meg. Az egyenletrendszernek mindig van pontosan egy megoldása, ha . (A koordináta‐rendszerben a két egyenlet két egymást egy pontban metsző egyenes képét határozza meg.) Ha viszont , akkor , azaz . Az egyik egyenlet ismeretlenjeinek együtthatóit egy valós számmal való szorzás útján állíthatjuk elő a másik egyenlet megfelelő együtthatóiból, azaz és . Az egyenletrendszer megoldása szempontjából most két eset lehetséges. a) és . Ekkor nyilván , amiből látjuk, hogy az egyik egyenlet a másiknak következménye, az egyenletrendszert végtelen sok számpár elégíti ki. (A két egyenletnek megfelelő egyenes a koordináta-rendszerben egybeesik, minden pontjuk közös.) b) , de . Ilyenkor az egyenletrendszert ellentmondásosnak mondjuk, nincs olyan számpár, amely kielégítené. (Az egyenleteknek a koordináta‐rendszerben párhuzamos egyenesek felelnek meg.) Belátható, hogy ilyenkor és . Ha egyikük is zérus lenne, akkor . lenne, ami kiinduló feltételünknek ellentmond. Programunkban tehát először megvizsgáljuk -t, ha ez nem zérus, úgy képezzük a megoldást, ha zérus, akkor újabb vizsgálatot tartunk. Ha és közül csak egyik is zérus, akkor végtelen sok megoldás van, ha viszont egyik sem zérus, akkor egy megoldás sincsen. A programban a determinánsokat egy DET azonosítójú utasításfüggvény számítja, amelynek négy formális paramétere rendre a determináns első és második sorának elemei. Az egyenletrendszer hat paraméterének mindenkori (aktuális) értékeit a azonosítók tartalmazzák. A zérusra történő vizsgálat tulajdonképp azt nézi, hogy a szám beleesik-e egy zérus körüli zárt intervallumba. Erre azért kényszerülünk, mert a valós típusú számok ‐ a gépen belüli kerekítési, folyamatok miatt ‐ akkor sem lesznek pontosan zérus értékűek, amikor a számítás szerint azoknak kellene lenniük. Ezért bizonyos korlátnál és az alatt minden számított pozitív valós számot zérusnak tekintünk. Feladatunkban a rendszerdetermináns abszolút értékét zérusnak tekintjük, ha az -nél nem nagyobb. Ugyanis az ismeretlenek együtthatói egy tizedesjegy pontossággal vannak megadva, a rendszerdeterminánsok legfeljebb két nem zérus értékű tizedesjegyet tartalmazhatnak, a harmadik tizedesjegy zérus értékű kell, hogy legyen. Ezután következik a másik két determináns, és , melyek közül elegendő lenne egyiket vizsgálni, ha számolhatnánk annak pontos zérus értékével. Mivel nem így van, mindkettőt vizsgáljuk, éspedig a szorzatukat. Ha , akkor a determinánsokat zérusnak tekintjük. A ciklus menetében egyenletrendszer paramétereit az stb. tízelemű egydimenziós tömbökbe helyezzük, az eredményeket az ugyanilyen és tömbökbe. Az tömb jelzőszámokat tartalmaz. Egy adott egyenletrendszer esetében , ha az egy megoldás, , ha végtelen sok megoldása van, , ha az egyenletrendszernek nincs megoldása. 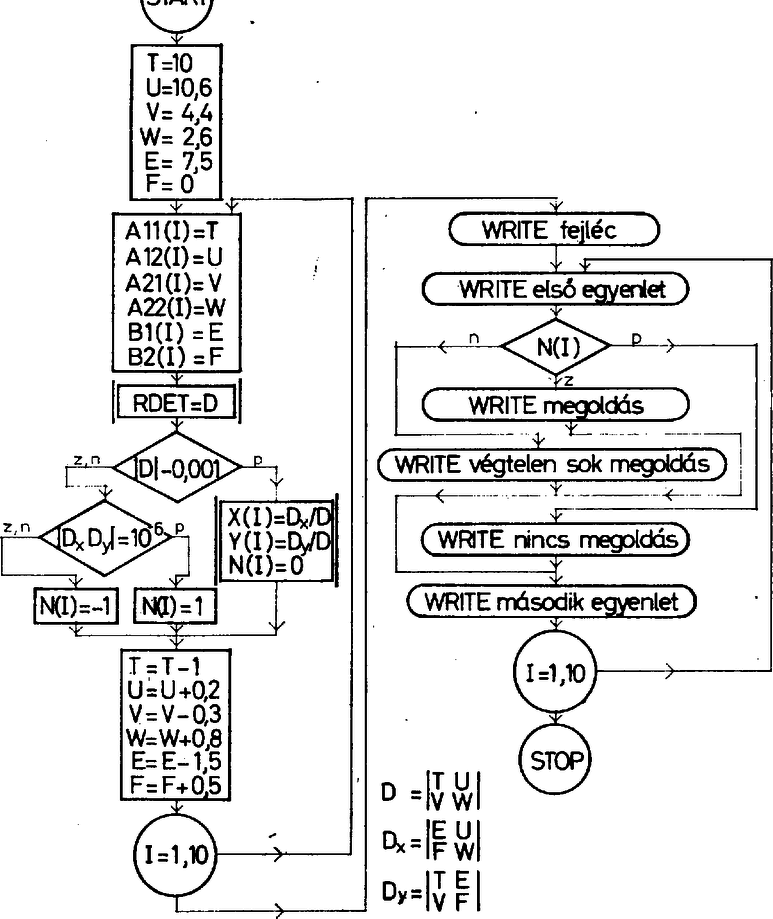 A papír bal felére az egyenletrendszereket, tőlük jobbra, a két egyenletrendszer közötti sorral egy vonalban, a megoldásokat nyomtatjuk. A két oszlop fölé feliratot íratunk ki. Az ábra a program blokkdiagramját mutatja. Ebben a kettős vonalú blokkok szubrutinhasználatra utalnak. (A rövid írásmód céljából a blokkban használtuk a és jeleket.) A program egy lehetséges formája az alábbi: 4.2 A FUNCTION szubrutin Van olyan feladat, melyben a szubrutin nem írható meg egy utasítással. Ilyenkor célszerű lehet a FUNCTION használata. Ennek a szubrutinnak is van mindig azonosítója, mely után zárójelben állnak a formális, illetőleg aktuális paraméterek. Ezekből legalább egy mindig kell, hogy szerepeljen és lehet közöttük tömbazonosító is. A FUNCTION végrehajtása során, annak azonosítója a szubrutinon belül legalább egyszer értéket kell, hogy kapjon és ezt az egy számot adja vissza az őt hívó programnak. A FUNCTION-on belül használt cimkék, azonosítók, tömbök függetlenek a hívó programrészbeliektől. A szubrutinból kiugrani GOTO vagy IF utasítások segítségével nem lehet. A RETURN utasítás visz vissza a hívó programba. Ebből legalább egy van egy szubrutinban. Ha a szubrutinban a program elágazik és a végrehajtás több ágon lehetséges, akkor egy‐egy ág végére helyezhetjük a RETURN utasítást. Emiatt ezt az utasítást a szubrutin logikai végének is nevezzük. A FUNCTION szubrutint egy END utasítás zárja le, amit a szubrutin fizikai végének nevezünk. Példaként tekintsük a következő függvényt: A szubrutin programja így írható: Mint látjuk, ezt a fajta szubrutint speciális utasítással nyitjuk meg, hasonlóan a MASTER szóval kezdődő programrészhez. Szabály, hogy a szubrutin első utasításában álló FUNCTION után szóköz, majd az általunk adott azonosító áll és ezt követik zárójelek közt a formális paraméterek. Ennek a szubrutinnak nem kell a hívó programban deklaráció. Hogy példánk teljes legyen, bemutatjuk azt a programot, amely ezt a szubrutint hívja. A program értékeit, mint egy sorozat elemeit képezi. Első elem és a további elemek képzési szabálya az alábbi összefüggés . A sorozat -nál nagyobb elemeit ne képezzük. Egymás melletti oszlopokba nyomtatandók a sorozat elemei és a velük képzett helyettesítési értékek. A program egy lehetséges formája a következő: A programlapra sorrendben első helyre mindig a MASTER-rel kezdődő programrész kerül. Ennek END utasítása után tetszőleges sorrendben közvetlenül következnek azok a szubrutinok, amelyek külön programrészként írandók. A hívóprogram példánkban tartalmazza a VEGYES (A) szubrutin behívását a harmadik sorban. Itt a zárójelben most aktuális paraméter áll, mivel a programban előtte az A már kapott értéket. A MASTER-rel kezdődő programrész után következő FUNCTION VEGYES (X) utasításban az X formális paraméter. A szubrutinon belül a VEGYES azonosító többször is értéket kap, de minden egyes értékadást követően egy RETURN utasítás hatására tér vissza a végrehajtás a hívó programrészbe. A szubrutin által számított számértéket PNYO nevű programunk harmadik sorában a B azonosító veszi fel. Lényeges tudnivaló, hogy a FUNCTION szubrutin tömbazonosítót is átvehet. Ezt látjuk az alábbi vázlatos programban. A MASTER-ban deklarált egydimenziós A tömböt és kétdimenziós B tömböt veszi át a DETERM nevű szubrutin. A tömbök elemei a kipontozott részben kapnak értéket. Vegyük észre, hogy az átadott tömböket a szubrutinon belül újra kell deklarálni. Feladatok 1. Készítsünk FUNCTION szubrutint, amely tetszőlegesen megadott koordinátájú két pont közötti távolság értékét számítja ki. 2. Készítsünk egy olyan FUNCTION szubrutint, amely legfeljebb 30 számadat átlagát számítja ki. (Az adatokat egy 30 elemű tömb, az adatok számát egy egész típusú azonosító tartalmazza.) 3. Készítsünk programot, melyben adott öt különböző pont koordinátáival. Számítsuk ki a fenti két szubrutin segítségével az összes lehetséges távolságot és ezek átlagát. Nyomtassuk ki feliratozva az adott öt pont koordinátáit, ugyancsak feliratozva a pontok közötti lehetséges távolságokat, végül újabb felirat mellett a távolságok átlagát. |