Kezdőlap


Cím:	Az 1972. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):	Surányi János
Füzet:	1973/február, 49 - 57. oldal	PDF \| MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Jelentse $a$ , $b$ , $c$ egy háromszög oldalainak a hosszát. Bizonyítsuk be, hogy fennáll a következő egyenlőtlenség:

\begin{matrix} a {(b - c)}^{2} + b {(c - a)}^{2} + c {(a - b)}^{2} + 4 a b c > a^{3} + b^{3} + c^{3} . \end{matrix}

I. megoldás. A bal oldal harmadik és negyedik tagja így alakítható át:

\begin{matrix} c {(a - b)}^{2} + 4 a b c = c {(a + b)}^{2} . \end{matrix}

Vonjuk le ezután a bal oldal egyes tagjaiból a jobb oldal megfelelő tagját, így a különbség szorzattá alakítható:

\begin{matrix} a (({b - c)}^{2} - a^{2}) + b ({(c - a)}^{2} - b^{2}) + c ({(a + b)}^{2} - c^{2}) = \\ = a (b - c - a) (b - c + a) + b (c - a - b) (c - a + b) + c (a + b - c) (a + b + c) = \\ = (a + b - c) (a b - a c - a^{2} - b c + a b - b^{2} + a c + b c + c^{2}) = \\ = (a + b - c) (- {(a - b)}^{2} + c^{2}) = (a + b - c) (a - b + c) (- a + b + c) . \end{matrix}

Itt mind a három tényező pozitív, mivel egy háromszög két oldalának az összege nagyobb a harmadiknál. Ezzel a feladat állítását igazoltuk.

Megjegyzések. 1. A feladat állítása így is fogalmazható: az egyenlőtlenség teljesülése szükséges feltétele annak, hogy

a

b

c

hosszúságú szakaszokból háromszöget lehessen szerkeszteni.
Könnyen látható, hogy pozitív

a

b

c

számokra szorítkozva a feltétel elégséges is. Valóban, ha az egyenlőtlenség teljesül, akkor az átalakítással nyert szorzat pozitív, tehát vagy mind a három tényező pozitív, vagy kettő negatív, egy pozitív. Az első esetben létezik

a

b

c

oldalú háromszög. Ha viszont pl. az első két tényező negatív volna, akkor az összegük,

2 a

is, holott

a

pozitív. Ez tehát nem lehetséges.
2. Ha a háromszög egy szakaszt lefedő két szakasszá fajul el, akkor a két oldal egyenlővé válik.

II. megoldás. A két oldal különbsége tagokra bontás után így alakítható át:

\begin{matrix} a (b^{2} + c^{2} - a^{2}) + b (c^{2} + a^{2} - b^{2}) + c (a^{2} + b^{2} - c^{2}) - 2 a b c . \end{matrix}

(1)

Ez, a háromszög

a

b

c

-vel szemközti szögeit, mint szokás,

α

β

γ

-val jelölve, a cosinustétel alapján így alakítható tovább:

\begin{matrix} 2 a b c (cos α + cos β + cos γ - 1) . \end{matrix}

Itt, felhasználva, hogy

α + β + γ = 180^{\circ}

, továbbá a könnyen igazolható

\begin{matrix} cos φ + cos ψ = 2 cos \frac{φ + ψ}{2} cos \frac{φ - ψ}{2}, \\ cos φ - cos ψ = 2 sin \frac{ψ - φ}{2} sin \frac{ψ + φ}{2}, \\ cos φ = 1 - 2 sin^{2} \frac{φ}{2} \end{matrix}

összefüggéseket^{$^{*}$}

\begin{matrix} cos α + cos β + cos γ = 2 cos \frac{α + β}{2} cos \frac{α - β}{2} + 1 - 2 sin^{2} \frac{γ}{2} = \\ = 2 cos (90^{\circ} - \frac{γ}{2}) cos \frac{α - β}{2} - 2 sin^{2} \frac{γ}{2} + 1 = \\ = 2 sin \frac{γ}{2} (cos \frac{α - β}{2} - sin (90^{\circ} - \frac{α + β}{2})) + 1 = \\ = 1 + 2 sin \frac{γ}{2} (cos \frac{α - β}{2} - cos \frac{α + β}{2}) = \\ = 1 + 4 sin \frac{γ}{2} sin \frac{β}{2} sin \frac{α}{2} . \end{matrix}

Ez a kifejezés nagyobb, mint

1

, mert

α / 2

β / 2

γ / 2

hegyes szögek, s így sinusaik pozitívok. Ezzel a feladat állítását igazoltuk.

Megjegyzés. Ha

(1)

-ben

- 2 a b c

helyett

- 3 a b c

-t írunk, a kifejezés már nem lesz pozitív. Ez volt az 1964. évi VI. Nemzetközi Matematikai Diákolimpia

2

. feladata.^{$^{*}$} Az állítás tetszés szerinti pozitív

a

b

c

számokra helyes marad, sőt míndkét oldalhoz

2 (a^{3} + b^{3} + c^{3})

-t adva a szimmetrikusabb

\begin{matrix} (a^{2} + b^{2} + c^{2}) (a + b + c) \leq 2 (a^{3} + b^{3} + c^{3}) + 3 a b c \end{matrix}

alak általánosítható a következő módon: Ha

a_{1}, a_{2} ..., a_{n}

nem-negatív számok, akkor

\begin{matrix} (a_{1}^{n - 1} + a_{2}^{n - 1} + ... + a_{n}^{n - 1}) (a_{1} + a_{2} + ... + a_{n}) \leq \\ \leq (n - 1) (a_{1}^{n} + a_{2}^{n} + ... + a_{n}^{n}) + n a_{1} a_{2} ... a_{n} . \end{matrix}

Ez viszont az 1968. évi Schweitzer Miklós matematikai emlékverseny (egyetemi hallgatók versenye)

2

. feladata volt.^{$^{*}$}

Második feladat. Egy osztályban ugyanannyi fiú van, mint lány (legalább

4

tanuló). Sorba állítjuk őket és megnézzük, ketté lehet-e vágni a sort úgy, hogy a kapott részekben is ugyanannyi fiú legyen, mint lány.
Jelöljük

a

-val az összes olyan sorrendeknek a számát, amelyekben ilyen kettévágás nem lehetséges és

b

-vel azokét, amelyekben létezik ilyen kettévágás, de csak egy.
Bizonyítsuk be, hogy

b = 2 a

.
Elegendő a sorrendeknél csak arra tekintettel lenni, hol állnak lányok, hol fiúk, hiszen ha már ki vannak jelölve a ,,lányhelyek'' és a ,,fiúhelyek'', akkor mindig ugyanannyiféleképpen tudjuk elrendezni a lányokat a lányhelyeken, és a lányok elhelyezésétől függetlenül ugyanannyiféleképpen a fiúkat a fiúhelyeken. A megoldásokban ezért csak a fiú‐lány sorrendek számával foglalkozunk.
Nevezzük azokat a sorrendeket, amelyek nem vághatók a feladatokban leírt módon ketté,

A

-típusúnak, azokat, amelyeknek egy ilyen kettévágásuk van,

B

-típusúnak.

I. megoldás. Jelöljük az első helyen álló tanulót és a vele egyező neműeket

X

-szel, a másik nemű tanulókat

Y

-nal. Ha

n

lány és

n

fiú van az osztályban, akkor eszerint

n

darab

X

-nek és

n

darab

Y

-nak az

X

-szel kezdődő sorrendjeit kell vizsgálnunk. Minden ilyen sorrendhez a fiúknak és lányoknak két sorrendje tartozik, az egyik, amelyikben

X

-et fiúnak és

Y

-t lánynak értelmezzük, és a másik a fordított értelmezéssel keletkező.
Egy

X

-szel kezdődő

A

-típusú elrendezésben bármely betűig ‐ az utolsó kivételével ‐ legalább eggyel több

X

fordul elő, mint

Y

, hiszen a két betű előfordulásszáma közti különbség betűről betűre haladva eggyel változik, tehát ha

X

-szel kezdődik a sor, akkor az

Y

-ok csak úgy kerülhetnének túlsúlyba, ha előzőleg egyenlővé vált volna az

X

-ek és

Y

-ok száma. Ez azonban

A

-típusú elrendezésben csak az utolsó betűnél következhet be.
Egy

B

-típusú elrendezés a kettévágásnál két

A

-típusúra bomlik szét. Ezek közül az első

X

-szel kezdődik, a második azonban kezdődhet

X

-szel is,

Y

-nal is. Azok, amelyekben a második rész is

X

-szel kezdődik, a

B

-típusú elrendezések felét teszik ki, mert ezek második részében felcserélve az

X

-eket és

Y

-okat, minden sorrendet megkapunk és mindegyiket csak egyszer. A feladat állítását tehát bebizonyítjuk, ha az

X

-szel kezdődő

A

-típusú elrendezéseket egyértelműen összepárosítjuk az olyan

B

-típusúakkal, amelyeknek mindkét

A

-típusú része

X

-szel kezdődik.
Egy kívánt hozzárendelés történhet úgy, hogy a

B

-típusú elrendezés második

A

-típusú részének élén álló

X

-et a sor legelejére állítjuk.
Ezáltal

A

-típusú elrendezést kapunk, ugyanis a

B

-típusú elrendezés első

A

-típusú részében, mint láttuk, egy tetszőleges betűig, az utolsó kívételével, legalább eggyel több

X

van, mint

Y

. Az egész elé téve egy

X

-et, a második betűtől kezdve tehát legalább

2

-vel több

X

lesz mint

Y

, egészen amíg az első

A

-típusú rész utolsó betűjéig nem érünk. Ez a betű a második

A

-típusú rész első betűje helyére került. Idáig eggyel több az

X

-ek száma, mint az

Y

-oké. A további betűket ugyanazok a betűk előzik meg, amelyek a

B

-típusú elrendezésben megelőzték, így megint több

X

lesz, mint

Y

, egészen az utolsó betűig.
A meggondolásból azt is látjuk, hogy fordítva egy

A

-típusú sorrendben a második olyan betűt kell megkeresni, ameddig eggyel több

X

szerepel,^{$^{*}$} mint

Y

, és ez után helyezni a sor elejéről az első

X

-et. Ezáltal

X

-szel kezdődő sorrendet kapunk, mert ha az

A

-típusú elrendezésben az első

X

-et egy

Y

követné, akkor mindjárt az után ketté lehetne vágni a sorrendet, hiszen legalább négy betűből áll a sor. Az első

X

elvételével az

X

-ek és

Y

-ok számának a különbsége

1

-gyel csökken, amíg el nem érjük az áthelyezett betű új helyét. Mivel az előtt

1

volt ez a különbség, most

0

-ra csökken, mégpedig itt először. Itt tehát kettévágható a sorrend, előbb azonban nem. Tovább megint az

X

-ek lesznek túlsúlyban, mig a sor végére nem érünk, hiszen az

X

új helyén túl minden betűig ugyanazok a betűk vannak a módosított sorrendben is, mint az eredetiben.
Ezzel a kívánt párosítást elvégeztük, s így a feladat állítását igazoltuk.

Megjegyzések. 1. Jelöljük a

k

fiú és

k

lány

A

-, ill.

B

-típusú sorrendjeinek számát

a_{k}

-val

(k \geq 1)

, ill.

b_{k}

-val

(k \geq 2)

. Egy

B

-típusú elrendezést csak páros számú betű után lehet kettévágni. Az olyan elrendezések száma, amelyben ez a

2 k

-adik betű után történik

(k = 1,2, ..., n - 1) (a_{k} / 2) \cdot a_{n - k}

, mert egy

2 k

betűből álló,

X

-szel kezdődő

A

-típusú elrendezést követ egy tetszés szerinti,

2 n - 2 k

betűből álló. Így

\begin{matrix} \frac{b_{n}}{2} = \frac{a_{1}}{2} \cdot a_{n - 1} + \frac{a_{2}}{2} \cdot a_{n - 2} + ... + \frac{a_{n - 1}}{2} \cdot a_{1} . \end{matrix}

A feladatot tehát megoldjuk, ha megmutatjuk, hogy

a_{n}

is felírható a jobb oldal formájában, vagy

2

-vel osztva és

a_{k} / 2

-t

a'_{k}

-vel jelölve

\begin{matrix} a'_{n} = a'_{1} \cdot a'_{n - 1} + a'_{2} \cdot a'_{n - 2} + ... + a'_{n - 1} \cdot a'_{1} . \end{matrix}

(1)

2. Tuza Zsolt, dolgozatában a következő probléma közvetítésével látja be

(1)

fennállását:
,,Hányféleképpen lehet egy kör (v. bármely konvex zárt vonal) mentén elhelyezett

2 k

pontot úgy összepárosítani, hogy a párokat összekötő húroknak ne legyen közös pontja?''
Megmutatja egyfelől, hogy a megfelelő összekötések száma

a'_{k + 1}

. Az összekötő húrok kisebb indexű végpontjához

X

-et, a nagyobb indexűhöz

Y

-t ír, majd sorra leírja az egymás utáni pontok mellé írt betűket és az elejére ír még egy

X

-et, a végére egy

Y

-t. Másfelől az első pontból induló átló két zárt vonalat képez a körből. Az egyikre és a másikra eső pontok külön‐külön egymást nem metsző húrokkal vannak összekötve. (Megegyezünk abban, hogy

0

pont összekötéseinek számán

a'_{1} = 1

-et értünk.) Ez a gondolat elvezet az

(1)

összefüggés igazolásához. A részletek végiggondolását az olvasóra bízzuk.
3. A fenti megszámlálási gondolat megfogalmazható az

A

-típusú elrendezések kettébontásaként az összekötési probléma közbeiktatása nélkül, ugyanis az első pontból induló húr végpontjának az a betű felel meg, amelynél másodszor csökken az addig előforduló

X

-ek és

Y

-ok számának különbsége

1

-re. Így az

A

-típusú elrendezéseknek a fenti megoldásban szereplő átalakításához jutunk, csak ezt most nem a

B

-típusú elrendezésekhez való hozzárendelésre használjuk, hanem összeszámláljuk segítségével az

A

-típusú elrendezéseket is ugyanúgy, mint föntebb a

B

-típusúakat. A részletek végiggondolását ismét az olvasóra bízzuk.
Ez a meggondolás azt mutatja, hogy az összekötési probléma szellemes közbeiktatása nélkülözhető, és tulajdonképpen a fenti megoldás egy variánsával állunk szemben.
4. Az

(1)

formula és az

a'_{1} = 1

kezdő érték módot ad az

a'_{n}

, s így egyben az

a_{n}

, értékek egymás utáni kiszámítására, az

a'_{n}

, értékek úgynevezett rekurzív meghatározására. Többen egy másik rekurzív meghatározást találtak:
Az összes,

n

darab

X

-ből és

n

darab

Y

-ból álló sorozatok száma

(\binom{2 n}{n})

. Ezek közül a nem

A

-típusúak valamilyen

k

-ra a

2 k

-adik betű után először (esetleg azután még más helyen is) kettévághatók úgy, hogy odáig

k

darab

X

és

k

darab

Y

legyen

(1 \leq k \leq n - 1)

. A vágás előtti rész

A

-típusú, az ilyenek száma

a_{k}

, tovább a

2 n - 2 k

elem

(\binom{2 n - 2 k}{n - k})

lehetséges elrendezésének bármelyike állhat. Ebből az

\begin{matrix} a_{n} = (\binom{2 n}{n}) - a_{1} (\binom{2 n - 2}{n - 1}) - a_{2} (\binom{2 n - 4}{n - 2}) - ... - a_{n - 1} (\binom{2}{1}) \end{matrix}

(2)

összefüggés adódik, ami az

a_{1} = 2

kezdő értékkel szintén meghatározza az

a_{n}

értékeket. Kézenfekvő gondolat volna ezután

(1)

-et teljes indukcióval megpróbálni bizonyítani

(2)

felhasználásával, ez azonban nem vezet eredményre. Többen megtalálták vagy megsejtették

a_{n}

, meghatározását binomiális együtthatók segítségével. Még ennek ismeretében sem könnyű bizonyítani az

(1)

azonosság helyességét, a versenyzőknek nem is sikerült.^{$^{*}$}

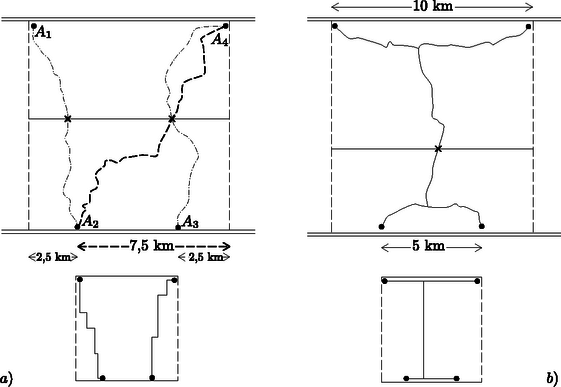
Harmadik feladat. Egy

10 km

-es oldalú négyzet alakú terület két párhuzamos oldalán autóút fut. A területen

4

megfigyelő állomás van. Úgy kell a négyzet oldalaival párhuzamos szakaszokból álló bekötő utakat építeni, hogy mindegyik állomásról el lehessen kerékpározni mindegyik autóúthoz. (Az autóutakon nem szabad kerékpározni.)
Bizonyítsuk be, hogy ez megoldható legfeljebb

25 km

-es úttal bárhol vannak is a megfelelő állomások, de rövidebbel nem mindig.

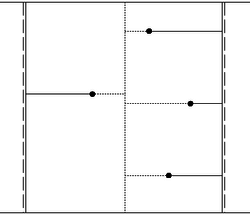
I. megoldás. Fusson a két autóút a terület északi és déli oldalán, és jelöljük a megfigyelő állomásokat nyugatról keletre haladva

A_{1}

A_{2}

A_{3}

A_{4}

-gyel, a négyzet nyugati határától mért távolságukat

a_{1}

a_{2}

a_{3}

a_{4}

-gyel. Ezek között egyenlők is lehetnek, ez esetben az állomások jelölése tetszőleges. Eszerint

a_{1} \leq a_{2} \leq a_{3} \leq a_{4}

.
Ha

a_{3} - a_{2} \leq 5 km

, akkor építsünk egy bekötőutat autóúttól autóútig

A_{2}

és

A_{3}

között, illetőleg a kettőn keresztül, ha

a_{2} = a_{3}

, továbbá mindegyik állomástól eddig az útig egy nyugat‐keleti bekötőutat. Az előbbi út hossza

10 km

, az

A_{1}

-től és

A_{4}

-től épített utak összhossza

a_{4} - a_{1} \leq 10 km

, az

A_{2}

-től és

A_{3}

-ból épített utaké

a_{3} - a_{2} \geq 5 km

a feltétel szerint. Az egész úthálózat hossza tehát legfeljebb

25 km

.
Ha

a_{3} - a_{2} \geq 5 km

, akkor építsünk egy‐egy észak‐déli bekötőutat

A_{1}

és

A_{2}

közt is, meg

A_{3}

és

A_{4}

között is, ill. a megfigyelőállomásokon át, ha

a_{1} = a_{2}

vagy

a_{3} = a_{4}

, továbbá

A_{1}

-ből és

A_{2}

-ből az elsőig,

A_{3}

-ból és

A_{4}

-ből a másodikig nyugat‐keleti bekötőutakat. Ennek az útrendszernek a hossza

\begin{matrix} 20 + a_{2} - a_{1} + a_{4} - a_{3} = 20 + (a_{4} - a_{1}) - (a_{3} - a_{2}) \leq 20 + 10 - 5 = 25 km, \end{matrix}

tehát ebben az esetben is van legfeljebb

25 km

-es úthálózat a kívánt tulajdonságokkal (1. ábra a) és b) része).

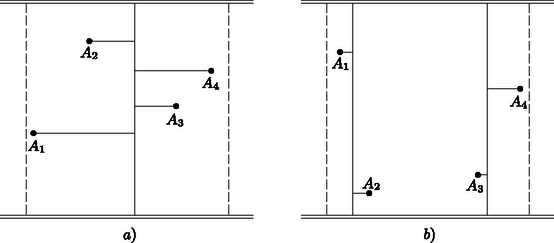1. ábra

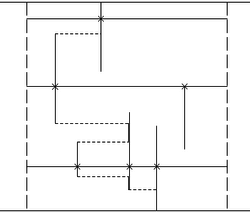
Megmutatjuk, hogy

25 km

-nél rövidebb úthálózattal nem oldható meg a feladat, ha pl. a megfigyelő állomások a terület határán vannak a délnyugati saroktól északra, az északnyugatitól keletre, az északkeletitől délre és a délkeletitől nyugatra

2, 5 - 2, 5 km

-re. Ebben a sorrendben jelöljük őket

A_{1}

A_{2}

A_{4}

A_{3}

-mal.
Egy legrövidebb úthálózat legfeljebb két egymással össze nem függő részből állhat, mert ha legalább háromból áll, akkor már az észak‐déli irányú útszakaszok legalább

30 km

-t tesznek ki. Ha két részből áll, akkor van legalább

20 km

-nyi észak‐déli szakasza. Ebben az esetben valamelyik rész legalább két állomást tartalmaz. Ha

A_{1}

-ből

A_{3}

-at vagy

A_{4}

-et, vagy

A_{4}

-ből

A_{2}

-t el lehet érni, akkor a nyugat‐keleti irányú szakaszok összesen legalább

7, 5 km

-t tesznek ki, ha pedig

A_{1}

-ből

A_{2}

-t,

A_{3}

-ból

A_{4}

-et lehet csak elérni, ehhez tegalább kétszer

2, 5 km

-nyi nyugat‐keleti irányú útszakasz szükséges.
Ha végül mindegyik állomásról bármelyikre el lehet jutni bekötőutakon haladva, akkor tekintsük az úthálózatnak

A_{1}

-ből

A_{4}

-be vezető részét és azt a pontot, ahol ezt

A_{2}

-ből, ill.

A_{3}

-ból először érhetjük el. Ha

A_{1}

-ből indulva előbb az

A_{2}

felé vezető elágazást érjük el, akkor van az úthálózatnak egy

A_{1}

A_{2}

közti és egy

A_{3}

A_{4}

közti része, amelyeknek nincs közös pontja; ezeknek legalább 7,5‐7,5 km-nyi észak‐déli szakasza van, az egész hálózat nyugat‐keleti szakaszai viszont legalább

10 km

-t tesznek ki. Ha viszont az

A_{3}

-ba vezető elágazást érjük el előbb, vagy négyes útkereszteződés van, akkor

A_{1}

A_{3}

és

A_{2}

A_{4}

közt van olyan összeköttetés, amelyeknek legfeljebb egy közös pontja van, és egész hasonlóan látható, hogy ekkor legalább

15 km

-nyi nyugat‐keleti és

10 km

-nyi észak‐déli útszakasz van (2. ábra a) és b) része). ‐ Evvel a feladatot teljes egészében megoldottuk.

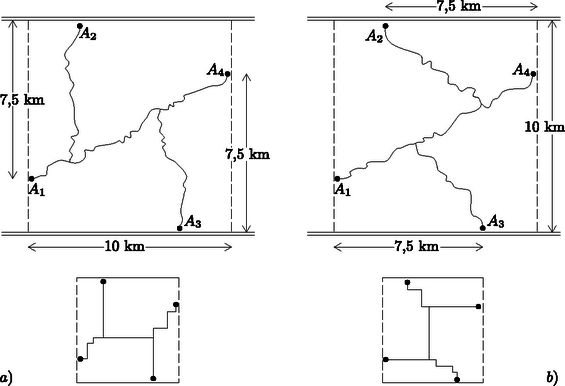2. ábra

Megjegyzés. A megoldás első része mutatja, hogy

25 km

-nél rövidebb útrendszer is van, ha

A_{1}

és

A_{4}

nem a terület nyugati és keleti határvonalán van, és akkor is, ha

a_{3} - a_{2}

nem éppen

5 km

. A megoldás ezen részében szereplő első útrendszerhez hasonló szerkeszthető az észak‐déli és nyugat‐keleti irány szerepének megcserélésével is, ami bizonyos feltételek mellett ismét

25 km

-nél nem hosszabb útrendszert szolgáltat. Ebből további szükséges feltételek lesznek leolvashatók.
Építsünk egy

n

nyugat‐keleti utat az egész területen át, amelyiktől két megfigyelő állomás északra van, kettő délre (esetleg két állomáson áthalad, a másik kettőt elválasztja, vagy legalább három állomáson áthalad). Ezután a legészakibb állomáson vagy az ilyenek egyikén át az északi autóúttól, a legdélibb állomáson vagy azok egyikén át a déli autóúttól

n

-ig észak‐déli bekötőutat építünk és a másik két állomástól

n

-ig szintén (3. ábra). Ha az utolsó két út hossza

b_{3}

és

b_{4}

, akkor az egész útrendszeré

20 + b_{3} + b_{4}

, és ez kisebb, mint

25 km

, ha

b_{3} + b_{4} < 5 km

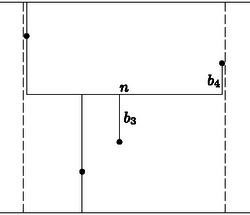3. ábra

Ha az

n

-en keletkező északi elágazások és déli elágazások nem választják el egymást, akkor az úthálózat hossza

20 km

-re csökkenthető. Mozdítsuk el ugyanis

n

-nek a nyugati határtól a második elágazásig terjedő részét arra, amerre az elágazások vezetnek a közelebbi állomásig, és hasonlóan módosítsuk a harmadik elágazástól a terület határáig terjedő részét is. Az új útrendszer legföljebb

20 km

hosszú (4. ábra).

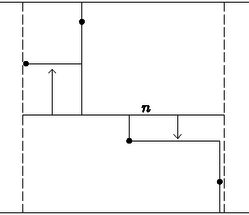4. ábra

Azt kaptuk tehát, hogy csak akkor nem elegendő

25 km

-nél rövidebb úthálózat, ha a következő feltételek teljesülnek:

a)

A terület nyugati és keleti határa mentén is legyen megfigyelőállomás;

b)

a területet egy észak‐déli és egy kelet‐nyugati vonallal felosztva úgy, hogy két állomás a vonaltól ne feküdjék keletre, a másik kettő ne nyugatra és hasonlóan a másik vonaltól kettő ne feküdjék délre, a másik kettő ne északra, akkor a keletkező négy téglalap egyike se tartalmazzon a belsejében és határán egynél több állomást;

c)

az említett kelet‐nyugati vonalhoz két oldalról legközelebb eső állomás e vonaltól vett távolságának összege éppen

5 km

legyen;

d)

az észak‐déli vonal két oldalán a legközelebbi állomások távolságának összege legalább

5 km

legyen.
A fenti megoldás második részének gondolatmenetével belátható, hogy ha mind a négy feltétel teljesül, akkor szükség is van mindig

25 km

-es úthálózatra.

II. megoldás. Két úthálózatot tervezünk és utólag választjuk ki a kedvezőbbet. Az egyiknek két észak‐déli útszakasza lesz a terület két határán, a másiknak egy a terület középvonala mentén. (Az 5. ábrán az első úthálózat folytonos, a második pontozott vonallal van rajzolva.) Ezután minden megfigyelőállomástól kelet‐nyugati utat építünk a terület közelebbi határáig, ill. a középvonalig (a középvonalra eső esetleges állomástól tetszés szerint az egyik határig). Világos, hogy a pontozott útrendszeren is el lehet jutni minden állomástól bármelyik autóútig, a (két részből álló) folytonosan kihúzott útrendszer mentén is.

5. ábra

A két úthálózat együtt

30 km

észak‐déli és négyszer

5 km

kelet‐nyugati útszakaszból áll, tehát

50 km

hosszú, így legalább az egyik legfeljebb

25 km

-es. Ez (illetőleg bármelyik, ha a kettő egyenlő hosszú) kielégíti a feladat követelményeit.
Szükség van legalább

25 km

-nyi úthálózatra, ha pl. az

A_{1}

és

A_{2}

megfigyelő állomás a terület északnyugati és északkeleti sarkában van,

A_{2}

és

A_{3}

pedig a déli út mentén, a nyugati, ill. keleti határtól 2,5‐2,5 km-re.
Vizsgáljuk először egy, a feltételeket kielégítő bekötő-útrendszer észak‐déli útszakaszait. Ez összesen véges számú útszakasz, egy tetszés szerinti kelet‐nyugati egyenes ezeket véges számú pontban metszi; legalább egyben, mert ellenkező esetben volna olyan kelet‐nyugati egyenes, amelyen nem lehetne átjutni az északi úttól a déli felé.
Minden nyugat‐keleti egyenes első ilyen metszéspontját véve, ezek véges sok útszakaszt futnak be, amelyek összhossza

10 km

(6. ábra). Hasonlóan, ha minden nyugat‐keleti egyenes legalább két vagy három észak‐déli útszakaszt metsz, akkor a metszéspontok legalább

20

, ill.

30 km

-nyi észak‐déli útszakaszon futnak végig.

6. ábra

Az olyan útrendszerek kedvezőtlenek, amelyeknél mindegyik egyenes legalább

3

metszéspontot szolgáltat. Ha mindegyik egyenesen van legalább

2

metszéspont, de több nem mindegyiken, akkor szemeljünk ki egy egyenest, amelyen két metszéspont van. Mindegyik megfigyelő állomástól el kell tudni jutni valamelyik metszésponthoz, hogy eljuthassunk a nyugat‐keleti vonal másik oldalán levő autóúthoz. Ha

A_{1}

-ből és

A_{3}

-ból vagy

A_{2}

-böl és

A_{4}

-ből ugyanahhoz a metszésponthoz lehet eljutni, akkor a megfelelő két állomás közt van egy olyan útrész, amelyiknek legalább

7, 5 km

-nyi nyugat‐keleti szakasza van (7a ábra, szaggatott vonal); ha pedig

A_{1}

és

A_{2}

-ből az egyik metszéspont érhető el,

A_{3}

, és

A_{4}

-ből a másik, akkor van kétszer

2, 5 km

-nyi nyugat‐keleti útszakasz (7a. ábra, pontozott vonal), és mindkét esetben legalább

20 km

összhosszú észak‐déli útszakaszok, mint láttuk.
Ha végül van olyan nyugat‐keleti egyenes, amelyiken csak egy metszéspont van, akkor egy ilyen metszésponthoz mindegyik állomásról el lehet jutni (7b. ábra). Ekkor azonban az úthátózatnak az egyenestől északra eső része legalább

10 km

-nyi nyugat‐keleti útszakaszt tartalmaz, a déli része legalább

5 km

-nyit, ehhez járul legalább

10 km

-nyi észak‐ déli útszakasz. Mindig szükség van tehát legalább

25 km

-es úthálózatra.

7. ábra

Megjegyzések. 1. A megoldás első részének gondolatmenete Hangya László megoldása. Ez alkalmas sok további felmerülő kérdés megválaszolására is.
Ha pl.

4

helyett

5

vagy

6

megfigyelőállomás van a területen, akkor a fenti módon megszerkesztett két úthálózat összhossza

55

, ill.

60 km

lesz, így legfeljebb

27, 5

, ill.

30 km

hosszú úthálózattal megoldható a feladat.
2. Ugyanesak

30 km

-t ad korlátul

6

pont esetén a gondolat következő módosított alkalmazása is. Osszuk a területet

4

észak‐déli úttal

3

egyenlő széles részre és mindegyik megfigyelő állomástól az őt közrefogó két útig építünk merőleges bekötőutat. Minden második észak‐déli út a rá merőleges, csatlakozó útszakaszokkal alkotja az egyik útrendszert, a kimaradók a másikat. A két útrendszer összhosszára így

\begin{matrix} 4 \cdot 10 + 6 \cdot \frac{10}{3} = 60 km \end{matrix}

adódik, mint az előbbi esetben is.
Nem nehéz belátni, hogy legalább

30 km

-nyi útra szükség is van, ha a megfigyelő állomások pl. a terület két útmenti oldalának közepén és két szélén vannak.
3.

5

állomás esetén van mindig

27, 5 km

-nél rövidebb úthálózat is. A legjobb korlát megkeresését feladatul hagyom.
4. Hasonló okoskodással, alkalmasan választva azt is, hogy hány sávra osztjuk a területet,

n

pont esetén

(2 \sqrt[]{n} + 1) \cdot 5 km

, ill. annál kevéssel nagyobb felső korlát adódik a szükséges úthálózat hosszára.

^{$^{*}$}Lásd pl.: Hack Frigyes: Függvénytáblázatok ‐ Matematikai összefüggések, Tankönyvkiadó, Budapest, 1967. 75. old.

^{$^{*}$}Lásd a feladat megoldását K.M.L. 31 (1965), 24‐25. old.

^{$^{*}$}Lásd Matematikai Lapok 20 (1969), 150‐154. old.

^{$^{*}$}Először mindjárt az első $X$ után lesz ez a különbség 1.

^{$^{*}$}A kérdést feladatnak kitűzni tervezzük. (Szerk.)