| Cím: | Az optikai feladatok megoldásáról | ||
| Szerző(k): | Major János | ||
| Füzet: | 1982/január, 33 - 38. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
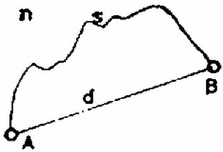
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az optikai feladatok megoldásáról Ebben a számunkban egy hosszabb optikai feladatsorozat kitűzését kezdtük meg. A sorozat célja eljutni olyan problémák megoldásához, melyek már aránylag közel állnak az optika gyakorlati hasznosításához, az optikai eszközökhöz. A feladatok egy részének megoldásakor sokat egyszerűsít a Fermat‐elv ismerete. Erről szól cikkünk első része. A második részben a vastag lencsékkel kapcsolatos alapvető fogalmakat foglaljuk össze, hogy a feladatokban ne csak a gyakorlati életben elő nem forduló "vékony'' lencsékre legyünk korlátozva. 1. A Fermat‐elv (legrövidebb idő elve) és a legképezési törvény Egy optikai elem (tükör, lencse stb.) esetén a képalkotást úgy szokás definiálni, hogy a képpont az a pont, ahol a megfelelő tárgypontból kiinduló összes (helyesebben sok, a tárgypontból egy bizonyos térszögben induló összes) fénysugár találkozik. A képalkotásnak ez a megfogalmazása szolgál alapul a képpontok megszerkesztéséhez, illetve ebből lehet levezetni a képalkotási törvényeket is, a lencse-, ill. tükörtörvényt. Ez utóbbihoz természetesen szükséges ismerni a különböző törésmutatójú közegek határán áthaladó fénysugár törési vagy visszaverődési törvényét is. A törési (visszaverődési) törvényt helyettesíthetjük a Fermat‐elvvel: két pont között a fény mindig úgy halad, hogy útjához a lehető legkevesebb időre legyen szüksége. Ennek segítségével egyszerűen megfogalmazhatjuk a leképezés feltételét is. Mivel a leképezésben részt vevő fénysugarak valamennyien a tárgypontból indulnak és a képpontba érkeznek, útjukhoz egyenlő időre van szükség, mert különben a Fermat‐elv szerint a legrövidebb időt igénylő sugármenet jöhetne csak létre. Alkalmazzuk a Fermat‐elvet, először a legegyszerűbb esetre: fény haladása homogén törésmutatójú közegben. A fénysugár áthalad az és pontokon (l. az 1. ábrát), amelyek távolsága , a fény sebessége pedig , ahol a fény sebessége vákuumban, az abszolút törésmutató. Mivel a fény sebessége állandó (), ha az ponttól -ig megtett út , a szükséges idő így , ami akkor a legkisebb, ha , azaz a fénysugár az ponttól a -ig egyenes vonalban halad, ellentétben az 1. ábrán rajzolttal.
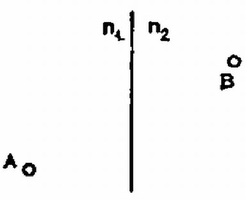
A 2. ábra olyan elrendezést mutat be, amelyben a törésmutató (azaz a fénysebesség) már nem homogén, hanem az egyik tartományban , a másikban , a két tartományt elválasztó felület pedig sík. Induljon a fénysugár az pontból és haladjon át a ponton is. Tudjuk, hogy a homogén törésmutatójú térrészben a fénysugár útja egyenes. Így egyetlen ismeretlenünk van, a határfelületen levő pont helyzete, ahol a fénysugár áthalad (3. ábra). Célszerű az és pontok helyzetét, illetve a pont hozzájuk viszonyított helyzetét az és a szögekkel jellemezni (3. ábra). Legyen továbbá az pont távolsága a határsíktól , a ponté . A fénysugár sebessége az törésmutatójú közegben , az törésmutatójúéban . Így az út befutásához szükséges idő két részből áll: 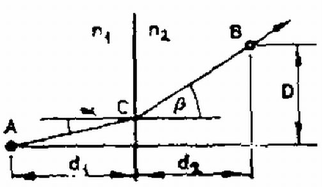 3. ábra Keressük minimumát és függvényében, de még a Általában könnyebb a dolgunk, ha a Fermat‐elvet egyszerű optikai elemek leképezésének vizsgálatára használjuk. Tekintsük például a domború tükör képalkotását. Legyen a tükör sugara , a tükör optikai középpontjának és a tárgypontnak a távolsága , a képpont -től mért távolsága pedig (4. ábra). Tekintsük u 4. ábrán megrajzolt feltételezett sugármenetet. Erre a fény haladási idejének meghatározásához számítsuk ki először az utakat. Legyen az pont távolsága az optikai tengelytől . Ekkor 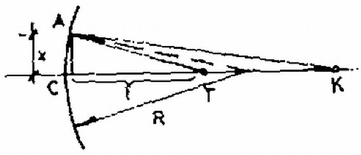 4. ábra Így ahol az utolsó átalakítást azzal a feltételezéssel hajtottuk végre, hogy , és . Hasonlóképpen Nézzünk meg egy másik, hasonló példát: vizsgáljuk meg egy vékony lencse leképezési törvényét. Legyenek a lencse felületének görbületi sugarai és (5. ábra). 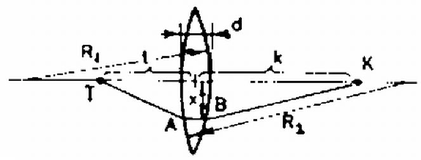 5. ábra Keressük a tárgypont képét, tegyük fel, hogy az éppen a pont. Legyen és távolsága a lencsétől (vékony lencse: a lencse középvonalától) és . Mivel a lencse vékony (; ; ; ) és csak a fény útjának idejére vagyunk kíváncsiak, feltehetjük, hogy a fény a lencsén belül párhuzamosan halad a tengellyel (az eltérés elhanyagolhatóan kis hibát ad ‐ ezt a részletesebb számolás vagy átgondolás mutathatja ki). Legyen a fényút a út (5. ábra), legyen az: és pontok távolsága az optikai tengelytől , továbbá legyen a lencse törésmutatója , a környezetéé 1. A fény sebessége így a lencsén kívül (fénysebesség vákuumban) a lencsén belül . Számítsuk ki először a úthosszat: Korábban már felhasználtuk, hogy . , most megint megtesszük. A leképezések feltétele, hogy együtthatója nulla legyen. Ezekből Ezen a néhány példán láttuk, hogyan kell használni a legkisebb idő elvét a leképezési összefüggések levezetésére. Sok esetben ez a legegyszerűbb, leggyorsabb számolási módszer, azonban nem mindig, néha más módszerrel hamarabb célhoz érhetünk. A Fermat‐elv ilyen típusú alkalmazásánál azonban alapvető fontosságú, hogy biztosan jól végezzük a közelítő számításokat. És éppen ezért ez az elv szemléletesen és kvantitatíven is megadja, hogy miért és mennyire jók a leképezési törvények. (Nagy rekesznyílásnál torz lehet a felvétel, ha fényképezünk!) II. A vastag lencsékről 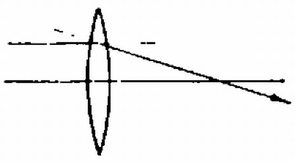 6. ábra Az optikai eszközökben a lencsék gyakran nem tekinthetők "vékony'' lencséknek, vastagságuk nem elhanyagolhatóan kicsi a görbületi sugarakhoz képest, rájuk az Vékony lencsénél -re adódik, azaz a tengellyel párhuzamosan beeső fénysugarak a fókuszpontban találkoznak. A fókuszpont ezen definícióját vastag lencsére is fenntartjuk. Ilymódon tetszőleges vastag lencsére egyszerűen meghatározhatjuk a fókuszpont helyét mindkét oldalon. A szórólencsénél is a vékony lencséknél megszokott módon járunk el, itt negatív előjelű lesz a fókusztávolság. Vékony lencséknél, ha a lencsébe behatoló és a lencsét elhagyó sugár hosszabbításait megrajzoljuk, azok éppen a lencsében (a lencse középvonalában) metszik egymást (l. a 6. ábrát). 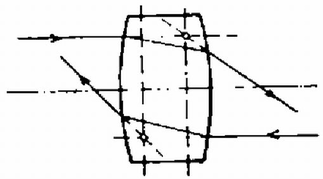 7. ábra Vastag lencsénél a metszéspont legtöbbször nem esik középvonalba (ha egyáltalán definiálható lencseközép [7. ábra]), sőt sok esetben a lencsén kívülre esik, és főleg pedig a jobbra és balra haladó fényre a metszéspontok különböző síkra esnek. Ezt a két síkot hívjuk a lencse fősíkjainak. Természetesen ezek össze is eshetnek egymással, vagy egészen furcsa helyekre is kerülhetnek. Ha azonban a tárgy és képtávolságot (továbbá a fókusztávolságot) a megfelelő fősíktól mérjük, továbbra is használhatjuk az A fősíkok bevezetése és az azokkal való számolás természetesen nem oldja meg a lencsék leképezésének hibáit. Továbbra is csak a tengelyhez képest kis szögben hajló sugarakat engedhetünk meg, fellépnek a nagy szögből eredő leképezési hibák, a színhibák, de nem lép fel az a hiba, hogy a kis beesési szög ellenére is a tengelytől más távolságra hagyja el a lencsét a fénysugár vastag lencséknél. Ez azt jelenti, hogy az 5. ábrán az szakaszt nem vehetjük többé párhuzamosnak a tengellyel (, többé nem teljesül), hanem hajlásának lényeges szerepe lehet. A fősíkok bevezetésével éppen ezt vesszük figyelembe. A fősíkok esetleges aszimmetrikus elhelyezkedése miatt a lencse nem lesz többé feltétlenül szimmetrikus: ez nem is meglepő, mert ha két "vékony'' lencsét egymás közelébe helyezünk, "vastag'' lencsét kaphatunk, ilyen pl. a távcső, nem mindegy, hogy melyik végén nézünk bele. A vastag lencsék (lencserendszerek) számolásához az eddig ismert módszereket vagy a Fermat‐elvet használhatjuk. A feladat dönti el, hogy melyik módszer a legcélravezetőbb, de mindenképpen a fősíkok meghatározása a legfontosabb feladat. Ehhez pedig legjobb a párhuzamosan beeső sugarak törését vizsgálni, vagy a leképezési törvényt átalakítani az ismert egyszerű összefüggések alakjára alkalmas fősíkok megválasztásánál. Major János |