Cím: Olimpiai előkészítő feladatok (Geometria II.)
Szerző(k):  Surányi László 
Füzet: 1984/december, 458 - 460. oldal  PDF  |  MathML 
Témakör(ök): Nemzetközi Matematikai Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Szerkesszünk adott n-szögbe olyan minimális kerületű n-szöget, amelynek csúcsai rendre az adott n-szög oldalegyenesekre esnek. (Az oldalegyenesek sorrendje azonos a csúcsokéval.) Bizonyítsuk be, hogy ha n=4 és az adott négyszög húrnégyszög, akkor kerületének bármely pontja lehet ilyen minimális kerületű, négy csúcsával a négy oldalegyenesre illeszkedő négyszög csúcspontja. Jellemzi-e ez a tulajdonság a húrnégyszögeket?

 

2. Bizonyítsuk be, hogy ha a,b,c egy háromszög oldalai, fa,fb,fc a hozzá tartozó szögfelezők hossza, akkor
1a+1b+1c≤32(1fa+1fb+1fc).

Mikor áll fenn egyenlőtlenség ? Igaz-e az állítás szögfelezők helyett súlyvonalakra is?
 

3. Bizonyítsuk be, hogy ha a,b,c a háromszög oldalai, sa,sb,sc a megfelelő oldalhoz tartozó súlyvonalak hossza, akkor
3[a2(b+c-a)+b2(c+a-b)+c2(a+b-c)]≤9abc≤4asa2+4bsb2+4csc2.

Mikor áll fenn egyenlőtlenség ?
 

4. Az AB szakasznak ugyanazon a partján két körív van adva. A külső körívén végigfut egy P pont. P melyik helyzetében lesz minimális a PA és PB egyenes által a belső körívből levágott két körszelet együttes területe?
 

5. Adott négy pont a síkon, bármely három által meghatározott háromszög területe legföljebb egységnyi. Igazoljuk, hogy a négy háromszög beírt köre közül a legkisebbnek legföljebb 2-1 a sugara. Mikor lehet egyenlőség? Igaz-e ugyanez, ha azt követeljük meg, hogy a négy pont közül bármely kettő távolsága legföljebb kettő legyen?
 

6. A k kör AB átmérőjének egy P pontjában merőlegest állítunk AB-re. A merőleges egy S pontját összekötjük az átmérő közelebbi végpontjával, B-vel. BS a k kört Z-ben metszi másodszor, ZP pedig Q-ban. Melyik a nagyobb a QP és a BS szakaszok közül?
 

7. Az ABC háromszög AB oldalához írt kör érintse az AB oldalt D-ben, az AC oldalegyenest E-ben. Az AC oldalhoz írt kör érintse az AC oldalt F-ben. BF és CD egyenesek N metszéspontján keresztül húzzunk párhuzamost AC-vel, az A csúcson keresztül pedig BF-fel. Bizonyítsuk be, hogy ez a két egyenes a DE egyenesen metszi egymást.
 

8. Az ABC háromszög beírt köre az AB,AC,BC oldalakat rendre a D, E, F pontokban érinti. EF az AB egyenest P-ben metszi. P-ből a körhöz húzott másik érintő D'-ben érinti a kört. Igazoljuk, hogy D, D', C kollineáris. (Feltesszük, hogy AC≠BC.)
 

9. Igazoljuk, hogy az előző feladat jelöléseit alkalmazva, AF és BE egyenes G metszéspontjának a három oldaltól vett x,y,z távolságára
x:y:z=11+cosα:11+cosβ:11+cosγ,
ahol α,β,γ a háromszög szögei.
 

10. Az előző két feladat jelöléseit alkalmazva, adott az ABC háromszög beírt köre, a D érintési pont és az AF,BE egyenesek G metszéspontja. Szerkesszük meg a háromszöget.
 

11. Adott a síkon három, közös pontból induló félegyenes, a,b,c és adott három pont, P,Q,R. Szerkesszük meg azt a háromszöget, amelynek három oldala a három adott pontra, a három csúcsa a három adott félegyenesre illeszkedik.
 

12. Az ABC háromszög köré írt kör B és C pontbeli érintője a P pontban találkozik. Igaz-e, hogy ha a PA egyenest tükrözzük a BAC szög felezőjére, a kapott egyenes átmegy az ABC háromszög súlypontján ?
 

13. Húzzunk párhuzamost a parabola tengelyével két érintőjének, e-nek és f-nek A metszéspontjából. Legyen ez a párhuzamos g, a parabola fókusza F. Bizonyítsuk be, hogy FA és f szöge egyenlő e és g szögével.
 

14. Az egymásra merőleges OX és OY egyenesen fut az A, ill. a B pont úgy, hogy OA+OB állandó. Az O-n átmenő, AB-vel párhuzamos egyenes az ABO háromszög köré írt kört másodszor az M pontban metszi. Mi az M pont mértani helye ? Milyen alakzatot burkol az AB szakasz mozgás közben ?
 

15. Malfatti olasz matematikustól származik a következő feladat: Adott ABC háromszögben szerkesszünk egymást érintő k1, k2, k3 köröket úgy, hogy k1 érinti az AB, AC oldalakat, k2 érinti az AB, BC oldalakat és k3 érinti az AC, BC oldalakat. Steiner német matematikus Malfatti feladatára a következő megoldást adta: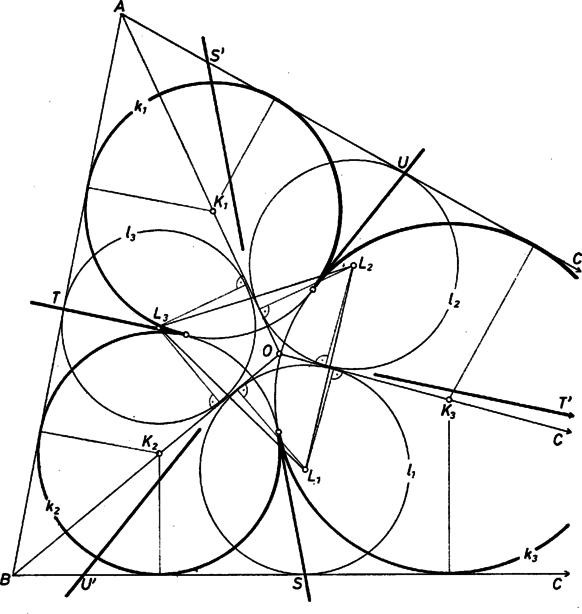
 
 

,,Legyen O az ABC beírt körének középpontja, l1,l2,l3 legyen a BOC, COA, AOB háromszög beírt köre. Húzzuk meg e három kör közül bármely kettőnek a másik belső közös érintőjét, messék ezek az oldalakat rendre az S, S', T, T', U, U' pontokban (l. az ábrát). Az ATT', BUU', CSS' háromszögek beírt köre megfelel k1, k2, k3 körnek.''
Helyes-e Steiner megoldása ?