Cím: Megjegyzések az olimpia 6. feladatához
Szerző(k):  Harcos Gergely 
Füzet: 1991/november, 344 - 347. oldal  PDF  |  MathML 
Témakör(ök): Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):Feladatok megoldásai: 1991/november: 1991. évi Nemzetközi Matematika Diákolimpia 23. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. (2)-ben γ=2-vel α=32+2(<3) is megfelelő, ez (3)-hoz hasonlóan igazolható.
Felvetődik a kérdés, hogy (2)-ben α meddig csökkenthető. Könnyen látható, hogy ha valamilyen α-hoz létezik a (2)-t kielégítő γ, akkor olyan γ is létezik, amely a [0;1] intervallumba esik (γ ugyanis pontosan akkor megfelelő α-hoz, ha {γ} is az).
Az is látszik, hogy a rögzített q(>0) nevező esetén (2)-nek elegendő teljesülnie arra a pq törtre, amelyik a lehető legjobban megközelíti a γ-t.
Feltehetjük, hogy 0≤γ<1, azaz 0q≤γ<qq, vagyis pq-ról feltehető, hogy a [0;1] intervallumba esik.
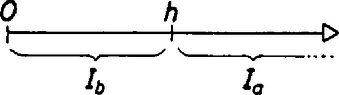
Ezek szerint pontosan azokhoz az α-khoz létezik "jó" γ, amelyekre a
(pq-1αq2;pq+1αq2)
alakú nyílt intervallumok 0≤p≤q, 0<q, p és q egészek) nem fedik be a [0;1)-et. (Természetesen itt a [0;1) intervallum helyett [0;1]-et is írhatunk, mert az (1-1α;1+1α) fedőintervallum tartalmazza az 1-et.)
A kérdés tehát az, hogy milyen kicsi lehet az α, ha
[0;1]/⊂⋃p,q∈N0≤p≤q≠0(pq-1αq2;pq+1αq2),(5a)
illetve kontraponálva, milyen nagy lehet az α, ha
[0;1]⊂⋃p,q∈N0≤p≤q≠0(pq-1αq2;pq+1αq2).(5b)
Az (5a)-t, ill. az (5b)-t kielégítő (pozitív) α-k egy-egy Ia, ill. Ib intervallumot alkotnak úgy, hogy Ia∩Ib=0,Ia∪Ib=(0,+∞) és
supIb=infIa=h.
Nyilván (0;h)⊂Ib,(h;+∞)⊂Ia.
 
 

Egyszerűen adódik, hogy 2,5≤h, azaz 2,5∈Ib. Ehhez azt kell csak megmutatnunk, hogy α=2,5 esetén (5b) teljesül, amit pedig igazol a
[0;1]=[0;0,4)∪{0,4}∪(0,4;0,6)∪{0,6}∪(0,6;1]⊂
⊂(-12,5;12,5)∪(410-12,5⋅102;410+12,5⋅102)∪
∪(12-12,5⋅22;12+12,5⋅22)∪(610-12,5⋅102;610+12,5⋅102)∪
∪(1-12,5;1+12,5)⊂⋃p,q∈N0≤p≤q≠0(pq-12,5q2;pq+12,5q2)
reláció.
Ezek szerint (2)-ben α<2,5 már nem lehetséges
Most példát adok α=3+52≈2,618-ra. Legyen γ=5-12; azt fogjuk belátni, hogy
|5-12-pq|≥1aq2,(6)
azaz
|γ-pq|≥1aq2.

Mivel 0<γ<1, ezért az előzőek alapján (6)-ban feltehetjük, hogy 0≤pq≤1.
Jelölje γ¯aγ algebrai konjugáltját: γ¯=-5-12. Ekkor γ és γ¯ az
x2+x-1=0
egyenlet gyökei, és ezért tetszőleges x számra
x2+x-1=(x-γ)⋅(x-γ¯).

Emiatt
|pq-γ|⋅|pq-γ¯|=|(pq)2+(pq)-1|=|p2+pq-q2|q2.

A bal oldalon 0≤pq≤1 alapján
(0<)|pq-γ¯|=|pq+5+12|=pq+5+12≤1+5+12=5+32=α,
a jobb oldalon pedig |p2+pq-q2|≥1, hiszen |p2+pq-q2|=0 esetén a bal oldal egyik tényezője eltűnne, ami lehetetlen, mert γésγ¯ irracionálisak. Így
α⋅|pq-γ|≥1q2,
azaz
|γ-pq|≥1αq2,
amit bizonyítani akartunk.
Levezetésünkből az is kiderül, hogy (6)-ban pontosan akkor érvényes az egyenlőség, ha p=1ésq=1.
A (2)-t kielégítő α-k alsó határa ‐ h ‐ tehát a [2,5;5+32] intervallumba esik.
 
2. Előző megjegyzésünk szerint tudunk olyan (xk) sorozatot készíteni, amelyre a β=5+34≈1,309 korláttal
|xk|<β,és|xi-xj|⋅|i-j|≥1(7)
teljesül. Itt is jó kérdés az, hogy milyen kicsi lehet a β.
 
Megmutatjuk, hogy 1<β; azaz β≤1 már nem lehetséges.
Legyen (xk) egy, a (7)-et kielégítő sorozat, és tegyük fel, hogy az i0,i1,...,in∈N indexekre
(-β<)xi0<xi1<...<xin(<β).

Ekkor (7) szerint
2β>xin-xi0=∑s=1n(xis-xis-1)≥∑s=1n1|is-is-1|,
tehát
1|in-in-1|+1|in-1-in-2|+...+1|i1-i0|<2β.(8)

Ha most x0,x1,x2,x3ésx4 lehetséges nagyságbeli sorrendjeit vizsgáljuk, akkor ‐ nem túlságosan nehéz ellenőrizni ‐
a) vagy van három olyan 0≤i0,i1,i2≤4 index, hogy xi0<xi1<xi2, és
|i1-i0|=1,|i2-i1|=1, tehát (8) alapján 2=11+11<2β, vagy pedig
b) van 4 olyan 0≤i0,i1,i2,i3≤4 index, hogy xi0<xi1<xi2<xi3, és
|i1-i0|=2,|i2-i1|=1,|i3-i2|=2, vagyis (8) alapján 2=12+11+12<2β.
Mindenképpen teljesül tehát a 2<2β,1<β egyenlőtlenség.
Ezek szerint a (7)-ben lehetséges β-k alsó határa az [1;5+34] intervallumban van valahol.
 
3. Láttuk, hogy a≥1 esetén létezik olyan korlátos (xk) sorozat (|xk|<β), amelyre
|xi-xj|⋅|i-j|a≥1(9)
teljesül minden i≠j természetes számpár esetén. Megmutatjuk, hogy a<1 esetén ilyen sorozat nem létezik.
Tegyük fel ugyanis, hogy állításunkkal ellentétben az (xk) sorozatra |xk|<β és (9) teljesül. A sorozat korlátos volta miatt vannak egymáshoz tetszőlegesen közel lévő elemek, tehát van olyan i≠j természetes számpár, amelyre |xi-xj|<1 teljesül, és ekkor (9)-ből |i-j|a>1, vagyis a≤0 semmiképpen nem lehetséges. A továbbiakban legyen tehát 0<a<1. Tekintsük az x0, x1, ..., xn elemek nagyságbeli sorrendjét:
xi0<xi1<...<xin,
ahol (i0,i1,...,in) a (0,1,...,n) elemek egy permutációja. Ekkor (8)-hoz hasonlóan (9)-ből
∑s=1n|is-is-1|-a<2β.(10)

Mivel 0≤is,is-1≤n, ezért 1≤|is-is-1|≤n(s=1,2,...,n), vagyis
|is-is-1|-a≥n-a,
hiszen 0<a miatt az x↦x-a függvény szigorúan csökkenő. Ezt (10)-zel egybevetve
2β>∑s=1n|is-is-1|-a≥∑s=1nn-a=n⋅n-a=n1-a.

Azt kaptuk tehát, hogy tetszőleges n természetes számra
2β>n1-a,
ami ellentmondás, mert 0<1-a miatt a jobb oldal minden határon túl nő. Ezzel állításunkat beláttuk.
 
Eredményeinket a következőképpen foglalhatjuk össze.
a) Ha a≥1, akkor létezik olyan (xk) sorozat, amelyre valamilyen 0<β korláttal |xk|<β(k=0,1,...), továbbá i≠j(i,j∈N) esetén |xi-xj|⋅|i-j|a≥1 teljesül
b) Ha a<1, akkor ilyen sorozat nem létezik.
c) Az a=1-re megadott sorozat minden a≥1-re megfelelő, a=1-re meg tudunk adni olyan sorozatot, amelynek korlátja β=5+34(≈1,309).
Fent közölt módszerünkkel β<54(=1,25) már nem érhető el.
Nincs olyan sorozat, amelynek korlátja β≤1 lenne.
Kérdés, hogy hol a határ az 1 és a 5+34 között.