Cím: The centre of gravity of a triangle
Szerző(k):  Imre Légrádi 
Füzet: 2003/októberi melléklet, 51 - 53. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

If the distribution of mass is considered, there are three different configurations that we can call triangle. Zero-dimensional triangles consist of three non-collinear pointlike objects of finite masses. Three thin rods of uniform mass distribution form a one-dimensional triangle. Finally, a two-dimensional triangle is a thin triangular sheet of uniform mass distribution. It is true for each of the three types of triangle that if it is situated on the surface of the Earth and its size is small relative to the radius of the Earth then its centre of gravity coincides with its centre of mass.
In geometry, the centroid of a triangle is the point where the medians intersect. The centroid is related to the concept of the centre of mass, but they are not the same. In physics, it makes a difference whether the triangle is zero, one- or two-dimensional.
In order to find the centre of mass of a zero-dimensional triangle, the centre of mass of two point masses is found first (i.e. the point that divides the line segment joining them in an inverse ratio to the masses); then by assuming that the total mass of the two points is concentrated at that point, the centre of mass of that point and the third point is located. In that case, depending on the three masses, the centre of mass of the triangle may be anywhere inside the geometrical triangle formed by the three points. The centre of mass only coincides with the centroid if the masses of the three points are equal.
The centre of mass of a two-dimensional triangle can be determined by a similar procedure based on cutting up the triangular plate into narrow bands. The details can be found in physics books. In this case, too, the centre of mass is found to coincide with the centroid of the geometrical triangle.
The case of the one-dimensional triangle made up of thin rods, however, is not so simple. Since competition problems in physics often feature triangles constructed out of this rods, sticks or wires (see the Hungarian National Competition of the year 2000/2001), let us investigate this type of triangle in greater detail.

 

Consider a triangle that consists of such rods of uniform cross-sectional area, equal density and uniform mass distribution. Let the lengths of the sides be a=BC, b=CA and c=AB where a≥b≥c (Figure 1). The procedure of finding the centre of mass can be reduced to the zero-dimensional case. The centre of mass of each side (rod) is at its midpoint, and the corresponding mass is proportional to the length of the side. Thus we can assume that there is a mass of k⋅a at point D, a mass of k⋅b at point E, and a mass of k⋅c at point F. The centre of mass of the resulting zero-dimensional triangle coincides with that of the original one-dimensional triangle. The centre of mass of the masses at E and F is the point G of the line segment EF that divides EF in inverse ratio to the masses, that is,
GFGE=k⋅bk⋅c.
The right-hand side of the proportion can also be written in the form b2:c2, which means that G divides EF in the ratio of the length of the side DF of the triangle DEF to side DE. This is the ratio in which the bisector of the angle at D divides the opposite side, hence the line DG bisects the angle DEF.
Thus the centre of mass of the zero-dimensional triangle DEF lies on the angle bisector DG. Since we could have also started with the point masses k⋅a and k⋅c concentrated at the points D and F, and obtained that the centre of mass of the zero-dimensional triangle DEF lies on the angle bisector of the angle at C, the centre of mass must be the intersection of the angle bisectors, that is, the centre of the inscribed circle of the triangle DEF.
Therefore, the centre of mass of the one-dimensional triangle is not the centroid defined in geometry but the centre of the inscribed circle of the triangle of midlines.
It is also known from geometry that the centroid of a triangle is closest to the longest side. It can be shown that the centre of mass of the one-dimensional triangle is also closest to the longest side. What is more, we shall prove below that the centre of mass of the one-dimensional triangle is closer to the longest side (if there is a longest side) than the intersection of the medians of the triangle, i.e. the centroid defined in geometry, and the two distances are only equal if the triangle is equilateral.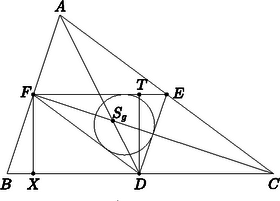
 

Figure 2 shows two medians (AD and CF) of the triangle ABC, the centroid Sg, and the altitude DT=FX drawn to the longest side of the triangle of midlines. It is known from geometry that the radius of the incircle of the triangle DEF is r=t/s where t is the area of the triangle and s is half the perimeter. Thus
t=a2⋅DT2=a⋅DT4
where DT if the altitude drawn to the longest side EF=a2, and
s=a2+b2+c22=a+b+c4.

We have seen that the centre of mass of the original one-dimensional triangle ABC is at a distance of DT-r from the longest side BC. The distance of the centroid from the same side is 23⋅XF=23⋅DT, since medians divide each other in a 1:2 ratio. We state, therefore, that DT-r≤23⋅DT. To prove this, substitute the expression
r=ts=a⋅DTa+b+c
obtained above into the left-hand side of the inequality. Dividing both sides by the non-zero quantity DT, we obtain that 1-aa+b+c≤23. Since a is the longest side of the triangle, the value of the left-hand side is at most 23. Equality only occurs if a=b=c, that is when the triangle is equilateral. That completes the proof.
It can be proved similarly that the centre of mass of the one-dimensional triangle is farther away from the shortest side c than the centroid. As for the middle side b, the centre of mass of the one-dimensional triangle may be farther away or closer than the centroid, or the two distances may even be equal if b=(a+c)/2. That was the case in problem 4, category II of the Hungarian National Competition in Physics, 2000/2001. Here is the problem:
 

The sides a, b, c of a right-angled triangle are thin rods of the same material, with rigid joints at the vertices. The triangle is in a vertical plane, its side b lying on a horizontal surface. The triangle falls from this unstable equilibrium.
a) Find the speed of the vertex B when it strikes the horizontal surface, given that the triangle does not slide while falling. (The triangle can turn without friction about the fixed side b.)
b) Where and with what speed would the vertex B strike the horizontal surface if the side b were free to slide and all friction were negligible? (a=30cm, c=50cm.)
 
A lot of solvers assumed automatically that the centre of mass was at the centroid. That was wrong. The centroid is at a distance of 10 cm from the side b=40cm. The true centre of mass of the triangle does not coincide with the centroid, but its distance from the side is also 10 cm. That is why this principal error did not influence the result of further calculations. The coincidence occurred because the length of b happened to be the arithmetic mean of the other two sides. If the longest side c=50cm had been lying on the plane, the confusion of the centroid and the true centre of mass would have caused a numerical error, too (they would have calculated with 8 cm instead of the correct distance of 7 cm).
An interesting generalization of the problem is obtained by considering a zero-dimensional tetrahedron of four point masses, a one-dimensional tetrahedron constructed out of thin rods, a two-dimensional one made of thin plates, and finally a solid three-dimensional tetrahedron. Finding the centres of mass of these configurations is left to the reader as an exercise.