Cím:	Dániel Arany Competition in Mathematics, 2001/2002
Füzet:	2003/októberi melléklet, 19 - 21. oldal	PDF  |  MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Second round   1. Solve the following simultaneous equations on the set of integers: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle ab+cd}& {\displaystyle =-1}\hfill \\ \hfill {\displaystyle ac+bd}& {\displaystyle =-1}\hfill \\ \hfill {\displaystyle ad+bc}& {\displaystyle =-1}\hfill \end{array}}}\end{array}$   2. In a right-angled triangle of legs $a$ and $b$, the altitude drawn to the hypotenuse equals one fourth of the hypotenuse. Evaluate $\begin{array}{c}{\displaystyle {\left(\frac{a}{b}\right)}^6+{\left(\frac{b}{a}\right)}^6\mathrm{.}}\end{array}$   3. Prove that if $\begin{array}{c}{\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}}\end{array}$ for the real numbers $a$, $b$, $c$ then $\begin{array}{c}{\displaystyle \frac{1}{a^{1001}}+\frac{1}{b^{1001}}+\frac{1}{c^{1001}}=\frac{1}{a^{1001}+b^{1001}+c^{1001}}\mathrm{.}}\end{array}$   4. The diagonals $AC$ and $BD$ of a convex quadrilateral $ABCD$ are perpendicular. From the midpoint $K$ of side $AB$, drop a perpendicular onto the line of side $DC$. Let $P$ denote the foot of the perpendicular. From the midpoint $L$ of side $AD$, drop a perpendicular onto the line of side $BC$ and denote its foot by $Q$. Prove that the lines $KP$ and $LQ$ intersect on the line of diagonal $AC$.   Third round (final)   1. How many $n$-digit positive integers are there (in base 10), the sum of whose digits is $n^3-40$, where $n$ is a positive integer?   2. In a triangle $ABC$, $BC<CA<AB$. The perpendicular bisectors of side $BC$ and side $AC$ intersect the line of the altitude drawn from vertex $C$ at the points $P$ and $Q$, respectively. Determine the largest angle of the triangle, given that $4CP\cdot CQ=A{B}^2$.   3. Consider the sequence $\mathrm{1,2,3,}\text{...}\mathrm{,2002}$. One may rearrange the sequence as follows: It is allowed to put the last number in any of the 1st, 2nd, 3rd, $\text{...}$, 2002nd places, provided that the number moved forward from the end never precedes a greater number than itself. The same procedure can be applied to the new sequence and repeated as long as it is possible. Prove that after each step, one of the $\left(2k-1\right)$th and the $2k$th terms of the sequence thus obtained will be even and the other will be odd, for all $1\le k\le 1001$.   Schools with advanced mathematics programme   First round   1. Prove that if $\begin{array}{c}{\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}}\end{array}$ for the real numbers $a$, $b$, $c$ then $\begin{array}{c}{\displaystyle \frac{1}{a^{1001}}+\frac{1}{b^{1001}}+\frac{1}{c^{1001}}=\frac{1}{a^{1001}+b^{1001}+c^{1001}}\mathrm{.}}\end{array}$   2. A square of side $a$ is rotated about its centre, and thus a new square is obtained. The common part of the two squares is an equilateral octagon of side $b$. $a)$ Express the area of the octagon in terms of $a$ and $b$. $b)$ Prove that $\begin{array}{c}{\displaystyle \sqrt[]{t\cdot T}<a^2<\sqrt[]{\frac{t^2+T^2}{2}}}\end{array}$ where $t$ and $T$ denote the areas of the intersection and union of the two squares, respectively.   3. The lines of the sides of an equilateral triangle $ABC$ in the interior of a circle $k$ intersect the circle at the points $A_1$, $A_2$, $B_1$, $B_2$, $C_1$, $C_2$ as follows: The intersections of line $AB$ with the circle are $A_1$ and $B_2$, the intersections of $BC$ are $B_1$ and $C_2$, and the intersections of $CA$ are $C_1$ and $A_2$, as shown in the Figure. 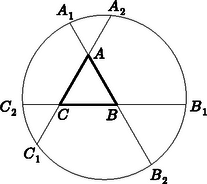  Prove that $\begin{array}{c}{\displaystyle A{A}_1+B{B}_1+C{C}_1=A{A}_2+B{B}_2+C{C}_2\mathrm{.}}\end{array}$   4. Given that the sum of 121 positive integers is 360, prove that it is possible to select some numbers out of the 121, such that their sum is 120.   Second (final) round   1. Prove that no matter what positive integer the base of the number system is, it is always true that if the ratio of the number $\overline{abc}$ to $\overline{cba}$ is 2 then $a+c=b$.   2. $P$ is a point inside or on the boundary of a regular polygon with $2k+1$ sides. Let $\begin{array}{c}{\displaystyle d_1\le d_2\le \text{...}\le d_{2k+1}}\end{array}$ denote the distances of $P$ from the vertices, in increasing order. For what point will $d_{k+1}$ be a maximum?   3. $N$ microchips can test one another as follows: If any two are connected, each of them will display whether the other is good or faulty. A good chip will always answer correctly while a faulty chip will give a random answer. Given that more than half of the chips are good, is it possible to select a good chip with certainty in less than $N$ trials?