Kezdőlap


Cím:	Ordering watermelons
Szerző(k):	Imre Légrádi
Füzet:	2003/októberi melléklet, 17 - 19. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A watermelon merchant has the following obsession: In the marketplace, he always lines up his perfectly spherical watermelons along the stone bench so that each melon touches its neighbors and the points where the melons touch the bench are collinear.

One morning, he arrived at the marketplace with eleven spherical watermelons in his car. Before he could line up the melons in the usual way, the marketplace inspector went up to him and measured the diameters of the melons to be

d_{1} = 16

cm,

d_{2} = 18

cm,

d_{3} = 22

cm,

d_{4} = 26

cm,

d_{5} = 28

cm,

d_{6} = 30

cm,

d_{7} = 34

cm,

d_{8} = 36

cm,

d_{9} = 38

cm,

d_{10} = 40

cm,

d_{11} = 42

cm. The inspector added up the diameters and declared that the merchant was to pay a fee for using a total length of 330 cm of the bench. The merchant did not accept this, saying that he was able to arrange his melons in a shorter line than that. Given the diameters, would the inspector please calculate the lengths of the shortest possible line of watermelons, and then he would pay for that. Pleased that the merchant also liked mathematics, the inspector agreed to calculate the shortest possible length, that is the diameter, as defined by combinatorial geometry, of the plane figure obtained by the union of the orthogonal projections of the appropriately arranged melons onto the table, provided that the merchant would prove that for the given radii

r_{1} \leq r_{2} \leq r_{3} \leq ... \leq r_{n - 1} \leq r_{n}

n

melons, this length is a minimum if the sum

\begin{matrix} \begin{matrix} D & = & {(\sqrt[]{r_{k_{1}}} - \sqrt[]{r_{k_{2}}})}^{2} + {(\sqrt[]{r_{k_{2}}} - \sqrt[]{r_{k_{3}}})}^{2} + {(\sqrt[]{r_{k_{3}}} - \sqrt[]{r_{k_{4}}})}^{2} + \\ + & {(\sqrt[]{r_{k_{4}}} - \sqrt[]{r_{k_{5}}})}^{2} + ... + {(\sqrt[]{r_{k_{n - 1}}} - \sqrt[]{r_{k_{n}}})}^{2} \end{matrix} \end{matrix}

is a maximum; where

r_{k_{1}}, r_{k_{2}}, r_{k_{3}}, ..., r_{k_{n - 1}}, r_{k_{n}}

are the radii of the consecutive melons touching each other, and the indices

k_{1}, k_{2}, k_{3}, ..., k_{n - 1}, k_{n}

denote a permutation of the numbers

1,2,3, ..., n - 1, n

resulting in the smallest length. Let us help them.

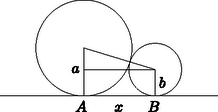
Solution: For two consecutive melons in the line, the distance between their points of tangency on the bench is

A B = x = 2 \sqrt[]{a b}

, where

a

and

b

are the radii of the two spheres (see the Figure 1.). Hence the length of the entire line of melons is

\begin{matrix} L = r_{l_{1}} + 2 \sqrt[]{r_{l_{1}} r_{l_{2}}} + 2 \sqrt[]{r_{l_{2}} r_{l_{3}}} + 2 \sqrt[]{r_{l_{3}} r_{l_{4}}} + ... + 2 \sqrt[]{r_{l_{n - 1}} r_{l_{n}}} + r_{l_{n}}, \end{matrix}

where

r_{l_{1}}, r_{l_{2}}, r_{l_{3}}, ..., r_{l_{n - 1}}, r_{l_{n}}

are the radii

r_{1} \leq r_{2} \leq r_{3} \leq ... \leq r_{n - 1} \leq r_{n}

of the melons in some order.

In the watermelon line of minimum length, the melons are arranged to make the above sum as small as possible.
Consider the sum of the diameters of the melons and denote it by

H

\begin{matrix} H = 2 (r_{1} + r_{2} + r_{3} + r_{4} + ... + r_{n_{1}} + r_{n}) . \end{matrix}

Subtract the sum

L

obtained above from

H

\begin{matrix} \begin{matrix} 2 (r_{1} + r_{2} + r_{3} + r_{4} + ... + r_{n - 1} + r_{n}) - \\ - (r_{l_{1}} + 2 \sqrt[]{r_{l_{1}} r_{l_{2}}} + 2 \sqrt[]{r_{l_{2}} r_{l_{3}}} + 2 \sqrt[]{r_{l_{3}} r_{l_{4}}} + ... + 2 \sqrt[]{r_{l_{n - 1}} r_{l_{n}}} + r_{l_{n}}) \end{matrix} \end{matrix}

The difference can be written as follows:

\begin{matrix} \begin{matrix} D & = & H - L = r_{l_{1}} - 2 \sqrt[]{r_{l_{1}} r_{l_{2}}} + r_{l_{2}} + r_{l_{2}} - 2 \sqrt[]{r_{l_{2}} r_{l_{3}}} + r_{l_{3}} + r_{l_{3}} - \\ - & 2 \sqrt[]{r_{l_{3}} r_{l_{4}}} + r_{l_{4}} + ... + r_{l_{n - 1}} - 2 \sqrt[]{r_{l_{n - 1}} r_{l_{n}}} + r_{l_{n}}, \end{matrix} \end{matrix}

which is the same as

\begin{matrix} D = {(\sqrt[]{r_{l_{1}}} - \sqrt[]{r_{l_{2}}})}^{2} + {(\sqrt[]{r_{l_{2}}} - \sqrt[]{r_{l_{3}}})}^{2} + {(\sqrt[]{r_{l_{3}}} - \sqrt[]{r_{l_{4}}})}^{2} + ... + {(\sqrt[]{r_{l_{n - 1}}} - \sqrt[]{r_{l_{n}}})}^{2} . \end{matrix}

The shortest line of melons is thus obtained by making this sum of squares a maximum. The task inflicted on the merchant by the inspector is thereby completed.
The task of the inspector, that is, finding the length of the shortest line of watermelons can be done in principle by considering all possible permutations of the 11 melons and selecting the shortest length. In practice, that would be really cumbersome, as there are

11! = 39 916 800

permutations. This part of the problem can also be solved with the help of the sum of squares obtained above: the sum of the squares of the differences between the square roots of the consecutive radii. It follows that the neighbours of melons of large radii should be melons of small radii.
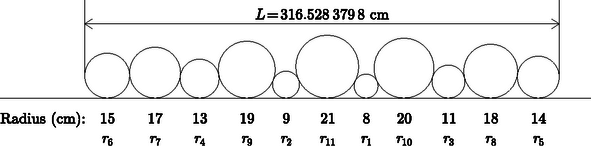
Let us, therefore, start with the largest melon placed in the middle, and let us put the two smallest melons right next to it on either side. Next to those, proceeding in both directions, let us place the two biggest of the remaining melons, followed by the two smallest that still remain, then the two biggest again and so on. Finally let us place the two medium-sized melons at the ends of the line. The procedure results in the following sequence of melons in Figure .

That is,

\begin{matrix} \begin{matrix} l_{1} = 6, l_{2} = 7, l_{3} = 4, l_{4} = 9, l_{5} = 2, l_{6} = 11, \\ l_{7} = 1, l_{8} = 10, l_{9} = 3, l_{10} = 8, l_{11} = 5. \\ \begin{matrix} L & = & r_{6} + 2 (\sqrt[]{r_{6} r_{7}} + \sqrt[]{r_{7} r_{4}} + \sqrt[]{r_{4} r_{9}} + \sqrt[]{r_{9} r_{2}} + \sqrt[]{r_{2} r_{11}} + \sqrt[]{r_{11} r_{1}} + \\ + & \sqrt[]{r_{1} r_{10}} + \sqrt[]{r_{10} r_{3}} + \sqrt[]{r_{3} r_{8}} + \sqrt[]{r_{8} r_{5}}) + r_{5} = 316.528 379 8 cm. \end{matrix} \end{matrix} \end{matrix}

With this arrangement, the value of the sum

\begin{matrix} Δ = | r_{l_{1}} - r_{l_{2}} | + | r_{l_{2}} - r_{l_{3}} | + | r_{l_{3}} - r_{l_{4}} | + ... + | r_{l_{n - 2}} - r_{l_{n - 1}} | + | r_{l_{n - 1}} - r_{l_{n}} | \end{matrix}

calculated for the whole line of melons is 79, and the sum

\begin{matrix} D = {(\sqrt[]{r_{l_{1}}} - \sqrt[]{r_{l_{2}}})}^{2} + {(\sqrt[]{r_{l_{2}}} - \sqrt[]{r_{l_{3}}})}^{2} + {(\sqrt[]{r_{l_{3}}} - \sqrt[]{r_{l_{4}}})}^{2} + ... + {(\sqrt[]{r_{l_{n - 1}}} - \sqrt[]{r_{l_{n}}})}^{2} \end{matrix}

13.471 620 2

cm, since

L + D = H

.
The above reasoning does not prove that this arrangement provides the shortest line of melons. We encourage the reader to find a proof or an even shorter line of the melons

...