Kezdőlap


Cím:	64. William Lowell Putnam Matematika Verseny - 2003
Füzet:	2004/április, 210 - 211. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A1. Legyen az $n$ adott pozitív egész szám. Hányféleképpen írható föl az $n$ pozitív egészek összegeként

\begin{matrix} n = a_{1} + a_{2} + ... + a_{k} \end{matrix}

alakban, ahol

k

tetszőleges pozitív egész úgy, hogy

\begin{matrix} a_{1} \leq a_{2} \leq ... \leq a_{k} \leq a_{1} + 1 ? \end{matrix}

Ha például

n = 4

, akkor négy ilyen felírás van: 4,

2 + 2

1 + 1 + 2

1 + 1 + 1 + 1

A2. Legyenek

a_{1}, a_{2}, ..., a_{n}

és

b_{1}, b_{2}, ..., b_{n}

nemnegatív valós számok. Bizonyítsuk be, hogy

\begin{matrix} {(a_{1} a_{2} \dots a_{n})}^{\frac{1}{n}} + {(b_{1} b_{2} \dots b_{n})}^{\frac{1}{n}} \leq {((a_{1} + b_{1}) (a_{2} + b_{2}) \dots (a_{n} + b_{n}))}^{\frac{1}{n}} \end{matrix}

A3. Határozzuk meg a

\begin{matrix} | sin x + cos x + tg x + ctg x + sec x + cosec x | \end{matrix}

kifejezés minimális értékét, ha

x

tetszőleges valós szám.

A4. Legyenek az

a

b

c

A

B

C

olyan valós számok, amelyekre

a \neq 0

A \neq 0

, továbbá minden valós

x

-re teljesül, hogy

\begin{matrix} | a x^{2} + b x + c | \leq | A x^{2} + B x + C | . \end{matrix}

Bizonyítsuk be, hogy ekkor

\begin{matrix} | b^{2} - 4 a c | \leq | B^{2} - 4 A C | . \end{matrix}

A5. Egy

2 n

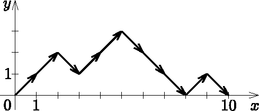
hosszúságú Dyck töröttvonal az origóból indul,

n

darab

(1; 1)

és

n

darab

(1; - 1)

valamilyen sorrendben egymáshoz csatlakozó lépésből áll úgy, hogy a töröttvonalnak nincsen pontja az

x

-tengely alatt. Egy ilyen töröttvonalban visszatérésnek nevezzük lefelé haladó lépéseknek az

x

-tengelyre érkező egymáshoz csatlakozó maximális sorozatát. Az ábrán látható 10-hosszúságú Dyck töröttvonal például két visszatérést tartalmaz, egyikük hossza 3, a másikuké pedig 1.

Bizonyítsuk be, hogy ha

n

páros, akkor kölcsönösen egyértelmű megfeleltetés létesíthető a

2 (n - 1)

hosszúságú és a visszatérés nélküli

2 n

hosszúságú Dyck töröttvonalak között.

A6. Nemnegatív egész számok egy adott

S

halmazára jelölje

r_{S} (n)

azon

(s_{1}; s_{2})

rendezett párok számát, amelyekre

s_{1} \in S

s_{2} \in S

s_{1} \neq s_{2}

, továbbá

s_{1} + s_{2} = n

. Felosztható-e a nemnegatív egész számok halmaza két részhalmazra, az

A

-ra és a

B

-re úgy, hogy minden

n

-re fennálljon az

r_{A} (n) = r_{B} (n)

egyenlőség?

B1. Léteznek-e olyan

a (x)

b (x)

c (y)

d (y)

polinomok, amelyekre az

\begin{matrix} 1 + x y + x^{2} y^{2} = a (x) c (y) + b (x) d (y) \end{matrix}

egyenlőség azonosan teljesül?

B2. Legyen az

n

adott pozitív egész szám. Az

1, \frac{1}{2}, \frac{1}{3}, ..., \frac{1}{n}

sorozatból kiindulva készítsük el az alábbi

(n - 1)

-tagú sorozatot:

\begin{matrix} \frac{3}{4}, \frac{5}{12}, ..., \frac{2 n - 1}{2 n (n - 1)} . \end{matrix}

Ebben a sorozatban minden egyes elem az előző sorozat két szomszédos elemének az átlaga. Ismételjük meg ezt az átlagolási eljárást a kapott sorozatra is, az így adódó

(n - 2)

-tagú sorozatra szintén, és folytassuk egészen addig, amíg a kapott ,,sorozat'' már csak egyetlen számból áll. Bizonyítsuk be, hogy ez a szám kisebb, mint

\frac{2}{n}

B3. Bizonyítsuk be, hogy minden pozitív egész

n

számra

\begin{matrix} n! = \prod_{i = 1}^{n} lkkt {1,2, ..., [\frac{n}{i}]} . \end{matrix}

(A feladatban ,,lkkt'' a legkisebb közös többszöröst,

[x]

x

szám egész részét jelenti.)

B4. Legyen

\begin{matrix} f (z) = a z^{4} + b z^{3} + c z^{2} + d z + e = a (z - r_{1}) (z - r_{2}) (z - r_{3}) (z - r_{4}), \end{matrix}

ahol

a

b

c

d

e

egész számok és

a \neq 0

. Bizonyítsuk be, hogy ha

r_{1} + r_{2}

racionális szám és

r_{1} + r_{2} \neq r_{3} + r_{4}

, akkor

r_{1} r_{2}

racionális szám.

B5. Legyenek

A

B

C

egymástól egyenlő távolságra lévő pontok egy

O

középpontú egységnyi sugarú körvonalon és legyen

P

tetszőleges pont a kör belsejében. Jelölje a

P

távolságát az

A

B

C

pontoktól rendre

a

b

és

c

. Bizonyítsuk be, hogy van olyan

a

b

c

oldalú háromszög, amelynek a területe csak az

O P

távolságtól függ.

B6. Legyen

f (x)

[0; 1]

intervallumon értelmezett folytonos valós értékű függvény. Bizonyítsuk be, hogy

\begin{matrix} \int_{0}^{1} \int_{0}^{1} | f (x) + f (y) | d x d y \geq \int_{0}^{1} | f (x) | d x . \end{matrix}