Cím: Geometriai terek az algebra szemszögéből
Szerző(k):  Schmidt Tamás 
Füzet: 2004/április, 199 - 206. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A geometriában pontokkal, egyenesekkel, síkokkal foglalkozunk, és a közöttük fennálló kapcsolatokat vizsgáljuk. Ehhez bizonyos alaptulajdonságokat ‐ ún. axiómákat ‐ kell rögzíteni. Ilyen pl. az, hogy bármely két, különböző ponton pontosan egy egyenes megy át vagy az, hogy két különböző egyenesnek legfeljebb egy közös pontja lehet. Többféle geometriai térfogalom ismeretes, ezeket axiómákkal adjuk meg. Most a projektív terek elemeivel itt ismerkedünk meg. Ezek közül is elsősorban az ún. véges projektív síkokról ejtünk néhány szót.
Mit értünk projektív sík alatt? Adva vannak a pontok, amelyek egy G halmazt alkotnak. Egy egyenest úgy tudunk megadni, hogy megmondjuk, a G mely pontjait tartalmazza. Egy egyenes tehát nem más, mint a G-nek egy részhalmaza. A projektív síkot tehát úgy tekinthetjük, hogy az egyrészt egy G halmazból, másrészt a G bizonyos kitüntetett részhalmazaiból ‐ az egyenesek összességéből ‐ áll, eleget téve a következő axiómáknak.

(P1)Két különböző ponthoz pontosan egy olyan egyenes van, amely mindkét pontot tartalmazza.
(P2)Két különböző egyenesnek pontosan egy közös pontja van.
(P3)Van négy pont, amelyek közül bárhogyan választunk is ki három pontot, azok nem fekszenek egy egyenesen.

 
 

1. ábra. A Fano sík
 

A (P3) axióma csak azért szükséges, hogy a triviális eseteket kizárjuk. A legkisebb elemszámú projektív síknak 7 pontja van, ez az ún. Fano sík, amelyet az 1. ábra szemléltet. Itt 7 pont van, amelyeket A,B,...,G jelöl. Az egyenesek pedig az ábrán látható hat egyenesre eső ponthármasok és a berajzolt körön levő három pont. (Tehát az egyenesek száma is 7.)
 
Síkok megadása koordináták segítségével
 

Hogyan lehet további példákat adni véges projektív síkra? Mielőtt erre választ adnánk, nézzük meg, hogy a ,,szokásos'' geometriai térben hogyan juthatunk a P(1), P(2), P(3) axiómáknak eleget tevő konfigurációhoz (amelynek az iménti példával szemben persze végtelen sok pontja és egyenese van). Az első ötlet az lehetne, hogy tekintsük egy S sík ,,közönséges'' pontjait és egyeneseit. A P(1) és a P(3) axióma nyilvánvalóan teljesül, a P(2) viszont nem, mivel a párhuzamos egyeneseknek nincs közös pontjuk. A projektív geometriában ezért a ,,közönséges'' pontokon és egyeneseken kívül ún. ideális pontokat és egyeneseket is bevezetünk; jelen esetben ezt a következőképpen tehetjük meg. Vegyünk fel a térben a szokásos módon egy derékszögű koordinátarendszert, és legyen a szóbanforgó S sík az (X,Y,1) koordinátájú pontok összessége, ahol X és Y tetszőleges valós számok lehetnek. Ekkor az S minden pontját egyértelműen jellemezhetjük azzal az egyenessel, amelyet ő és a koordinátarendszer origója határoz meg (ez az az origóból induló egyenes, amely az S-et a kiszemelt pontban döfi). Egy ilyen egyenest pedig az iránya határoz meg, vagyis egy nemnulla (A,B,C) vektor, ami az S síkkal nem párhuzamos. Nyilván az (A,B,C) és a (tA,tB,tC) vektorok az S sík ugyanazon pontját jelölik ki, ha t tetszőleges nemnulla szám. Az, hogy az (A,B,C) vektor nem párhuzamos S-sel azt jelenti, hogy C≠0. Definiáljuk ezután az S' projektív síkot úgy, hogy annak ,,pontjai'' a nem csupa nullából álló valós (A,B,C) számhármasok; két ilyen számhármast pontosan akkor tekintünk egyenlőnek, ha egymásnak nemnulla számszorosai. Látható, hogy ezzel az S' síknak legalább annyi pontja van, mint S-nek; a különbség azokból a számhármasokból adódik, amelyeknek harmadik eleme nulla (ezeket nevezzük ideális pontoknak).
Az S' pontjai után térjünk rá az egyenesek meghatározására. Induljunk ki az S sík ,,közönséges'' egyeneseiből. Egy ilyen egyenest egyértelműen jellemez egy olyan, az origón átmenő (az S-sel nem párhuzamos) sík, amely őt az S-ből kimetszi; egy ilyen sík pedig egyértelműen leírható a normálvektorával, azaz az origóban rá állított merőlegessel. Ez a merőleges egyenes pedig ismét egy nem csupa nullából álló számhármassal jellemezhető. Az a követelmény, hogy a sík metszi S-et a normálvektorára nézve azt jelenti, hogy az első két koordinátája közül valamelyik nem nulla. Ha a normálvektor az (a,b,c) számhármassal van megadva, akkor az egyenesnek azok az (X,Y,Z) számhármasok a pontjai, amelyeknek megfelelő vektorok merőlegesek a normálvektorra, azaz a vele képezett skalárszorzatuk nulla, vagyis amelyekre aX+bY+cZ=0. Ennek kiterjesztéseként a következőképpen adhatjuk meg az S' egyeneseit: tetszőleges, de nem csupa nullából álló (a,b,c) számhármasra alkossák a neki megfelelő egyenest azok a nem csupa nullából álló (X,Y,Z) számhármasok, amelyekre aX+bY+cZ=0 teljesül. (Ha a vagy b nem nulla, akkor közönséges, míg a=b=0 esetén ideális egyenesről beszélhetünk. Könnyen látható, hogy ideális egyenes minden pontja ideális pont.) Megmutatható (és később, általánosabb feltételek mellett meg is mutatjuk), hogy az S' pontjai és egyenesei kielégítik nem csak a P(1) és a P(3) axiómákat (ezeket újra meg kellene nézni, hiszen a pontok és az egyenesek halmaza is más, mint S esetében!), hanem a P(2) axiómát is.
 
Számok helyett: testek
 

Próbáljuk meg általánosítani az S' sík iménti konstrukcióját. Ehhez szükségünk lesz a test fogalmára.
 

(Kommutatív) testnek nevezünk egy K halmazt, ha abban értelmezve van két művelet, az összeadás és a szorzás, jelölésük a+b és a⋅b=ab, melyek a következő tulajdonságokkal rendelkeznek:

(1)Ha a és b a K elemei, úgy a+b és ab is a K elemei.
(2)a+b=b+a, a+(b+c)=(a+b)+c, ab=ba, a(bc)=(ab)c (ezeket úgy mondjuk, hogy az összeadás és a szorzás egyaránt kommutatív és asszociatív) és érvényes a disztributivitás: a(b+c)=ab+ac.
(3)K-ban van két kitüntetett elem, a 0 és az 1, amelyekre teljesülnek az 0+a=a, 1⋅a=a azonosságok.
(4)Az a+x=0 egyenlet minden a-ra megoldható, megoldása -a.
(5)Az ax=1 egyenlet minden a≠0-ra megoldható, megoldása a-1, vagy másképp jelölve 1a.

Testre példa a racionális vagy a valós számok teste, a szokásos összeadással és szorzással. Könnyen megadhatunk véges sok elemből álló testet is. Legyen p egy prímszám, és tekintsük a 0,1,2,...,p-1 számokat; ezek GF(p)-vel jelölt halmazán definiáljuk az összeadást és szorzást úgy, hogy elvégezzük a műveleteket az egész számok között, majd az eredményt p-vel maradékosan elosztjuk, és a maradék lesz az összeadás, illetve a szorzás eredménye. (Például GF(5)-ben 3+4=2, 3⋅3=4.) Megmutatható, hogy ezzel GF(p) valóban test, aminek p eleme van. Kimutatható (az előbbinél persze lényegesen bonyolultabban), hogy egy véges (sok elemből álló) testnek mindig pk számú eleme van, ahol p prím, és megfordítva: minden pk prímhatványhoz létezik, méghozzá bizonyos tekintetben egyértelműen egy pk darab elemből álló test (amelyet az előbbi jelölés mintájára GF(pk) jelöl).
 

Egy K test segítségével a következőképpen tudunk projektív síkot létrehozni. Képezzük K elemeivel az összes (X1,X2,X3) elemhármast, amelynek elemei nem mind egyenlők nullával; ezeket nevezzük pontoknak. Amennyiben λ a K test tetszőleges, 0-tól különböző eleme, akkor az (X1,X2,X3) és (λX1,λX2,λX3) számhármasokat ugyanazon pont előállításainak tekintjük. Az X1, X2, X3 számokat a pont projektív koordinátáinak hívjuk. Most áttérünk az egyenesek meghatározására. Legyenek a1, a2, a3 a K elemei, amelyek nem mind nullák. Az [a1,a2,a3] egyenes mindazon (X1,X2,X3) pontokat tartalmazza, amelyekre a1X1+a2X2+a3X3=0. Megmutatjuk, hogy az így definiált pontok és egyenesek projektív síkot alkotnak. Lássuk be először a (P1) axióma teljesülését. Legyen (A1,A2,A3) és (B1,B2,B3) két különböző pont. Az
x1A1+x2A2+x3A3=0,x1B1+x2B2+x3B3=0
egyenletrendszert kell megoldani az x1, x2, x3 ismeretlenekre. Feltehető, hogy például A1≠0; vonjuk ki az első egyenlet B1A1-szeresét a másodikból. Rendezés után kapjuk, hogy
x2(B2-A2⋅B1A1)+x3(B3-A3⋅B1A1)=0.
Mivel két különböző pontról van szó, azért
(B1,B2,B3)≠B1A1(A1,A2,A3)=(B1,A2⋅B1A1,A3⋅B1A1);
feltehető tehát, hogy például B2-A2⋅B1A1≠0, és így x2=x3A3B1-A1B3A1B2-A2B1, innen pedig például az első egyenletbe való behelyettesítés révén kapjuk, hogy x1=x3A2B3-A3B2A1B2-A2B1. Ezzel (A1≠0≠A1B2-A2B1 esetén)
=x3[A2B3-A3B2A1B2-A2B1,A3B1-A1B3A1B2-A2B1,1]==x3A1B2-A2B1[A2B3-A3B2,A3B1-A1B3,A1B2-A2B1],
azaz a keresett egyenes homogén koordinátái egyértelműen léteznek, és ezzel a (P1) axiómát igazoltuk. A (P2) belátásához tegyük fel, hogy [a1,a2,a3] és [b1,b2,b3] két különböző egyenes; közös (X1,X2,X3) pontjuk kereséséhez az
a1X1+a2X2+a3X3=0,b1X1+b2X2+b3X3=0
egyenletrendszert kell megoldani az X1, X2, X3 ismeretlenekre. Látható, hogy ez (alakjában és feltételeiben) lényegében ugyanaz az egyenletrendszer, mint az előbbi, így annak megoldása egyben a (P2) axiómát is bizonyítja. Végül a (P3) belátásához könnyen ellenőrizhető, hogy például az (1,0,0), (0,1,0), (0,0,1), (1,1,1) pontok közül semelyik három sincs egy egyenesen.
 

Nézzünk egy konkrét példát a leírt konstrukcióra. A legkisebb test kételemű, GF(2), amelynek elemei 0 és 1. E két szám segítségével készítsük el a következő hármasokat:
B=(1,0,0),F=(0,1,0),E=(0,0,1),D=(1,1,0),G=(1,0,1),A=(0,1,1),C=(1,1,1).


Könnyen belátható, hogy ez éppen a Fano sík. Tehát a Fano sík koordinátákkal is megadható; ezért azt mondjuk, hogy a Fano sík koordinátázható.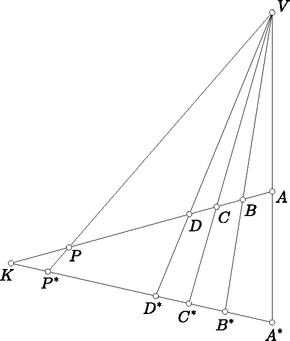
 
 

2. ábra. Két egyenes pontjainak egymáshoz rendelése
 

Alkalmazzuk ezután a konstrukciót egy tetszőleges véges, q=pk elemű testre, ahol p prímszám. A pontok számát a következőképpen kaphatjuk meg: nem csupa nulla ,,szám''hármasból q3-1 darab van, ezek mindegyikének q-1 darab nemnulla számszorosa lévén, (q-1)-esével adják ugyanazt a pontot, amelyek száma ezért q3-1q-1=q2+q+1. Hasonlóan kapjuk, hogy az egyenesek száma is q2+q+1. Nem nehéz megmutatni, hogy ez nem csak a koordinátázható síkok esetében van így, hanem minden véges projektív síknál ez a helyzet: a pontok és az egyenesek száma mindig egyenlő és q2+q+1 alakú, alkalmas q-val. A 2. ábráról könnyen leolvasható ugyanis, hogy a sík bármely két egyenesén a pontok száma ugyanannyi, hiszen pontjaik egy külső V pontból húzott szelők segítségével kölcsönösen egyértelműen megfeleltethetők egymásnak; ezt a számot (q+1)-gyel jelölhetjük. Ennek segítségével bizonyítható, hogy minden pont q+1 egyenesre illeszkedik (l. 3. ábra). Ezután pedig ‐ a sík pontjait egy adott ponton átmenő összes egyenes pontjaiként leszámlálva ‐ kapjuk, hogy a sík pontjainak száma 1+(q+1)q=q2+q+1. A véges matematika mindmáig híres megválaszolatlan kérdése, hogy ‐ nem koordinátázható síkok esetében ‐ ez a q szám lehet-e más, mint prímhatvány.
 
 

3. ábra. Egy pontra illeszkedő egyenesek és egy másik egyenesre illeszkedő pontok egymáshoz rendelhetők
 

 
A Desargues-tétel
 

Természetesen adódik a kérdés, hogy vajon minden véges projektív sík koordinátázható-e egy véges test segítségével? A válasz nemleges, de hogy melyek koordinátázhatók, arra igen szép és meglepő feltétel adható. Az elemi geometriai tételek hosszú sorában szerepel egy híres tétel, a Desargues-tétel, ami a következőképpen szól: ha a projektív sík Ai, Bi, Ci pontjai által meghatározott A1A2, B1B2, C1C2 egyenesek egy közös O ponton mennek át, akkor az A1B1, A2B2 egyenesek metszéspontját C3-mal, az A1C1, A2C2 egyenesek metszéspontját B3-mal, a B1C1, B2C2 egyenesek metszéspontját A3-mal jelölve, az A3, B3, C3 pontok egy egyenesen fekszenek. Viszonylag könnyű igazolni, hogy minden koordinátázható projektív síkban teljesül a Desargues-tétel.
Annál meglepőbb viszont, hogy ennek az állításnak igaz a megfordítása: ha egy projektív síkban igaz a Desargues-tétel, akkor a sík koordinátázható. Ezzel a Desargues-tétel fontos szerephez jutott, ő a felelős a sík koordinátázhatóságért.
A projektív sík kétdimenziós. Hogyan lehet magasabb dimenziós projektív tereket definiálni? A (P1) axióma változatlan, viszont (P2)-t módosítani kell, hiszen létezik két olyan egyenes, amelyeknek nincs közös pontja (kitérő egyenesek). Két egyenesnek pontosan akkor van közös pontja, ha egy síkban vannak. Ezt fogalmazza meg a
 

(P 02) Pasch axióma. Ha egy nem elfajuló háromszög két oldalegyenesét egy további egyenes a háromszög csúcspontjaitól különböző pontokban metszi, akkor ez az egyenes a háromszög harmadik oldalegyenését is metszi. Magasabb dimenziós projektív tereket a síkokhoz hasonló módon állíthatunk elő egy test segítségével. Az n>2 dimenziós teret úgy kapjuk, hogy hármasok helyett elem (n+1)-eseket tekintünk. Meglepő, hogy a 3 és annál magasabb dimenziós projektív terekben mindig teljesül a Desargues-tétel, ezért koordinátázhatók. Ez egyben azt is jelenti, hogy egy olyan projektív sík, amelyben nem teljesül a Desargues-tétel nem lehet benne egy magasabb dimenziójú projektív térben.
 

Vázoljuk ennek a bizonyítását a következő formában: ha az S projektív sík része egy 3-dimenziós projektív térnek, akkor igaz benne a Desargues-tétel (l. 5. ábra). A bizonyításnak az az ötlete, hogy az A2B2C2 háromszöget az S síkból ,,kihúzzuk a térbe''. Ez azt jelenti, hogy olyan A*, B*, C* pontokat keresünk az S-en kívül, amelyeknek egy O'-ből az S-re való vetülete rendre A2, B2 és C2, és amelyekre teljesül, hogy az A1A*, B1B*, C1C* egyenesek egy közös O* ponton mennek keresztül. Jelölje az A1B1 és A*B* egyenesek metszéspontját C33, az A1C1 és A*C* egyenesek metszéspontját B33, a B1C1 és B*C* egyenesek metszéspontját pedig A33. Ekkor ezek a pontok egyrészt S-en vannak, hiszen az ottani A1B1, A1C1, B1C1 egyeneseken fekszenek, másrészt ugyanilyen okból az S síkon kívüli A*B*C* háromszög síkjában is benne vannak. Így ez a három pont két sík közös részéhez tartozván egy egyenesbe esik. Másrészt ezeknek a pontoknak O'-ből az S-re eső vetületei éppen A3, B3 és C3, hiszen pl. A*B* vetülete A2B2 lévén az A*B* és az S-ben levő A1B1 egyenes metszéspontjának vetülete csak A2B2 és A1B1 metszéspontja, azaz C3 lehet; tehát C33 vetülete C3, ezért C33=C3, és ugyanígy B33=B3 és A33=A3. Így A3, B3 és C3 valóban egy egyenesbe esik.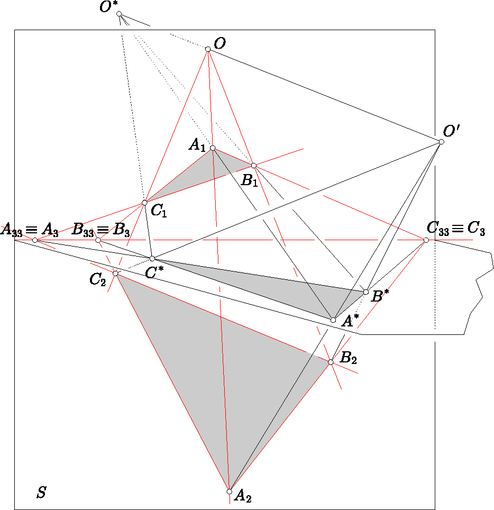
 
 

5. ábra. A Desargues-tétel ,,térbeli'' bizonyítása
 

Meg kell még mutatni, hogy az A*, B*, C* pontok megválaszthatók a kívánt módon. Ehhez vegyünk fel az S síkon kívül tetszőlegesen egy O* pontot úgy, hogy annak az S-re eső vetülete éppen az A1A2, B1B2, C1C2 egyenesek közös pontja, O legyen. Ezután például az A* pontot úgy kaphatjuk, hogy az A1O* egyenest metsszük azzal a vetítés irányába eső egyenessel, amely átmegy az A2 ponton. (A metszéspont létezik, hiszen mindkét egyenes az A1OO* háromszög síkjában halad.)
 
Kitekintés a fizikára és azon is túlra...
 

A geometriai tereket többek között az jellemzi, hogy az ,,altereik'' között milyen tartalmazási viszonyok érvényesek. Az alterek (mint a ,,közönséges'' térben a pontok, egyenesek, síkok, ill. maga az egész tér) a pontok G halmazának bizonyos részhalmazai, és így a halmazelméleti tartalmazás egy rendezést határoz meg körükben. Két altér közös része (metszete) ismét altér, amely az adott két altér legnagyobb alsó korlátja. Két altér halmazelméleti egyesítése általában nem altér, de létezik egy legszűkebb altér, amely őket tartalmazza. Ez a két altér legkisebb felső korlátja. Ez azt jelenti, hogy az alterek részben rendezett halmaza olyan, hogy ott bármely két elemnek létezik legkisebb közös felső és legnagyobb közös alsó korlátja. Az ilyen részben rendezett halmazt hálónak nevezzük. Mivel a legkisebb felső és legnagyobb alsó korlát egyértelműen meghatározott, a képzésüket algebrai műveleteknek tekinthetjük, elnevezésük egyesítés, ill. metszet. A háló tehát egy speciális algebrai struktúra, amelyet a geometriai térhez rendelhetünk, és ami jellemzi a teret.
A huszadik század elején a fizikában két elmélet állt az érdeklődés középpontjában. Az egyik az Einstein-féle relativitáselmélet, a másik a kvantummechanika. Az utóbbi matematikai modelljét kísérelték meg leírni, amikor a 30-as években Neumann János bekapcsolódott e munkába. Mint a matematika megannyi területén, itt is sikerült igen jelentőset alkotnia. A kvantummechanika matematikai modelljének megadásához a projektív geometriai tereknek egy általánosítását adta, amelyet folytonos geometriának nevezett. Ennek egyik érdekessége, hogy nincsenek benne pontok, minden altér tartalmaz egy másik alteret. Míg a projektív geometriánál az alterek dimenziója az 1,2,...,n természetes számok valamelyike, addig a folytonos geometriánál az altér dimenziója egy tetszőleges 0 és 1 közötti valós szám lehet, ez a tulajdonság utal az elnevezésben szereplő folytonosságra. Neumann bebizonyította, hogy ezek is koordinátázhatók, de nem testekkel, hanem általánosabb struktúrákkal, ún. gyűrűkkel. Ezek annyiban különböznek a testektől, hogy az 1 elem létezését és a (5) tulajdonság teljesülését nem követeljük meg.