Kezdőlap


Cím:	Egy fizika feladat megoldása "a Könyvből"
Szerző(k):	Gnädig Péter
Füzet:	2004/december, 559 - 564. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Erdős Pál (1913‐1996), a világhírú magyar matematikus gyakran emlegette, hogy a Jóistennek (aki természetesen matematikus) van egy Könyve, amelyben a matematikai tételek tökéletes megoldását őrzi. A matematikusok, amikor rácsodálkoznak egy probléma nagyon egyszerű és emiatt különösen szép, frappáns megoldására, akkor azt mondják: Ez a Könyvből való bizonyítás! Erdős véleménye szerint egy matematikusnak nem kell hinnie Istenben, de hinnie kell a Könyvben¹!
A fizikusok közül sokan úgy vélik, hogy a Könyv nem csupán matematikai tételek bizonyításával van tele, jut benne hely a fizika (és más tudományágak) problémáinak is. Ha ez így van, akkor az alábbi feladat és annak megoldása sem hiányozhat közülük!

*

A probléma. Egy

h

magas toronyból adott

v_{0}

nagyságú kezdősebességgel különböző irányokba hajíthatunk el pontszerű testeket. Legfeljebb mekkora (vízszintesen mért) távolságra juthatnak el a testek, ha a légellenállás nem számottevő?

Ez a feladat (amely sokféleképpen, pl. egy

h

magas súlylökő leghatékonyabb dobóstratégiájának megkereséseként is megfogalmazható) többféle módon is megoldható. Az alábbiakban négy megoldást is bemutatunk, ezek közül az első bizonyára nem nyerné el a szépségdíjat. (Akik még nem ,,barátkoztak meg'' a differenciálszámítással, nyugodtan átugorhatják a megoldás (5) egyenlet utáni részét, legfeljebb annak hosszára vessenek egy pillantást!) A másodikról a jelen sorok írója sokáig azt hitte, hogy a Könyvből való, mindaddig, amíg meg nem ismerkedett a harmadik megoldással. Ennek megértéséhez azonban egy olyan matematikai művelet ismerete szükséges, amellyel esetleg nem minden középiskolás találkozott, ezért megadunk egy negyedik, csak elemi geometriai és fizikai ismereteket igénylő megoldási módot is. A harmadik és a negyedik megoldás lényegében egyenértékű, csak megfogalmazásuk különböző. Olvasóink eldönthetik, hogy véleményük szerint vajon melyik kerülhet be a Könyvbe.
Mielőtt belekezdenénk a részletes megoldásba, bevezetünk egy hasznos jelölést:

v_{0}

-t

\sqrt[]{2 g H}

alakban írjuk fel, ahol

H

egy hosszúság dimenziójú állandó.

H

szemléletes jelentése: ilyen magasról leejtett test éppen a feladatban szereplő

v_{0}

sebességgel érne földet. A továbbiakban a hajítások kezdősebességét mindig átszámítjuk

H

-ra, és a maximális dobási távolságot is

H

egységekben fogjuk kifejezni.

I. megoldás. Írjuk le a test mozgását, vagyis a ferde hajítás folyamatát az 1. ábrán látható derékszögű koordináta-rendszerben!

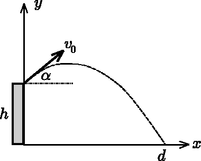1. ábra

A vízszintes (

x

tengely irányú) mozgás egyenletes:

\begin{matrix} x (t) = v_{0} \cdot cos α \cdot t, \end{matrix}

(1)

ahol

α

az elhajítás irányának a vízszintessel bezárt szöge.
A függőleges, egyenletesen gyorsuló mozgást leíró összefüggés:

\begin{matrix} y (t) = - \frac{g}{2} t^{2} + v_{0} \cdot sin α \cdot t + h . \end{matrix}

(2)

Az (1) egyenletből kifejezhetjük az időt:

\begin{matrix} t = \frac{x}{v_{0} cos α}, \end{matrix}

majd ezt (2)-be helyettesítve megkapjuk a pályagörbe egyenletét:

\begin{matrix} y = - \frac{g}{2 v_{0}^{2} cos^{2} α} x^{2} + x tg α + h . \end{matrix}

(3)

A hajítás vízszintes távolságát,

d

-t úgy kapjuk meg, hogy a fenti egyenletben

y

helyébe 0-t írunk (hiszen a földet érésre ez jellemző), s a hozzá tartozó

x

éppen a szóban forgó

d

lesz. Tehát

\begin{matrix} 0 = - \frac{g}{2 v_{0}^{2} cos^{2} α} d^{2} + d tg α + h, \end{matrix}

(4)

ami a korábban említett

v_{0} = \sqrt[]{2 g H}

jelöléssel

\begin{matrix} 0 = - \frac{d^{2}}{4 H cos^{2} α} + d tg α + h \end{matrix}

(5)

alakra hozható. Ez

d

-re nézve egy másodfokú egyenlet, melynek számunkra érdekes (

d > 0

) megoldása:

\begin{matrix} d (α) = 2 H [sin α cos α + \sqrt[]{{(sin α cos α)}^{2} + \frac{h}{H} cos^{2} α}] . \end{matrix}

(6)

A szélsőértékszámítás szabályai szerint ennek a kifejezésnek

d' (α)

deriváltja a maximális

d

értéknél nulla. Ez a feltétel megadja a kérdéses

α

szöget, ahonnan (meglehetősen bonyolult számolás után)

d_{{max}_{}^{}}

is meghatározható. Egyszerűbben célhoz érünk, ha képezzük az (5) egyenlet

α

szerinti deriváltját, miközben kihasználjuk, hogy a keresett helyen

d' (α) = 0,

vagyis

d

állandónak tekinthető:

\begin{matrix} \frac{d}{d α} [- \frac{d^{2}}{4 H cos^{2} α} + d tg α + h] = - \frac{d^{2}}{4 H} \frac{2 sin α}{cos^{3} α} + \frac{d}{cos^{2} α} = 0, \end{matrix}

(7)

azaz

\begin{matrix} d = \frac{2 H}{tg α} . \end{matrix}

Ezt (5)-be helyettesítve és a kapott egyenletet

tg α

-ra megoldva

\begin{matrix} tg α = \sqrt[]{\frac{H}{H + h}}; \end{matrix}

(8)

a legnagyobb hajítási távolságra pedig

\begin{matrix} d_{{max}_{}^{}} = 2 H \sqrt[]{\frac{H + h}{H}} = \frac{v_{0}}{g} \sqrt[]{v_{0}^{2} + 2 g h} \end{matrix}

(9)

adódik.

Megjegyzés: A talajszintről (

h = 0

) történő hajításnál visszakapjuk a jól ismert

α = 45^{\circ}

és

d_{{max}_{}^{}} = 2 H = v_{0}^{2} / g

összefüggéseket.

II. megoldás. A feladat elemi matematikával, differenciálszámítás alkalmazása nélkül is megoldható. Induljunk ki az (5) egyenletből, és használjuk ki az

\frac{1}{cos^{2} α} = 1 + tg^{2} α

trigonometrikus azonosságot! Ekkor az

u = tg α

jelöléssel a következő egyenletet kapjuk:

(1 + u^{2}) d^{2} - 4 u d H - 4 h H = 0

. Ez az egyenlet nemcsak

d

-re nézve másodfokú, hanem (adott

d

esetén) az

u

változóban is másodfokú egyenlet:

\begin{matrix} u^{2} \cdot d^{2} - u \cdot 4 d H + (d^{2} - 4 h H) = 0. \end{matrix}

Ennek akkor van valós megoldása, ha a diszkriminánsa nem negatív, azaz

\begin{matrix} {(2 d H)}^{2} - d^{2} (d^{2} - 4 h H) \geq 0. \end{matrix}

Innen

\begin{matrix} d^{2} \leq 4 H^{2} + 4 h H \end{matrix}

adódik, és a határeset (az egyenlőség) nyilván a legnagyobb hajítási távolságnak felel meg; ez pedig éppen (9)-cel egyenértékű.

III. megoldás. Jelöljük a kezdősebesség vektorát

v_{0}

-lal, a földet érés sebességét

v_{1}

-gyel, a teljes mozgáshoz tartozó elmozdulásvektort

r

-rel, a nehézségi gyorsulást (mint vektort) pedig

g

-vel (2. ábra)!

2. ábra

Newton II. törvénye szerint

\begin{matrix} \frac{v_{1} - v_{0}}{t} = g, \end{matrix}

(10)

ahol

t

a mozgás időtartama. (Kihasználtuk, hogy a gyorsulás időben állandó, ezért a pillanatnyi gyorsulás és az átlagos gyorsulás megegyezik.)
Másrészt igaz, hogy

\begin{matrix} \frac{v_{1} + v_{0}}{2} \cdot t = r, \end{matrix}

(11)

itt azt használtuk ki, hogy a sebesség időben egyenletesen változik, tehát az átlagsebesség megegyezik a kezdeti- és végsebesség számtani közepével.
Szorozzuk össze a fenti két vektor-egyenletet skaláris szorzással:

\begin{matrix} \frac{v_{1}^{2} - v_{0}^{2}}{2} = gr = g h, \end{matrix}

azaz a földetérés sebességének nagysága

\begin{matrix} v_{1} = \sqrt[]{v_{0}^{2} + 2 g h} . \end{matrix}

Ez nem túl érdekes összefüggés, hiszen az energiamegmaradás törvényéből ezt már korábban is tudtuk. Meglepő eredményt kapunk azonban akkor, ha a (10) és (11) egyenleteket vektoriális szorzással szorozzuk össze. Felhasználva, hogy

v_{0} \times v_{1} = - v_{1} \times v_{0}

, továbbá

v_{0} \times v_{0} = v_{1} \times v_{1} = 0

, azt kapjuk, hogy

\begin{matrix} v_{1} \times v_{0} = g \times r . \end{matrix}

Képezzük a fenti egyenlet mindkét oldalának abszolút értékét (és használjuk fel, hogy két vektor vektoriális szorzatának nagysága a tényezők abszolút értékeinek és a közbezárt szög szinuszának a szorzata):

\begin{matrix} | v_{1} \times v_{0} | = | v_{0} | | v_{1} | sin γ = v_{0} \sqrt[]{v_{0}^{2} + 2 g h} \cdot sin γ = | g \times r | = g \cdot d . \end{matrix}

(12)

(Kihasználtuk, hogy

g

és

r

vektoriális szorzásánál

r

-nek csak a vízszintes komponense számít, ennek hossza pedig éppen a keresett vízszintes elmozdulás.)
A (12) egyenletből leolvasható, hogy

d

akkor a legnagyobb, amikor a

v_{0}

és a

v_{1}

vektorok merőlegesek egymásra, és a legnagyobb hajítási távolság

\begin{matrix} d_{{max}_{}^{}} = \frac{v_{0}}{g} \sqrt[]{v_{0}^{2} + 2 g h}, \end{matrix}

összhangban (9)-cel.
Ha a kezdősebesség vízszintessel bezárt szögét a korábbiaknak megfelelően

α

-val jelöljük, akkor a sebesség vízszintes komponensének állandóságából, valamint a kezdő- és végsebesség merőlegességéből

v_{0} \cdot cos α = v_{1} \cdot cos (90^{\circ} - α) = v_{1} \cdot sin α

, azaz

\begin{matrix} tg α = \frac{v_{0}}{v_{1}} = \frac{v_{0}}{\sqrt[]{v_{0}^{2} + 2 g h}} \end{matrix}

adódik, ami (8)-cal egyenértékű.

IV. megoldás. Kövessük a III. megoldás gondolatmenetének elejét, írjuk fel a (10) és (11) egyenleteket, majd tekintsük a kezdeti- és a végsebesség vektora által kifeszített

O B C A

paralelogrammát (3. ábra)!

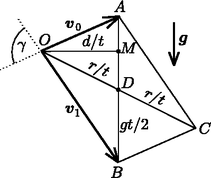3. ábra

Számítsuk ki a paralelogramma

T

területét kétféle módon. Egyrészt

T = | v_{0} | | v_{1} | sin γ

, másrészt

\begin{matrix} T = A B \cdot O M = g t \cdot \frac{d}{t} = g d . \end{matrix}

Kihasználtuk, hogy az

A B

szakasz függőleges és (10) szerint

g t

hosszúságú, valamint (11) alapján

O D

hossza

r / t

, tehát

O D

vízszintes (

A B

-re merőleges) vetülete

O M = d / t

. A kétféle számítás eredményét összehasonlítva kapjuk, hogy

\begin{matrix} d = \frac{1}{g} | v_{0} | | v_{1} | sin γ \leq \frac{1}{g} v_{0} \sqrt[]{v_{0}^{2} + 2 g h} = d_{{max}_{}^{}} . \end{matrix}

Látható az is, hogy az egyenlőség akkor teljesül, amikor a kezdeti- és a végsebesség merőleges egymásra, továbbá az elhajítás

α

szögére ilyenkor (az

O M A

és

B O A

derékszögű háromszögek hasonlósága miatt) fennáll:

\begin{matrix} tg α = \frac{A M}{O M} = \frac{A O}{O B} = \frac{v_{0}}{v_{1}} = \frac{v_{0}}{\sqrt[]{v_{0}^{2} + 2 g h}} . \end{matrix}

Valamennyi eredményünk érvényben marad akkor is, ha

h < 0

(de természetesen

v_{0}^{2} > 2 g | h |

). Ilyenkor a feladat egyik lehetséges megfogalmazása így hangzik:

Egy adott mélységű gödörből földet lapátolunk ki. Milyen irányban dobjuk el a kiásott földet, ha azt akarjuk elérni, hogy a lehető legmesszebb érje el a külső talajszintet, és mekkora ez a ,,legmesszebb''?

Itt is és a súlylökő esetében is feltételezzük, hogy a föld eldobásának, illetve a súly ellökésének kezdősebessége független a dobás irányától. Ezen feltevések jogosságának igazolása vagy frappáns cáfolata azonban már a Könyv biofizika fejezetében keresendő!

¹Idén jelent meg a Typotex kiadó gondozásában M. Aigner ‐ G. M. Ziegleg: Bizonyítások a Könyvből című munkája, amely több mint száz matematikai probléma ilyen szellemű megoldását tartalmazza.