Kezdőlap


Cím:	35. Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):	Honyek Gyula , Tasnádi Tamás
Füzet:	2004/november, 491 - 501. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Elméleti feladatok megoldása¹

1. feladat. ,,Pingpong-ellenállás''

(a)

R

sugarú, egymástól

d

(

d ≪ R

) távolságra levő kondenzátorlemezek között ható elektrosztatikus erőt két lényegesen különböző módon is kiszámolhatjuk a kondenzátorra kapcsolt

V

feszültség ismeretében:

i)

Az egyik, például az alsó lemezre ható erő megegyezik a lemezen tárolt

Q

töltésnek és a másik, felső lemez által keltett

E'

elektromos térerősségnek a szorzatával. A kondenzátoron belüli térerősség

E = \frac{V}{d} = 2 E'

, hiszen mindkét kondenzátorlemez azonos

E'

járulékot ad belül a térhez. Az egyes kondenzátorlemezek

Q

töltése a kondenzátorlemezt körülvevő hengerfelületre felírt Gauss-tételből kapható meg:

Q = 2 E' ε_{0} R^{2} π

. Ezek alapján az alsó lemezre ható elektrosztatikus vonzóerő:

\begin{matrix} F = ε_{0} \frac{V^{2} R^{2} π}{2 d^{2}} . \end{matrix}

(1)

i i)

A lemezek között ható erőt megkaphatjuk energetikai megfontolások segítségével is! Tegyük föl, hogy a lemezeket a köztük ható

F

erő ellenében kicsiny

Δ d

távolsággal eltávolítjuk egymástól. Minthogy a kondenzátor állandó

V

feszültségre van kapcsolva, és

C = ε_{0} \frac{R^{2} π}{d}

kapacitása megváltozik, töltése is megváltozik, mégpedig

\begin{matrix} Δ Q = V (C_{2} - C_{1}) = ε_{0} V R^{2} π (\frac{1}{d + Δ d} - \frac{1}{d}) \approx - ε_{0} V R^{2} π \frac{Δ d}{d^{2}} \end{matrix}

(2)

értékkel. (A negatív előjel töltéscsökkenést jelez. A közelítésnél felhasználtuk, hogy

{(1 + α)}^{- 1} \approx 1 - α

, ha

| α | ≪ 1

.)
A kondenzátorlemezek eltávolításakor végzett kicsiny

Δ W = F \cdot Δ d

munka kétféle energiaváltozást fedez. Egyrészt a kondenzátor energiája

Δ E_{kond} = \frac{1}{2} V \cdot Δ Q

értékkel változik meg, hiszen változik a rajta tárolt töltés. Másrészt a telep energiája

Δ E_{telep} = - V \cdot Δ Q

értékkel változik meg, hiszen az egymáshoz képest

V

potenciálkülönbségű kapcsok között

Δ Q

töltés vándorol át. (Ha

Δ Q > 0

, azaz a telep tölti a kondenzátort, akkor energiája csökken, ez indokolja a negatív előjelet.) Tehát a folyamatra a következő formában írható föl az energiamegmaradás tétele:

\begin{matrix} Δ W = F \cdot Δ d = Δ E_{kond} + Δ E_{telep} = - \frac{1}{2} V \cdot Δ Q = ε_{0} V^{2} R^{2} π \frac{Δ d}{2 d^{2}}, \end{matrix}

(3)

ahonnan közvetlenül adódik az előző pontban kapott (1) eredmény.
Felhívjuk a figyelmet arra az érdekes tényre, hogy annak ellenére, hogy a kondenzátorlemezek távolításakor munkát végeztünk, a kondenzátor energiája csökkent, mégpedig pontosan a végzett munkával megegyező értékkel,

Δ W = - Δ E_{kond}

. Ezzel szemben a telep energiája

Δ E_{telep} = 2 Δ W

értékkel nőtt, hiszen a kondenzátor ,,töltötte'' a telepet.

(b)

A kondenzátor alsó fegyverzetén fekvő

r

sugarú kis korong

q

töltése például a Gauss-tétel segítségével kapható meg. Írjuk föl a tételt egy olyan hengerfelületre, amely körbeveszi a kis korongot:

q = ε_{0} E r^{2} π = ε_{0} \frac{r^{2} π}{d} V

, ahonnan a keresett paraméter:

\begin{matrix} χ = ε_{0} \frac{r^{2} π}{d} . \end{matrix}

(4)

Kicsit szellemesebben, egyszerűbben is megkaphatjuk a keresett töltést, ha észrevesszük, hogy a fegyverzet teljes

Q

töltésének éppen a kis korong területére eső

\frac{r^{2}}{R^{2}}

hányada adja meg

q

-t.

(c)

A kis korong akkor emelkedik föl a fegyverzetről, ha a rá ható

q E'

elektrosztatikus erő megegyezik, vagy nagyobb, mint a lefelé mutató

m g

nehézségi erő. Hangsúlyozzuk, hogy az alsó fegyverzeten fekvő korongra ható elektrosztatikus erőt csupán a felső fegyverzet által keltett

E' = \frac{E}{2} = \frac{V}{2 d}

térből kell kiszámolnunk, hiszen az alsó fegyverzet nem fejt ki (függőleges irányú) elektrosztatikus erőt a kis korongra. Így a

V_{k}

küszöbfeszültségre az

m g = q E' = \frac{χ V_{k}^{2}}{2 d}

egyenletből a

\begin{matrix} V_{k} = \sqrt[]{\frac{2 m g d}{χ}} \end{matrix}

(5)

érték adódik.

(d)

Kövessük nyomon a kis korong mozgását, sebességének változását mozgásának egy periódusa alatt! Jelölje a korong sebességének nagyságát az alsó (1), ill. felső (2) fegyverzetnél közvetlenül az ütközés előtt (e) és után (u) rendre

v_{1e}

és

v_{1u}

, ill.

v_{2e}

és

v_{2u}

Az ütközési szám definíciója szerint

\begin{matrix} v_{1u} = η v_{1e}, v_{2u} = η v_{2e} . \end{matrix}

(6)

A két ütközés közti felfelé, illetve lefelé való mozgásra felírhatjuk a mechanikai energiamegmaradás tételét. A nehézségi erő munkájából adódó potenciális energiaváltozás

\pm m g d

, míg az elektromos tér munkája

q V = χ V^{2}

. Felhívjuk a figyelmet arra, hogy a nehézségi erő munkája negatív a fölfelé történő mozgásnál, és pozitív a lefelé való mozgásnál. Ezzel szemben a Coulomb-erő munkája mindkét esetben pozitív, hiszen az alsó fegyverzeten

q

töltésűre feltöltött korong a felső fegyverzeten leadja töltését, és

- q

töltésű lesz. Ezek figyelembevételével a mozgás két szakaszára a mechanikai energiamegmaradás törvénye

\begin{matrix} \begin{matrix} fel: \end{matrix} \frac{1}{2} m v_{2e}^{2} & = \frac{1}{2} m v_{1u}^{2} + χ V^{2} - m g d, & (7) \\ \begin{matrix} le: \end{matrix} \frac{1}{2} m v_{1e}^{2} & = \frac{1}{2} m v_{2u}^{2} + χ V^{2} + m g d & (8) \end{matrix}

alakban írható. A (6)‐(8) egyenletek felhasználásával rendre kifejezhetjük a

v_{2e}

v_{2u}

és

v_{1e}

sebességeket a

v_{1u}

sebességgel:

\begin{matrix} v_{2e}^{2} & = v_{1u}^{2} + \frac{2 χ V^{2}}{m} - 2 g d, & (9) \\ v_{2u}^{2} & = η^{2} v_{2e}^{2} = η^{2} (v_{1u}^{2} + \frac{2 χ V^{2}}{m} - 2 g d), & (10) \\ v_{1e}^{2} & = v_{2u}^{2} + \frac{2 χ V^{2}}{m} + 2 g d = η^{2} v_{1u}^{2} + (1 + η^{2}) \frac{2 χ V^{2}}{m} + (1 - η^{2}) 2 g d . & (11) \end{matrix}

Végül felhasználva (6) első egyenletét, valamint az utolsó, (11) összefüggést, az állandósult mozgás

v_{1u} = v_{s}

sebességére a következő egyenletet kapjuk:

\begin{matrix} (1 - η^{4}) v_{s}^{2} = η^{2} ((1 + η^{2}) \frac{2 χ V^{2}}{m} + (1 - η^{2}) 2 g d) . \end{matrix}

(12)

Az egyenlet megoldása

\begin{matrix} v_{s}^{2} = \frac{2 χ η^{2}}{m (1 - η^{2})} V^{2} + \frac{2 g d η^{2}}{1 + η^{2}}, \end{matrix}

(13)

ahonnan a keresett

α

és

β

együttható értéke:

\begin{matrix} α = \frac{2 χ η^{2}}{m (1 - η^{2})} és β = \frac{2 g d η^{2}}{1 + η^{2}} . \end{matrix}

(14)

(e)

Ha teljesül a

q V ≫ m g d

feltétel, akkor a kondenzátorlemezek között mozgó korongra ható elektrosztatikus erő jóval nagyobb, mint a nehézségi erő, így ez utóbbit elhanyagoljuk. Ekkor a korong mozgása szimmetrikus; az emelkedés és a süllyedés is egyenletesen gyorsuló mozgás, és a két mozgás csak irányában különbözik. Az előző pontban a sebességekre kapott kifejezések egyszerűsödnek, a (13), (9) és (6) formulák és

g = 0

felhasználásával azt kapjuk, hogy

\begin{matrix} v_{1u} = v_{2u} = \sqrt[]{α} V, v_{1e} = v_{2e} = \frac{1}{η} v_{1u} = \frac{\sqrt[]{α}}{η} V . \end{matrix}

(15)

A kis korong mozgásának egyik ‐ például az emelkedési ‐ félperiódusában

d

utat tesz meg egyenletesen gyorsulva

v_{1u}

-ról

v_{2e}

sebességre, így a félperiódus ideje

\begin{matrix} t = \frac{2 d}{v_{1u} + v_{2e}} = \frac{2 d η}{\sqrt[]{α} (1 + η) V} . \end{matrix}

Az átszállított töltés

q = χ V

, tehát az állandósult állapot elérése után a kis korong által szállított áram átlagos értéke

I = \frac{q}{t}

, ahonnan a keresett

γ

együttható:

\begin{matrix} γ = \frac{χ \sqrt[]{α} (1 + η)}{2 d η} = \sqrt[]{\frac{χ^{3} (1 + η)}{2 m d^{2} (1 - η)}} . \end{matrix}

(16)

(f)

Ebben a részfeladatban újra figyelembe kell vennünk a nehézségi erő hatását, hiszen kis feszültségértékeknél

q V / ≫ m g d

. A feszültséget csökkentve az áram akkor szűnik meg, amikor a korong sebessége olyan kicsinnyé válik, hogy az már nem emelkedik fel a felső fegyverzetig. A

V_{c}

kritikus feszültség mellett a korong éppen

v_{2e} = 0

sebességgel éri el a felső lapot. A (9) és (13) összefüggéseket felhasználva a

\begin{matrix} 0 = \frac{2 χ η^{2}}{m (1 - η^{2})} V_{c}^{2} + \frac{2 g d η^{2}}{1 + η^{2}} + \frac{2 χ}{m} V_{c}^{2} - 2 g d \end{matrix}

(17)

egyenletet kapjuk a kritikus feszültségre, melynek megoldása:

\begin{matrix} V_{c} = \sqrt[]{\frac{m g d (1 - η^{2})}{χ (1 + η^{2})}} = V_{k} \sqrt[]{\frac{1 - η^{2}}{2 (1 + η^{2})}} . \end{matrix}

(18)

I_{c}

kritikus áram mellett a kis korong éppen eléri a felső fegyverzetet, azaz

v_{2e} = v_{2u} = 0

, és lezajlik a töltéscsere ‐ hiszen folyik áram ‐, tehát a korongra ható Coulomb-erő iránya, és így az eredő erő nagysága is megváltozik a felső holtponton. A kritikus áram mellett (18) és (13) felhasználásával a

v_{1u}

és

v_{1e}

sebességekre azt kapjuk, hogy

\begin{matrix} v_{1 u, c} = 2 η \sqrt[]{\frac{g d}{1 + η^{2}}}, v_{1 e, c} = \frac{v_{1 u, c}}{η} = 2 \sqrt[]{\frac{g d}{1 + η^{2}}} . \end{matrix}

(19)

A korong nulla vég-, ill. kezdősebességű egyenletesen lassuló, ill. gyorsuló mozgást végez az emelkedési, ill. süllyedési szakaszon, azonban e két mozgás időtartama nem azonos. A (19) sebességek ismeretében az emelkedés, ill. süllyedés időtartama

\begin{matrix} t_{↑} = \frac{2 d}{v_{1 u, c}} = \frac{1}{η} \sqrt[]{\frac{d (1 + η^{2})}{g}}, t_{↓} = \frac{2 d}{v_{1 e, c}} = \sqrt[]{\frac{d (1 + η^{2})}{g}}, \end{matrix}

(20)

és egy teljes periódus alatt átszállított töltés

2 χ V_{c}

, tehát a kritikus áram:

\begin{matrix} I_{c} = \frac{2 χ V_{c}}{t_{↑} + t_{↓}} = \frac{2 η g}{1 + η^{2}} \sqrt[]{m χ \frac{1 - η}{1 + η}} . \end{matrix}

(21)

Minthogy

0 < η < 1

, a (18) egyenletből látszik, hogy a stacionárius mozgás fenntartásához szükséges

V_{c}

feszültség kisebb, mint a korong felemeléséhez szükséges

V_{k}

feszültség, tehát az áram‐feszültség karakterisztikának hiszterézise van. Például

η = 0, 6

értékű ütközési szám esetén

V_{c} \approx 0,485 \cdot V_{k}

. Az ábra vázlatosan mutatja a rendszer karakterisztikáját és a hiszterézist.

2. feladat. Felemelkedő ballon

(a)

Felhasználva az ideális gáz állapotegyenletét,

n

mól hélium gáz térfogata

p + Δ p

nyomáson és

T

hőmérsékleten

\begin{matrix} V = \frac{n R T}{p + Δ p}, \end{matrix}

míg

n'

mól levegő térfogata

p

nyomáson és

T

hőmérsékleten

\begin{matrix} V = \frac{n' R T}{p} . \end{matrix}

Így a ballon kiszorít

n' = n \frac{p}{p + Δ p}

mól levegőt, melynek súlya

M_{lev} n' g

. A kiszorított levegő súlya megegyezik a felhajtóerővel, azaz

\begin{matrix} F_{fel} = M_{lev} n g \frac{p}{p + Δ p} . \end{matrix}

(b)

z

magasságkülönbségből származó nyomásváltozás

- ϱ g z

, ha a levegő

ϱ

sűrűsége állandó. Ha a sűrűség a magasság függvényeként változik, akkor a következő egyenletet használhatjuk:

\begin{matrix} \frac{d p}{d z} = - ϱ g = - \frac{ϱ_{0} T_{0}}{p_{0}} \frac{p}{T} g, \end{matrix}

ahol az egyesített gáztörvényt

\frac{ϱ T}{p} = állandó

alakban használtuk. Ha ebbe az egyenletbe behelyettesítjük a feladatban megadott

p (z) = p_{0} {(1 - z / z_{0})}^{η}

összefüggést, illetve a

T (z) = T_{0} (1 - z / z_{0})

függvényt, akkor a deriválás elvégzése után a keresett

η

kitevőt így fejezhetjük ki:

\begin{matrix} η = \frac{ϱ_{0} z_{0} g}{p_{0}} = \frac{1, 16 \cdot 4, 9 \cdot 10^{4} \cdot 9, 8}{1, 01 \cdot 10^{5}} = 5, 52. \end{matrix}

A kérdéses kitevő számértéke tehát két értékes jegy pontossággal: 5,5.

(c)

Amikor

Δ p

nyomáskülönbség mellett a ballon sugarát

r

-ről

(r + d r)

-re növeljük, akkor a rugalmas megnyújtáshoz szükséges munka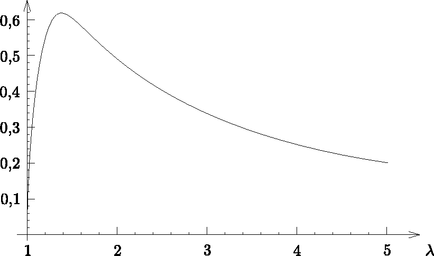

\begin{matrix} d W = 4 π r^{2} Δ p d r, \end{matrix}

míg ugyanekkora

r

sugár mellett a rugalmas energia növekményét a feladatban megadott

U = 4 π r_{0}^{2} κ R T (2 λ^{2} + \frac{1}{λ^{4}} - 3)

energia függvény deriválásával határozhatjuk meg:

\begin{matrix} d W = (\frac{d U}{d r}) d r = 4 π κ R T (4 r - 4 \frac{r_{0}^{6}}{r^{5}}) d r . \end{matrix}

A munkavégzés kétféle kifejezésének egyenlővé tételével kaphatjuk meg a kívánt választ:

\begin{matrix} Δ p = 4 κ R T (\frac{1}{r} - \frac{r_{0}^{6}}{r^{7}}) = \frac{4 κ R T}{r_{0}} (\frac{1}{λ} - \frac{1}{λ^{7}}) . \end{matrix}

A nyomáskülönbség grafikon

λ

(

>

1) függvényében kezdetben élesen növekszik,

λ = 7^{1 / 6} = 1, 38

értéknél maximumot vesz fel, majd nagy

λ

értékeknél

λ^{- 1}

szerint csökken. A következő ábrán a dimenziótlan

\begin{matrix} \frac{Δ p}{\frac{4 κ R T}{r_{0}}} = (\frac{1}{λ} - \frac{1}{λ^{7}}) \end{matrix}

kifejezés ábrázolása látható:

(d)

Írjuk fel az ideális gáz állapotegyenletét:

p_{0} V_{0} = n_{0} R T_{0}

, ahol

V_{0}

a feszítetlen falú ballon térfogatát jelenti. Az

n

mól gázt tartalmazó ballon belső nyomása

V = λ^{3} V_{0}

térfogat mellett

T = T_{0}

hőmérsékleten:

\begin{matrix} p_{belső} = \frac{n R T_{0}}{V} = \frac{n}{n_{0} λ^{3}} p_{0} . \end{matrix}

Másrészt a ballon belső nyomását a

(c)

alkérdésre megadott többletnyomás segítségével is kifejezhetjük

T = T_{0}

hőmérsékleten:

\begin{matrix} p_{belső} = p_{0} + Δ p = p_{0} + \frac{4 κ R T_{0}}{r_{0}} (\frac{1}{λ} - \frac{1}{λ^{7}}) = [1 + a (\frac{1}{λ} - \frac{1}{λ^{7}})] p_{0} . \end{matrix}

A belső nyomás fenti két kifejezését egyenlővé téve határozhatjuk meg az

a

,,ballonparamétert'':

\begin{matrix} a = \frac{\frac{n}{n_{0} λ^{3}} - 1}{λ^{- 1} - λ^{- 7}} . \end{matrix}

A megadott

n / n_{0} = 3, 6

és

λ = 1, 5

numerikus adatokat behelyettesítve, a ballonparaméterre

a = 0, 11

adódik.

(e)

(a)

alkérdésben levezetett felhajtóerő egyensúlyt tart az

M_{teljes} = 1, 12

kg tömegre ható nehézségi erővel, ami a következő összefüggésre vezet:

\begin{matrix} \frac{p}{p + Δ p} = \frac{M_{teljes}}{M_{lev} \cdot n} . \end{matrix}

Másrészről, ha a

V = \frac{4}{3} π r^{3} = λ^{3} \frac{4}{3} π r_{0}^{3} = λ^{3} V_{0}

térfogatú ballon belsejében lévő héliumra újra alkalmazzuk az ideális gáz állapotegyenletét, akkor tetszőleges külső

p

nyomás és

T

hőmérséklet esetén a ballonban lévő

n

mól héliumra felírhatjuk:

\begin{matrix} (p + Δ p) λ^{3} = \frac{n R T}{V_{0}} = p_{0} \frac{T}{T_{0}} \frac{n}{n_{0}} . \end{matrix}

Ha a fenti két összefüggés mellett felhasználjuk a

(c)

alkérdésben a nyomáskülönbségre megkapott formulát, akkor meghatározhatjuk a három ismeretlen mennyiséget, vagyis

p

Δ p

és

λ

értékét mint a

T

hőmérséklet és egyéb adatok függvényét.
A fenti két összefüggés összevetéséből a felhajtóerő‐súly egyensúlyra egy újabb feltételt kapunk:

\begin{matrix} \frac{p}{p_{0}} \frac{T_{0}}{T} λ^{3} = \frac{M_{teljes}}{M_{lev} \cdot n_{0}} . \end{matrix}

Ezek után használjuk fel a

(c)

alkérdésben a nyomáskülönbségre megkapott formulát és az ideális gázegyenletből kapott összefüggést:

\begin{matrix} p λ^{3} + \frac{4 κ R T}{r_{0}} λ^{2} (1 - λ^{- 6}) = p_{0} \frac{T}{T_{0}} \frac{n}{n_{0}}, \end{matrix}

illetve ezt átrendezve és felhasználva a korábban bevezetett

a

,,ballonparamétert'':

\begin{matrix} \frac{p}{p_{0}} \frac{T_{0}}{T} λ^{3} = \frac{n}{n_{0}} - a λ^{2} (1 - λ^{- 6}) . \end{matrix}

Így az előzőleg a felhajtóerő-súly egyensúlyra kapott feltétellel megegyező bal oldalú összefüggésre jutottunk. A jobb oldalak egyenlővé tételével olyan egyenlethez juthatunk, amely már csak a

λ

lineáris méretnövekedési arányt tartalmazza:

\begin{matrix} λ^{2} (1 - λ^{- 6}) = \frac{1}{a n_{0}} (n - \frac{M_{teljes}}{M_{lev}}) = 4,54. \end{matrix}

Az egyenlet megoldása akkor egyszerű, ha közelítést (belátható, hogy nagyon jó közelítést) használunk:

\begin{matrix} λ^{2} \approx \frac{4, 54}{1 - 4, 54^{- 3}} \approx 4, 54 \to λ_{f} ≅ 2, 13. \end{matrix}

A ballon maximális emelkedési magasságát úgy kaphatjuk meg, ha a felhajtóerő‐súly egyensúlyra kapott feltételben

(\frac{p}{p_{0}} \frac{T_{0}}{T})

helyére beírjuk a nyomás és a hőmérséklet magasságfüggését, amit a

(b)

alkérdésben ismerhettünk meg:

\begin{matrix} \frac{p}{p_{0}} \frac{T_{0}}{T} λ_{f}^{3} = {(1 - \frac{z_{f}}{z_{0}})}^{η - 1} λ_{f}^{3} = \frac{M_{teljes}}{M_{lev} \cdot n_{0}} = 3, 10. \end{matrix}

Felhasználva, hogy

λ_{f} = 2, 13

és

(η - 1) = 4, 5

, a ballon maximális emelkedési magasságára

\begin{matrix} z_{f} = (49 km) \cdot (1 - {[\frac{3, 10}{2, 13^{3}}]}^{\frac{1}{4, 5}}) = 10, 9 km. \end{matrix}

A ballon tehát mintegy 11 km magasságra emelkedik, és lineáris mérete

λ_{f} = 2, 1

-szeresére növekszik.

3. feladat. Atomi erő mikroszkóp

(a)

z (t) = A sin (ω t - Φ)

függvényt behelyettesítve a szinuszos gerjesztéssel csillapított kényszerrezgést leíró

m \ddot{z} + b \dot{z} + m ω_{0}^{2} z = F_{0} sin (ω t)

egyenletbe, és

sin (ω t - Φ)

-re,

cos (ω t - Φ)

-re alkalmazva az addíciós azonosságokat, rendezés után azt kapjuk, hogy:

\begin{matrix} {\overset{}{\overset{︷}{(b A ω sin Φ + m A (ω_{0}^{2} - ω^{2}) cos Φ - F_{0})}}}_{}^{0} sin (ω t) + & (1) \\ + {\underset{︸}{(- m A (ω_{0}^{2} - ω^{2}) sin Φ + b A ω cos Φ)}}_{0}^{} cos (ω t) = 0. \end{matrix}

Ez az egyenlet csak úgy állhat fenn minden

t

időpillanatban, ha mindkét kapoccsal jelölt kifejezés zérus. Ebből az

A

amplitúdóra valamint a

Φ

fázis tangensére a

\begin{matrix} tg Φ = \frac{b ω}{m (ω_{0}^{2} - ω^{2})}, A = \frac{F_{0}}{\sqrt[]{b^{2} ω^{2} + m^{2} {(ω_{0}^{2} - ω^{2})}^{2}}} \end{matrix}

(2)

megoldás adódik. Speciálisan az

ω = ω_{0}

,,rezonanciafrekvencián'':

\begin{matrix} Φ = \frac{π}{2}, A = \frac{F_{0}}{b ω_{0}} . \end{matrix}

(3)

Megjegyezzük, hogy a rezonanciafrekvencia szó itt kicsit félrevezető, ugyanis (2) második összefüggése szerint nem zérus csillapítás mellett (

b > 0

) az

A (ω)

amplitúdó a maximumát nem

ω_{0}

, hanem

ω_{{max}_{}^{}} = ω_{0} \sqrt[]{1 - \frac{b^{2}}{2 m^{2} ω_{0}^{2}}}

értéknél veszi fel. Azonban a feladatban szereplő

ω_{0} ≫ \frac{b}{m} > 0

feltevés mellett, azaz kis csillapításnál

ω_{max} \approx ω_{0}

, ezért a feladat további részében is ,,rezonanciafrekvencián'' kicsit pongyolán a gerjesztés és csillapítás nélkül létrejövő rezgés

ω_{0}

frekvenciáját értjük.

(b)

2 sin α sin β = cos (α - β) - cos (α + β)

azonosság felhasználásával a lock-in erősítőben létrejövő szorzat jel a következő alakban írható:

\begin{matrix} V_{i} V_{R} & = V_{i 0} sin (ω_{i} t - Φ_{i}) V_{R 0} sin (ω t) = & (4) \\ = \frac{V_{i 0} V_{R 0}}{2} (cos [(ω_{i} - ω) t - Φ_{i}] - cos [(ω_{i} + ω) t - Φ_{i}]) . \end{matrix}

Általában mindkét koszinusz függvény időátlaga nulla. A szorzat jelnek csak az

ω_{i} = ω

speciális esetben van egyenfeszültségű komponense, ugyanis ekkor az első koszinusz függvény argumentuma független az időtől. Ekkor a kimenő jel egyenfeszültségű komponense:

\begin{matrix} \frac{V_{i 0} V_{R 0}}{2} cos Φ_{i} . \end{matrix}

(5)

Megjegyezzük, hogy a fenti számolás rávilágít a lock-in erősítési technika lényegére. Tegyük fel ugyanis, hogy a

V_{i}

bemenő jelet nagy, esetleg magánál a

V_{i 0}

jelamplitúdónál is nagyobb véletlen zaj terheli. Hagyományos módon ekkor nem tudnánk kiszűrni a mérendő jelet a háttérzajból. Azonban a lock-in detektor kimenetén a véletlen zaj nulla időátlagú jelet ad, úgy, ahogy

ω_{i} \neq ω

esetén is zérus a kimeneti jel időátlaga. Pontosabban, a zajt is, mint ahogy minden más jelet, fel lehet bontani különböző frekvenciájú szinuszos jelek összegére (ezt hívják Fourier‐analízisnek). A lock-in detektor egy igen erősen szelektív frekvenciaszűrőként működik, a referencia jel

ω

frekvenciájának egy nagyon szűk környékén átengedi a jelet, míg minden más frekvenciájú Fourier-komponenst elnyom. Így a zaj nagy része nem jelenik meg a kimeneten, míg az

ω

frekvenciájú jel zavartalanul átjut a lock-in erősítőn.

(c)

(a)

pont (3) eredménye szerint az

ω_{0}

rezonanciafrekvencián az érzékelő kar kitérése

π / 2

fázissal késik a gerjesztéshez képest. Így az

F = c_{1} V'_{R} = c_{1} V_{R 0} sin (ω t + \frac{π}{2})

gerjesztés hatására a fotoérzékelő kimenő jele

V_{i} = c_{2} z = c_{1} c_{2} \frac{V_{R 0}}{b ω_{0}} sin (ω t)

alakú, azaz azonos fázisban van a

V_{R} = V_{R 0} sin (ω t)

referencia jellel. Így az (5) formulában

Φ_{i} = 0

, tehát a lock-in erősítő egyenáramú kimenő jele:

\begin{matrix} \frac{V_{i 0} V_{R 0}}{2} cos 0 = c_{1} c_{2} \frac{V_{R 0}^{2}}{2 b ω_{0}} . \end{matrix}

(6)

(d)

Δ m

tömegváltozás hatására az új rezonanciafrekvencia

\begin{matrix} \sqrt[]{\frac{k}{m}} {(1 + \frac{Δ m}{m})}^{- \frac{1}{2}} \approx ω_{0} (1 - \frac{Δ m}{2 m}), tehát Δ ω_{0} = - ω_{0} \frac{Δ m}{2 m} . \end{matrix}

(7)

A rezonanciafrekvencia és a tömegváltozás hatására (2) első egyenletének értelmében a gerjesztés és a kialakult kényszerrezgés közti

Φ

fázis is megváltozik. Kezdetben (a tömegváltozás előtt) a rendszer

ω = ω_{0}

rezonanciafrekvencián működött, és a fázistolás értéke

Φ = π / 2

volt. A tömeg megváltozása nem befolyásolja az

ω = ω_{0}

gerjesztési frekvenciát, azonban a fázis, a tömeg, ill. a rezonanciafrekvencia a

ϕ \to \frac{π}{2} + Δ ϕ

m \to m + Δ m

, ill.

ω_{0} \to ω_{0} + Δ ω_{0}

formulának megfelelően eltolódik. Ezeket a helyettesítéseket elvégezve (2) első egyenletében, és

Δ Φ

, ill.

Δ m

kicsiny értékei mellett alkalmas közelítést használva

\begin{matrix} {\underset{︸}{tg (\frac{π}{2} + Δ Φ)}}_{\approx - 1 / Δ Φ}^{} = b ω_{0} / {\underset{︸}{([m + Δ m] [{(ω_{0} + Δ ω_{0})}^{2} - ω_{0}^{2}])}}_{\approx - Δ m ω_{0}^{2}}^{}, \end{matrix}

(8)

adódik, ahonnan a fáziseltolódásból még éppen kimutatható tömegváltozás:

\begin{matrix} Δ m = \frac{Δ Φ b}{ω_{0}} = \frac{b}{m} \cdot \frac{m^{\frac{3}{2}}}{k^{\frac{1}{2}}} \cdot Δ Φ = 10^{3} \cdot 10^{- 18} \cdot \frac{π}{1800} kg = 1, 7 \cdot 10^{- 18} kg . \end{matrix}

(9)

(e)

Mivel a minta által kifejtett

f (h) \approx f (h_{0}) + c_{3} (h - h_{0})

erő is lineárisan függ a kar elmozdulásától, csakúgy, mint a rugóerő, a két erő eredője egy új,

k'

rugóállandójú effektív rugóerőnek tekinthető, és ez határozza meg az új rezonanciafrekvenciát. Pontosabban a

h_{0}

egyensúlyi helyzettől mért

z = h - h_{0}

kitérésre a következő mozgásegyenlet írható fel:

\begin{matrix} m \ddot{z} + b \dot{z} + m ω_{0}^{2} z = F_{0} sin (ω t) + c_{3} z . \end{matrix}

(10)

(Az új egyensúlyi helyzetben az

f (h_{0})

konstans kiesik az egyenletből.)
Látható, hogy az új effektív rugóállandó

k' = m ω_{0}^{2} - c_{3}

, így az új rezonanciafrekvencia:

\begin{matrix} ω'_{0} = \sqrt[]{\frac{k'}{m}} = ω_{0} \sqrt[]{1 - \frac{c_{3}}{m ω_{0}^{2}}}, és Δ ω_{0} = ω'_{0} - ω_{0} \approx - \frac{c_{3}}{2 m ω_{0}} . \end{matrix}

(11)

(f)

A maximális frekvenciaeltolódás akkor jön létre, amikor a mikroszkóp érzékelő tűje éppen a csapdázott elektron fölött van. Ekkor a minta és a kar közti Coulomb-erő

f (h) = k_{e} \frac{q Q}{h^{2}}

. Feltéve, hogy a kar rezgésének amplitúdója jóval kisebb, mint a két töltés

d_{0}

távolsága, az

f (h)

függvényt linearizálhatjuk az egyensúlyi helyzet körül. A meredekségre a

\begin{matrix} c_{3} = \frac{d f}{d h} |_{h = d_{0}} = - 2 k_{e} \frac{q Q}{d_{0}^{3}} \end{matrix}

(12)

érték adódik, ahonnan (11) felhasználásával a frekvenciaeltolódás

Δ ω_{0} \approx \frac{k_{e} q Q}{m ω_{0} d_{0}^{3}}

. Innen a keresett távolság az adatok behelyettesítésével:

\begin{matrix} d_{0} = \sqrt[3]{\frac{k_{e} q Q}{m ω_{0} Δ ω_{0}}} = 4, 1 \cdot 10^{- 8} m = 41 nm . \end{matrix}

(13)

Az 1985-ben G. Binnig, C. F. Quate és Ch. Gerber által felfedezett atomi erő mikroszkóp² (Atomic Force Microscope, AFM) két tekintetben is a pásztázó alagútmikroszkóp (Scanning Tunneling Microscope, STM) kishúgának tekinthető: egyrészt a két berendezés felfedezői részben azonosak³; másrészt, a két berendezés működési elvének is vannak hasonló vonásai. Mindkét eszközben egy nagyon kisméretű, éles hegyű tűt mozgatnak a minta fölött, soronként pásztázva végig a minta felszínét. Mindkét berendezés alkalmas atomi méretű mintázatok detektálására. Az STM-ben a mért jel a tű és a minta között folyó áram ingadozása, míg az AFM-ben a tűre ható mechanikai erő finom változásait érzékelik. Így az atomi erő mikroszkóp lényegében úgy tapogatja le a minta felszínét, mint ahogy a régi lemezjátszók tűje érzékeli a hangjeleket tartalmazó mikrobarázdákat a bakelit hanglemezen.
A fenti feladat az AFM egy fejlettebb változatának elvi működéséhez kapcsolódik; az érzékelő tű nem kerül direkt kontaktusba a minta felszínével, hanem ahhoz nagyon közel gerjesztett rezgőmozgást végez, és a rezgés fázisának a minta hatására bekövetkező eltolódását detektálják.
Az AFM technikának több jelentős előnye is van a néhány évvel korábban felfedezett STM-mel szemben: a mintát nem kell légüres térbe helyezni, vizsgálhatók levegőben, vagy folyadék alatt levő minták is; a mintának nem kell elektromos vezetőnek lennie; a vizsgálat kevésbé roncsoló hatású, így vizsgálhatók lágyabb minták, például biológiai szövetek is.

A kísérleti feladat megoldása

A feladatban egy úgynevezett ,,mechanikai fekete doboz'' fizikai paramétereit kellett meghatározni. A ,,mechanikai fekete doboz'' egy lezárt csőből állt, melyben egy golyó helyezkedett el. A golyó két rugó segítségével a cső két végéhez volt erősítve. A feladat lényegében az volt, hogy meg kellett mérni a golyó tömegét és a két rugóállandót (természetesen a lezárt cső felnyitása nélkül).
Mérleggel határozhatjuk meg a cső-golyó rendszer együttes tömegét. Vízszintes helyzetben a csövet kiegyensúlyozva (kétoldalú emelőként használva), megkaphatjuk a cső-golyó rendszer tömegközéppontját (hány centiméterre van a cső közepétől). Egyszerű forgatónyomaték egyensúlyból kiszámíthatjuk a golyó tömegének és a cső középpontjától mért távolságának a szorzatát. Ezzel túljutunk az első részfeladaton.
A golyó tömegének meghatározásához a csövet forgóasztalra kell tenni, melyet egy csigán átvetett fonálhoz rögzített test segítségével hozhatunk forgásba. Ha a test függőleges elmozdulását ábrázoljuk a test sebesség-négyzetének a függvényében, akkor a következő grafikonhoz juthatunk: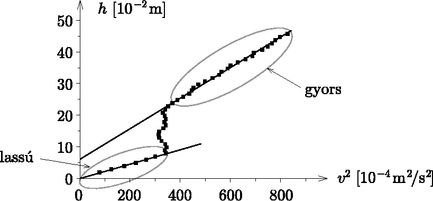

Az ábrán három szakaszt különböztethetünk meg: a lassú, az átmeneti és a gyors szakaszt. Lassú mozgáskor a tapadási súrlódás megakadályozza a golyó elmozdulását a csőben, az átmeneti szakaszban a golyó fokozatosan kijjebb csúszik, a gyors mozgáskor viszont a cső végénél megakad. A grafikon alapján megállapíthatjuk, hogy a lassú forgás tartományában

h

egyenesen arányos

v^{2}

-tel (

h = C v^{2}

), míg a gyors forgás tartományában

h = A v^{2} + B

egyenlettel írható le. Az

A

B

és

C

együtthatók mérhetőek.
A forgó mozgás energetikai leírásával olyan egyenletekhez juthatunk, melyek segítségével az

A

B

és

C

együtthatók meghatározhatók, illetve az előző részben megkapott tömeg-távolság szorzat segítségével a golyó tömege is kiszámítható.
A rugóállandókat úgy kaphatjuk meg, ha a ,,mechanikai fekete dobozt'', vagyis a csövet előbb egyik, majd másik végénél felfüggesztjük, és fizikai ingaként lengetjük. Megmutatható, hogy a golyó vízszintes egyensúlyi helyzetéből történő elmozdulása ugyanakkora, akármelyik vége körül lengetjük a csövet. A mért lengésidőkből ez az elmozdulás, majd ebből a két rugó úgynevezett effektív rugóállandója meghatározható.
A két rugóállandót külön-külön úgy számíthatjuk ki, ha figyelembe vesszük az effektív rugóállandót, továbbá azt is, hogy az előző vizsgálatok nyomán már kiszámíthatjuk a golyó pontos egyensúlyi helyét a cső vízszintes helyzetében.
Összefoglalásképpen érdemes megemlítenünk, hogy ez a feladat méréstechnikailag nem volt könnyű, szokatlan volt a digitális óra használata, önállóan kellett létrehozni az egyes elrendezéseket, ám ezek a mérési nehézségek eltörpültek a feladat által megkívánt igen szövevényes elméleti számítások okozta gondokhoz képest.

¹A feladatok szövegét a KöMaL októberi számában közöltük.

²Phys. Rev. Lett., 56, 930‐933 (1986).

³A pásztázó alagútmikroszkópot G. Binnig és H. Rohrer fedezte föl 1981-ben; felfedezésükért 1986-ban Nobel-díjat kaptak.