Cím: VII. román-magyar előolimpiai fizikaverseny
Füzet: 2004/október, 437 - 439. oldal  PDF  |  MathML 
Témakör(ök): Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

2. feladat.1
Biliárdgolyók ütközése (10 pont). Ebben a feladatban két biliárdgolyó ütközését vizsgáljuk.
A biliárdasztal közepén nyugszik az első (A) golyó. A második (B) golyó az asztal középső hossztengelye mentén 1 méterre áll az elsőtől. A B golyót vízszintes dákóval úgy lökjük meg, hogy a dákó a golyó középpontján átmenő vízszintes síktól félsugárnyi távolságban ütközik közel pillanatszerűen a golyóval. Ezt követően a két golyó között centrális, egyenes ütközés jön létre, amely tökéletesen rugalmasnak és szintén pillanatszerűnek tekinthető. A B golyó az ütközést követően megáll, és az asztal közepén állva is marad. A golyók között a súrlódás elhanyagolható, a golyók és az asztal közötti súrlódási együttható értéke 0,3.
a) Legalább mekkora a tapadási súrlódási együttható értéke a dákó vége és a második golyó között? (2 pont)
b) Mekkora sebességgel indítottuk el a dákóval a B golyót? (5 pont)
c) Mekkora sebességgel éri el az A golyó a biliárdasztal szélét? (3 pont)

 
3. feladat.
Visszapillantó tükör (5 pont). Az autók középső visszapillantó tükre elforgatható, így éjszaka a vezetőket nem vakítja el a mögöttük haladó járművek erős fénye, mert az elfordított tükörrel a vezető ugyanazt a képet gyengítettebben látja. Ezt a hatást a középső tükörrel úgy érik el, hogy a tükör külső síküveg felülete és a belső foncsorozott (ezüstözött) szintén sík felülete nem párhuzamos, hanem valamekkora szöget zár be egymással.
Mekkora ez a szög, ha a tükröt 6 fokkal lehet elforgatni, és az üveg törésmutatója 1,5?
Útmutatás: A közelítő számítás során tekintsünk el a fény vízszintes síkban történő eltérítésétől, vagyis kezeljük a problémát úgy, mintha a fénysugarak tisztán függőleges síkban haladnának, és a tükör elfordításakor alkalmazott vízszintes forgástengely erre a síkra merőleges lenne.
 
4. feladat.
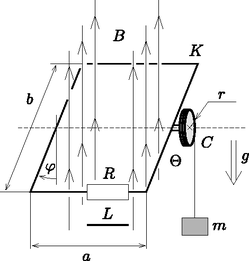
Forgó keret (10 pont). Az A=a×b területű K fémkeret az r sugarú C csigához van rögzítve. A két test együtt vízszintes tengely körül súrlódásmentesen forog. A keret síkjának a függőlegessel bezárt szögét jelölje φ, és a rendszer tehetetlenségi nyomatéka a forgástengelyre vonatkoztatva legyen Θ. A csigára nyújthatatlan, elhanyagolható tömegű fonalat csévélünk, melynek a végére m tömegű testet akasztunk. A nehézségi gyorsulás g. A keretet B indukciójú, függőleges irányú homogén mágneses térbe helyezzük.
 
 

Az A, r, Θ, m, g és B paramétereket az egész feladat során adottnak tekinthetjük.
 
Ellenállás. Ebben a részfeladatban a zárt fémkeret (ohmikus) elektromos ellenállása R. Feltesszük, hogy a keretben indukált áram mágneses tere jóval kisebb, mint a külső B tér.
1. Határozzuk meg a keretben indukált I(t) áram értékét az idő függvényében, ha a keretet állandó ω szögsebességgel forgatjuk! (0,6 pont)
2. Határozzuk meg a keretre ható elektromágneses erők M(t) forgatónyomatékát az idő függvényében, ha a keretet állandó ω szögsebességgel forgatjuk! (0,6 pont)
3. Határozzuk meg a forgatónyomaték időátlagát! (0,6 pont)
A keretet függőleges helyzetbe állítjuk, és a rendszert (a keretet és a csigán lógó testet) magára hagyjuk. A következő két kérdés megválaszolásánál tételezzük fel, hogy
  Az elektromágneses forgatónyomaték (egy fordulatra vett)  időátlaga jól közelíti a pillanatnyi forgatónyomatékot!  (*)

4. Határozzuk meg a keret ω∞ (átlagos) szögsebességét hosszú idő múlva! (0,6 pont)
5. Határozzuk meg a keret (fordulatonként átlagolt) szögsebességének időfüggését! (1 pont)
6. Vizsgáljuk meg, hogy milyen paraméterértékek mellett jogos a (*) feltevés? (1 pont)
7. Írjuk föl a keret forgómozgásának egzakt mozgásegyenletét, a (*) feltevés felhasználása nélkül! (0,6 pont)
 
Szupravezető. Most tételezzük föl, hogy a keret szupravezető, azaz elektromos ellenállása zérus.
8. Ha megforgatjuk a keretet, feltételezhetjük-e, hogy a keretben folyó áram mágneses tere jóval kisebb, mint a külső B tér? (Válaszunkat indokoljuk!) (0,5 pont)
Legyen a keretnek (mint egymenetes tekercsnek) az önindukciós együtthatója L. A keretet függőleges helyzetbe állítjuk, ekkor a keretben nem folyik áram, és a rendszert magára hagyjuk.
9. Határozzuk meg a keretben folyó I áramot, valamint keretre ható elektromágneses erők M forgatónyomatékát a keret φ elfordulásának függvényében! (1 pont)
10. Írjuk föl a keret forgómozgásának mozgásegyenletét! (0,5 pont)
11. Határozzuk meg a keret ω szögsebességét a keret φ elfordulásának függvényében! (2 pont)
12. Mekkora a keret φmax maximális szögelfordulása a mozgás során? (1 pont)
1A versenyen összesen négy elméleti és két mérési feladat szerepelt. Az 1. elméleti feladatot múlt havi számunkban közöltük. A mérési feladatok egyikében fakockákban elrejtett kis mágnesek közötti erőhatást mérték a versenyzők; a másikban egy villanyvasaló, stopper, hőmérő és kormozásra használható gyertya segítségével a Stefan‐Boltzmann-törvény állandóját határozták meg.