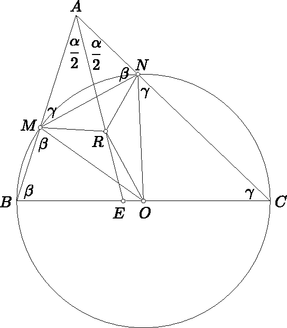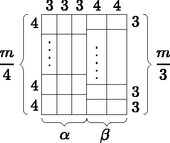Cím: A 45. Nemzetközi Matematika Diákolimpia feladatainak megoldásai
Füzet: 2004/október, 386 - 395. oldal  PDF  |  MathML 
Témakör(ök): Nemzetközi Matematikai Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A hagyományoknak megfelelően ebben az évben is közöljük a nyári matematikai diákolimpia feladatainak a megoldásait úgy, ahogyan a legilletékesebbek, a magyar csapat tagjai leírták. Közreműködésüket köszönjük és ezúton is gratulálunk eredményeikhez.

 
A szerkesztőség

 

1. Legyen ABC hegyesszögű háromszög, amiben AB≠AC. A BC átmérőjű kör az AB, ill. AC oldalakat az M, ill. N pontokban metszi. Jelölje O a BC oldal középpontját. A BAC∢ és MON∢ szögek szögfelezői az R pontban metszik egymást. Bizonyítsuk be, hogy a BMR és CNR háromszögek körülírt köreinek van olyan közös pontja, ami a BC oldalon fekszik.
 
 

Paulin Roland megoldása. Thálész tétele alapján BMC∢=BNC∢=90∘, így M és N a magasságok talppontjai, melyek az ABC háromszög AB, illetve AC oldalainak belsejében vannak, mert a háromszög hegyesszögű.
BMNC húrnégyszög, így AMN∢=γ, ANM∢=β. OBM és OCN egyenlő szárú háromszögekben OMB∢=β, ONC∢=γ, vagyis OMN∢=ONM∢=α, MON∢=π-2α.
 
 

Belátjuk, hogy a BAC és MON szögek szögfelezői ‐ e és f ‐ nem párhuzamosak, így R egyértelműen meghatározott. e∥f esetén legyen f∩AC=D. A DOC háromszögben D-nél α2, C-nél γ, O-nál
CON∢+NOM∢2==(π-2γ)+π-2α2=32π-2γ-α


szög van, így a szögösszeg
π=α2+γ+32π-2γ-α.
Rendezve:
α2+γ=π2⇒α+2γ=π=α+β+γ⇒γ=β⇒AB=AC.
Ezt a feltétel kizárja, így e∦f.
Legyen I az OMN háromszög beírt körének középpontja. IMN∢=INM∢=α2 miatt MIN∢=π-α, ezért AMIN húrnégyszög, így IAN∢=IMN∢=α2. Tehát I∈e, ugyanakkor I∈f is teljesül, ezért R=I.
Legyen E=e∩BC. Ez a BC oldal egy belső pontja. Belátjuk, hogy a BMR és a CNR háromszögek körülírt köre is átmegy E-n. REB∢=AEB∢=π-β-α2, REC∢=AEC∢=π-γ-α2, míg RMB∢=β+α2, RNC∢=γ+α2, így RMB∢+REB∢=RNC∢+REC∢=π. Azaz RMBE és RNCE húrnégyszögek, így az RMB és az RNC háromszögek körülírt körének van közös pontja a BC oldalon.
 
2. Határozzuk meg az összes olyan valós együtthatós P(x) polinomot, amely kielégíti a
P(a-b)+P(b-c)+P(c-a)=2P(a+b+c)
egyenlőséget, valahányszor a, b, c olyan valós számok, amelyekre teljesül
ab+bc+ca=0.

 
 

Hubai Tamás megoldása. Ha a=b=c=0, akkor a feltétel teljesül, így 3P(0)=2P(0), vagyis P(0)=0. A feltétel nyilván akkor is teljesül, ha b=c=0, és így P(a)+P(0)+P(-a)=2P(a), ahonnan P(-a)=P(a) adódik minden valós a-ra. A P(x) polinomfüggvény tehát páros, ami csak úgy lehetséges, ha minden páratlan fokú tagja nulla. (A P(-a)=P(a) feltételt átrendezve ugyanis azt kapjuk, hogy P(x)-P(-x) az azonosan nulla polinom, ebben a különbségben pedig éppen a P(x) páratlan fokú tagjai szerepelnek.)
Legyen ezután Q(x) az a polinom, amelyben P(x) tagjai szerepelnek félakkora kitevővel, azaz amelyre Q(x2)=P(x) és nézzük meg, minek kell teljesülnie a Q(x) polinomra. Az a, b, c közti összefüggést felhasználva csökkentsük a változók számát. Vezessük be az x és y változókat a következőképpen: legyen a=x+y+c, b=y+c. Ilyen x és y nyilván minden a, b és c hármashoz létezik, másrészt x és y bármely értékére van olyan a, b, c számhármas, amelyre teljesül a feltétel. Ez egész pontosan azt jelenti, hogy az a=x+y+c, b=y+c, ab+bc+ca=0 egyenletrendszernek létezik (a,b,c) megoldása. Behelyettesítve ugyanis az (x+y+c)(y+c)+(y+c)c+c(x+y+c)=0 egyenletet kapjuk, ami rendezés után a c-ben másodfokú:
3c2+(2x+4y)c+(xy+y2)=0,
a diszkriminánsa, 4x2+4xy+4y2=2(x2+y2+(x+y)2) pedig nem negatív.
Fejezzük ki a feltételben szereplő mennyiségeket az új változók, x és y segítségével: a-b=x, b-c=y, c-a=-x-y, illetve
(a+b+c)2=a2+b2+c2+2ab+2bc+2ca=
(felhasználva, hogy a feltétel szerint ab+bc+ca=0 és tovább alakítva)
=a2+b2+c2-ab-bc-ca=(a-b)2+(b-c)2+(c-a)22==x2+y2+(x+y)22=x2+y2+xy.
A P polinomra tehát, mint láttuk, akkor és csak akkor teljesülnek a feladat feltételei, ha bármely valós x, y számpárra fennáll, hogy
P(x)+P(y)+P(x+y)=2P(x2+y2+xy).
(Vegyük észre, hogy a bal oldal harmadik tagja eredetileg P(c-a)=P(-x-y), ami most azért írható P(x+y) alakban, mert a P páros függvény.)
A Q(x) polinomra nézve ez azt jelenti, hogy
Q(x2)+Q(y2)+Q(x2+y2+2xy)=2Q(x2+y2+xy).(1)
Az egyenlőségben x két polinomja áll, melyekben az együtthatók az y változó polinomjai. Tegyük fel, hogy a Q(x) polinom n-edfokú és legyen az n>1. A Q(x) főegyütthatójával (1)-ben lehet osztani, föltehető tehát, hogy az 1. Mivel (1)-ben két polinom egyenlősége áll, a két oldalon az x változó minden előforduló hatványának egyenlő az együtthatója. Nekünk az x2n-2 tagot érdemes figyelnünk. Ha xn-1 együtthatója a Q(x)-ben λ, akkor x2n-2 együtthatói (1) két oldalán:
λ+0+(λ+ny2+(n2)⋅4y2)=2(λ+ny2+(n2)⋅y2).
Rendezés után innen 2⋅(n2)=n, azaz n>1 miatt n=2 adódik. Ez azt jelenti, hogy n≤2, a Q(x) tehát legfeljebb másodfokú, a P(x) így legfeljebb negyedfokú páros polinom, amelynek a konstans tagja nulla: P(x)=α⋅x4+β⋅x2.
Megmutatjuk, hogy ezekre a polinomokra teljesül a feladat feltétele. Ezt elég abban a két speciális esetben igazolni, ha P(x)=x4, illetve P(x)=x2. Könnyen ellenőrizhető ugyanis, hogy két megoldás összege, illetve egy megoldás számszorosa is megoldás, így pedig valamennyi adott alakú polinomot megkapjuk a fenti két speciális polinomból.
Ha P(x)=x4, akkor
2P(a+b+c)-P(a-b)-P(b-c)-P(c-a)==2(a+b+c)4-(a-b)4-(b-c)4-(c-a)4==12(a3b+b3c+c3a+ab3+bc3+ca3)+6(a2b2+b2c2+c2a2)++24(a2bc+b2ac+c2ab)==6(ab+bc+ca)2+12(a2+b2+c2)(ab+bc+ca)=0.
Ha pedig P(x)=x2, akkor
2P(a+b+c)-P(a-b)-P(b-c)-P(c-a)==2(a+b+c)2-(a-b)2-(b-c)2-(c-a)2==2(a2+b2+c2+2ab+2bc+2ca)-(a2+b2-2ab)--(b2+c2-2bc)-(c2+a2-2ca)=6(ab+bc+ca)=0.
Ezzel a megoldást befejeztük, a keresett polinomok a P(x)=α⋅x4+β⋅x2 alakba írhatók, ahol α és β tetszőleges valós számok.
 
3. Nevezzük horognak az alábbi ábrán látható, hat egységnégyzetből álló alakzatot
 
 
valamint minden olyan alakzatot, amely ebből forgatásokkal és tükrözésekkel kapható.
Határozzuk meg az összes olyan m×n-es téglalapot, ami lefedhető horgokkal úgy, hogy
•a lefedés hézagmentes és átfedések nélküli,
•semelyik horognak nem nyúlik semelyik része sem a téglalapon kívülre.

 
 

Rácz Béla András megoldása. Feltehetjük, hogy egy lefedett téglalap m, n oldalai egészek, illetve hogy minden horog éppen hat egységnégyzetet fed le, amelyek szerepelnek az egész téglalap egységnégyzetekre bontásában.*
 

 
1. ábra
 

Tekintsünk egy horgot és a hozzá tartozó ,,középső'' mezőt (1. ábra). Ez a mező a lefedni kívánt téglalap belsejében van, egy másik horognak tehát le kell fednie. Könnyen ellenőrizhető, hogy ez csak kétféle módon lehetséges (2a., 2b. ábra).
 
 

Az egymás ,,közepét'' kölcsönösen lefedő két horgot ,,összeragasztva'' kétféle 12 területű csempét kapunk: a 3×4-es téglalapot és ennek ,,ferde'' formáját. A téglalap területe, m⋅n tehát osztható 12-vel, hiszen a lefedésben nyilván egész számú csempe vesz részt. Így 3∣m vagy 3∣n. Az általánosság megszorítása nélkül föltehető, hogy 3∣m. Vizsgáljuk most már azt, hogy m, illetve n a 2-nek milyen hatványával osztható.
(I) 4∣m, azaz 12∣m.
Ha n=1 vagy 2, akkor a lefedés nyilván lehetetlen, ha n=3 vagy 4, akkor a téglalap már 3×4-es csempékkel is lefedhető (3. ábra).
 

 
3. ábra
 

Ha n=5, akkor a két ,,szomszédos'' sarokmezőt két különböző csempe fedi csak le, ezek viszont nem férnek el átfedés nélkül (4. ábra).
 

 
4. ábra
 

Ha n≥6, akkor ‐ 12∣m esetén ‐ az n×m-es téglalap lefedhető 3×4-es csempékkel. Ha ugyanis n=3α+4β, ahol α,β∈N, akkor a megfelelő lefedés az 5. ábrán látható. Ha pedig n≥6, akkor létezik a megfelelő felbontás, hiszen 6=3+3, 7=3+4, 8=4+4, végül ha n előáll ilyen alakban, akkor nyilván n+3 is.
 

 
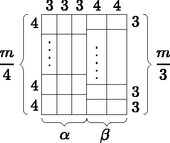5. ábra
 

Vegyük észre, hogy lényegében újra igazoltuk a már tárgyalt n=3,4 eseteket.
(II) Ha 4∣n, akkor a lefedés nyilván megvalósítható 3×4-es csempékkel (6. ábra).
 

 
6. ábra
 

(III) Ha sem (I) sem pedig (II) nem teljesül, azaz 4∤m és 4∤n, akkor 4∣mn miatt m is és n is páros. Azt állítjuk, hogy ilyenkor a megfelelő lefedésben szükségképpen páros sok csempe vesz részt és így a téglalap területe osztható 8-cal. Ez viszont nem lehetséges, ha egyik oldal hossza sem osztható 4-gyel, így ilyenkor nincs megfelelő lefedés.
Színezzük ki a lefedett téglalap mezőit úgy, hogy minden negyedik oszlop fekete legyen, a többi pedig fehér. Ekkor a fekete mezők száma páros, hiszen minden oszlopban páros sok mező van. Csoportosítsuk a lefedésben részt vevő csempéket a 7. ábra szerint.
 

 
7. ábra
 

Minden ,,álló'' csempe páros sok fekete mezőt fed le, egy-egy fekvő csempe pedig páratlan sokat (3-at), ezért páros sok ,,fekvő'' csempe vesz részt a lefedésben. Ha pedig az oszlopok helyett minden negyedik sort színezünk feketére, akkor ugyanígy kapjuk, hogy az ,,álló'' csempék száma páros.
Így tehát összesen is páros számú csempe van, a megfelelő lefedés ebben az esetben nem létezik.
Összefoglalva: a lehetséges m és n értékek a következők:
• 3∣m  és  4∣n; és szimmetrikusan • 3∣n  és  4∣m;• 12∣m  és  n≥6;  • 12∣n  és  m≥6.

 
Megjegyzések. 1. Az adott felsorolásban bizonyos (m;n) számpárok többször is előfordulhatnak.
2. Látható, hogy a ,,ferde'' csempéket nem tudjuk hasznosítani, ami egyáltalán lefedhető, ahhoz elegendőek a 3×4-es csempék is.
 
4. Legyen n≥3 egész szám. Legyenek t1,t2,...,tn pozitív valós számok, amelyekre teljesül
n2+1>(t1+t2+...+tn)(1t1+1t2+...+1tn).

Mutassuk meg, hogy ti, tj, tk egy háromszög oldalhosszai minden olyan i, j, k esetén, amikre 1≤i<j<k≤n teljesül.
 
 

Egri Attila megoldása. A bizonyítás indirekt: Tegyük fel, hogy valamilyen a, b és c számokra ta, tb és tc nem egy háromszög oldalai, tehát pl. ta≥tb+tc.
A feladat szerint:
n2+1>(t1+t2+...+tn)(1t1+1t2+...+1tn)=
=n+∑i<j(titj+tjti)=n+∑i<ji,j∉{a;b;c}(titj+tjti)+tatb+tbta+tatc+tcta+tbtc+tctb.
A jobb oldalon a szumma jelen belül használjuk fel, hogy x∈R+-ra x+1x≥2. Így azt kapjuk, hogy
n2+1>n+2⋅[(n2)-3]+tatb+tbta+tatc+tcta+tbtc+tctb.(1)

Belátjuk, hogy az indirekt ta≥tb+tc feltevésből a nyilvánvaló T=tatb+tbta+tatc+tcta+tbtc+tctb≥6 becslésnél erősebb T≥7 is megkapható.
Ehhez használjuk fel, hogy ha p-t rögzítjük és q-t p felé közelítjük, akkor pq+qp értéke csökken. Ez leolvasható az f(q)=pq+qp grafikonjáról (ábra), de közvetlen bizonyítás is nyomban adódik:
pqr(f(q)-f(r))=p2r+q2r-r2p-q2p=(r-p)(q2-rp).
Ha pedig r elválasztja p-t és q-t, akkor a szorzat tényezői azonos előjelűek, így 0≤p,q,r miatt f(q)≥f(r) valóban.
 
 

Ezek után írjunk T-ben ta helyére (tb+tc)-t. Mivel ta≥tb+tc≥tb és ta≥tb+tc≥tc, azért a fentiek szerint ezzel T csökken.
tatb+tbta≥tb+tctb+tctb+tc=1+tctb+tbtb+tc,illetvetatc+tcta≥tb+tctc+tctb+tc=1+tbtc+tctb+tc.
Így T≥2+2(tctb+tbtc)+1≥7, hiszen tctb+tbtc≥2. Ezzel pedig (1) a következőképpen alakul:
n2+1>n+2[(n2)-3]+7=n2+1,
tehát n2+1>n2+1. A kapott ellentmondás azt jelenti, hogy a feladat állítása igaz: minden i<j<k-ra teljesül, hogy ti, tj és tk egy háromszög oldalai.
 
5. Egy ABCD konvex négyszögben a BD átló nem szögfelezője sem az ABC∢, sem a CDA∢ szögnek. A P pont az ABCD négyszög belsejében fekszik, és teljesül rá
PBC∢=DBA∢ésPDC∢=BDA∢.

Bizonyítsuk be, hogy ABCD akkor és csak akkor húrnégyszög, ha AP=CP.
 
 

Kocsis Albert Tihamér megoldása. Először azt látjuk be, hogy ha ABCD húrnégyszög, akkor PA=PC.
Legyen BP és a kör metszéspontja D', DP és a kör metszéspontja pedig B' (1. ábra).
 

 
1. ábra
 

ABD∢=D'BC∢, az AD⌢=D'C⌢ ívekhez tartozó kerületi szögek egyenlők, így D és D' az AC felező merőlegesére tükrösek. Ekkor a BD' és a B'D egyenesek is tükrösek erre a felező merőlegesre, a metszéspontjuk, P tehát rajta van az AC felező merőlegesén és így valóban PA=PC.
A megfordításhoz legyen PA=PC. Belátjuk, hogy a feladat feltételei mellett ABCD húrnégyszög. Először egy segédtételre lesz szükségünk:
Ha adott egy XYZ háromszög és a síkjában egy Q pont, akkor a háromszög csúcsait a Q-val összekötő egyeneseknek az adott csúcson átmenő belső szögfelezőkre vonatkozó tükörképei egy ponton haladnak át (esetleg párhuzamosak). A bizonyítás megtalálható például Reiman István ‐ Dobos Sándor: Nemzetközi Matematikai Diákolimpiák (1959‐2003) (Typotex Kiadó, Budapest) c. könyvének függelékében.
Most a BPD háromszög játssza az XYZ háromszög szerepét, a Q pontét pedig az A pont. DA tükörképe a PDB szög felezőjére éppen a DC egyenes, míg a BA tükörképe a DBP szög felezőjére a BC egyenes. Ez a két egyenes most a C pontban metszi egymást, így a PA egyenesnek a DPB szög felezőjére vonatkozó tükörképe a segédtétel állítása szerint átmegy a C ponton (2. ábra). Ez a tükörkép tehát a CP egyenes.
 

 
2. ábra
 

Ekkor APB∢=180∘-DPC∢, így ha U=PB∩AC és V=DP∩AC, akkor VPC∢=APU∢. Miután a feltétel szerint PA=PC, továbbá PAU∢=PCV∢, így PUV∢=PVU∢, a PUV háromszög egyenlő szárú. Jelölje az AC felező merőlegesét f.
Ekkor PD és PB tükrösek f-re, ez ugyanis a PUV háromszög szimmetriatengelye, a PD és PB egyenesek pedig a szárai.
Legyen a D csúcs tükörképe f-re D'. Az előbbi szimmetria miatt D' illeszkedik a PB egyenesre. A feltétel miatt ABD∢=D'BC∢, tehát az ADD'C szimmetrikus trapézban az egyenlő hosszú AD és D'C szakaszok a B pontból egyenlő szögben látszanak. Az AD szakasz ABD szögű látóköre és a D'C szakasz D'BC szögű látóköre tehát egybevágó, másrészt ez a két kör is szimmetrikus az f-re. Ha egybeesnek, akkor B rajta van ezen a körön, amely egyébként a szimmetrikus ADD'C trapéz körülírt köre és készen vagyunk, ABCD húrnégyszög.
Ha a két látókör nem esik egybe, akkor B metszéspontjuk rajta van a két kör f szimmetriatengelyén. A fenti gondolatmenetet az ADC helyett az ABC háromszögre és a megfelelő B' pontra megismételve kapjuk, hogy ha a négy pont, A, B, C, D nincs egy körön, akkor D is rajta van az f egyenesen. Ha tehát nem igaz az állítás, akkor BD az AC átló felezőmerőlegese, az ABCD négyszög deltoid, BD felezi mind az ADC, mind pedig az ABC szöget. Ezt viszont a feltétel kizárja, az adott feltételek esetén tehát ABCD valóban húrnégyszög.
 
6. Egy pozitív egész számot alternálónak nevezünk, ha a tízes számrendszerbeli felírásában a szomszédos számjegyek mindig különböző paritásúak.
Határozzuk meg az összes olyan n pozitív egész számot, amire igaz az, hogy n-nek van olyan többszöröse, ami alternáló szám.
 
 

Pach Péter Pál megoldása. Ha 20∣n, akkor az n utolsó jegye 0 és 4∣n miatt az utolsó előtti jegy páros, így ekkor az n-nek nincsen alternáló többszöröse. A továbbiakban több lépésben igazoljuk, hogy a 20∤n feltétel elégséges, ebben az esetben létezik olyan alternáló szám, amelyik osztható n-nel.
 
a) Legyen először n=2k. Megmutatjuk, hogy létezik olyan alternáló számokból álló A1,A2,...,Ak,... sorozat, amelyben Ak-nak k jegye van (k=1,2,...), Ak+1 az Ak ,,folytatása'', tehát első jegyét elhagyva Ak-t kapjuk, 2k∣Ak, továbbá 2k+1∣Ak pontosan akkor teljesül, ha k páros. Az Ak sorozatot teljes indukcióval állítjuk elő: k=1, illetve k=2 esetén A1=2 és A2=32 megfelelő.
Legyen k≥2 páros és tegyük fel, hogy az Ak számot már megadtuk a feltételeknek megfelelően, tehát Ak  k-jegyű alternáló szám és osztható 2k+1-nel. Mivel k páros, Ak első jegye páratlan. Így akár 2-est, akár 4-est írunk a szám elejére, (k+1)-jegyű alternáló számot kapunk és 2k+1∣2⋅10k, illetve 2k+1∣Ak miatt mindkét esetben 2k+1 többszörösét kapjuk. Mivel k+1 páratlan, meg kell még mutatnunk, hogy 2⋅10k+Ak és 4⋅10k+Ak valamelyike nem osztható 2k+2-nel. Ez nyilvánvaló, ellenkező esetben ugyanis a különbségük, 2⋅10k=2k+1⋅5k is osztható volna 2k+2-nel. Így ha k páros, akkor létezik a megfelelő Ak+1.
Legyen most a k páratlan. Ekkor Ak első jegye páros, így 1-et, illetve 3-at írva a szám elejére (k+1)-jegyű alternáló számot kapunk. A konstrukció szerint 2k∣Ak és 2k+1∤Ak, így Ak≡2k(mod2k+1), továbbá nyilván 1⋅10k≡3⋅10k≡2k(mod2k+1). A megfelelő kongruenciákat összeadva kapjuk, hogy mindkét így adódó szám osztható 2k+1-nel. Mivel a különbségükben, 2⋅10k=2k+1⋅5k-ban is k+1 a 2 kitevője, azért legalább az egyikük még 2k+2-nel is osztható. Így az Ak+1=10k+Ak vagy Ak+1=3⋅10k+Ak választás megfelelő.
b) Ha n=5k, akkor ismét indukcióval megmutatjuk, hogy az n-nek van legfeljebb k-jegyű Bk alternáló többszöröse. (Bk legelső jegye lehet 0 is.)
Ha k=1, akkor B1=5 megfelelő. Legyen k≥1 és a Bk olyan, legfeljebb k-jegyű alternáló szám, amelyre Bk≡0(mod5k). Ekkor valamilyen i∈{0;1;2;3;4} számra Bk≡i⋅5k(mod5k+1). Ha Bk elejére egy újabb x számjegyet akarunk betoldani, akkor az oszthatósághoz
x⋅10k+Bk≡0(mod5k+1),azazx⋅10k+i⋅5k=5k(x⋅2k+i)≡0(mod5k+1)
szükséges. Ez pontosan akkor teljesül, ha x⋅2k+i≡0(mod5). Mivel (2k;5)=1, azért ennek a kongruenciának van megoldása mod 5. Végül vegyük észre, hogy az x paritását megválaszthatjuk, hiszen a páros, illetve a páratlan számjegyek is egy-egy teljes maradékrendszert alkotnak (mod 5). Így a megfelelő választással Bk+1=x⋅10k+Bk is alternáló szám lesz, amely osztható 5k+1-nel.
c) Ha (10;n)=1, akkor a feladat állításán túlmenően azt igazoljuk, hogy az x≡r(modn) kongruenciának minden r maradék esetén létezik adott paritású alternáló megoldása.
Először azt mutatjuk meg, hogy ha (10;n)=1, akkor van olyan teljes maradékrendszer (mod n), amelynek az elemei csak a 2 és a 0 számjegyeket tartalmazzák.
Az Euler‐Fermat-tétel szerint ugyanis 10φ(n)≡1(modn), így ha k1,k2,...,kr különböző pozitív egészek, akkor
Tr=10k1φ(n)+10k2φ(n)+...+10krφ(n)≡1+1+...+1︸r≡r(modn),
a Tr számokból tehát teljes maradékrendszer készíthető (mod n). Mivel (2;n)=1, azért a 2Tr számok is teljes maradékrendszert alkotnak (mod n) és rendelkeznek az előírt tulajdonsággal.
Tekintsünk most egy olyan H=1010...10 alakú alternáló számot, amely a fenti 2Tr alakú számokból álló teljes maradékrendszer minden eleménél több jegyből áll. Ekkor az A+2Tr alakú számok is teljes maradékrendszert alkotnak (mod n), másrészt maguk is alternálók, hiszen a H alternáló számhoz olyan ,,rövidebb'' számokat adtunk, amelyek minden jegye páros és a jegyek kicsik, tehát nincs tízes átlépés. Ebben az alternáló teljes maradékrendszerben minden szám páros.
Ha most a
10H+1=1010...10︸H1
páratlan alternáló számhoz adjuk hozzá a teljes maradékrendszer 2Tr elemeit, akkor alternáló páratlan számokból álló teljes maradékrendszert kapunk (mod n).
Ebből következik, hogy ha (10;n)=1, akkor n-nek van alternáló többszöröse, az erősebb állításra a későbbiekben lesz szükség.
d) Hátra van még az az eset, amikor n osztható 2-vel vagy 5-tel, de nem osztható 20-szal. Ha n=2α⋅5β⋅n1, ahol (n1;10)=1, akkor vagy α≤1 és β>0, vagy pedig α≥1 és β=0. Ha α≤1 és β>0, akkor b) szerint 5β-1-nek létezik legfeljebb (β-1)-jegyű B alternáló többszöröse, amelynek utolsó jegye, 5, páratlan. Így B1=10B  β-jegyű alternáló szám és α≤1 miatt 2α⋅5β∣B1.
Olyan C alternáló számot keresünk, amelyre D1=C⋅10β+B1 is alternáló és osztható n-nel. Mivel 2α⋅5β∣10β, azért 2α⋅5β∣D1. Most (10;n1)=1, tehát c) szerint az x⋅10β+B1≡0(modn1) kongruenciának létezik adott paritású alternáló megoldása, így B1 első jegyének paritásától függően olyan is, amelyre D1 is alternáló. Miután most (n1;2)=(n1;5)=1, azért n=2α⋅5β⋅n1∣D1.
Végül ha β=0 és α≥1, akkor ugyanígy okoskodhatunk. a) szerint van olyan α-jegyű A alternáló szám, amelyre 2α∣A, c) szerint pedig a 10α⋅x+A≡0(modn1) kongruenciának van adott paritású alternáló megoldása. Ekkor 2α∣10α, tehát 2α∣10α⋅x+A, (2;n1)=1 miatt n=2α⋅n1∣10α⋅x+A és x paritását az A első jegyével ellentétesnek választva 10α⋅x+A is alternáló szám lesz.
Ezzel minden esetet megvizsgáltunk, a bizonyítást befejeztük.
*Ennek bizonyítását az értékelés során nem várták el a versenyzőktől; maga a bizonyítás nem nehéz, inkább technikai jellegű.