|
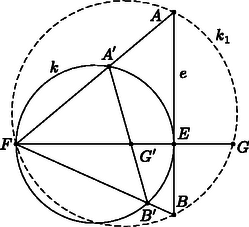
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. feladat. Az átmérőjű kört az egyenes az pontban érinti. Tekintsük az egyenes összes olyan , pontpárját, melyre az szakasz az pontot tartalmazza és egy rögzített állandó. Egy ilyen pontpár esetén legyen , illetve a kör metszéspontja az , illetve szakasszal. Igazoljuk, hogy az szakaszok egy ponton mennek keresztül.
I. megoldás. Legyen az háromszög köré írt kör és az egyenes -től különböző metszéspontja . Az pontnak körre vonatkozó hatványa állandó, ezért a pont helyzete nem függ az , pontpár megválasztásától.
Tekintsük most azt az inverziót, amelynek alapköre az középpontú, sugarú kör. Az egyenes inverze a kör, az és pontok inverze az , illetve a pont. A kör inverze az egyenes; ezen belül is a -t tartalmazó körív képe az szakasz. Az szakasz tehát mindig átmegy a pont inverzén, -n, mely, mint azt láttuk, független az és pontok választásától.
Megjegyzések. 1. A fenti megoldás az inverzió tulajdonságaira épít, amely nem feltétlenül tananyag a középiskolában (lásd hátsó belső borítóoldalt). Ugyancsak inverziót használ megoldásában Balogh László és Maga Péter.
2. A fenti megoldásból könnyen látható, hogy ha , akkor
A továbbiakban megadunk két, szokásosabb megoldást is.
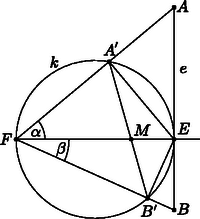
II. megoldás. Legyen most és metszéspontja . Megmutatjuk, hogy minden , pár esetén ugyanaz a pont; másképpen, az hossza állandó. Az hosszát az háromszög és négyszög területének arányával fogjuk kifejezni: Válasszuk az szakasz hosszát egységnek, legyen és . Az érintő tulajdonság és a Thalész-tétel szerint az , , illetve és háromszögek derékszögűek, így , , , , és . A keresett területek tehát:
Végül
Az szakasz hossza tehát állandó.
III. megoldásvázlat (Kis Gergely megoldása). Válasszuk középpontját az origónak, sugarát egységnyinek, legyenek továbbá az és pontok koordinátái rendre , ill. . Az és egyenesek, ill. a kör egyenletei rendre
A megfelelő egyenletpárok megoldásából a metszéspontokra | |
adódik. Az egyenes egyenlete innen | |
Az egyenes tengellyel való metszéspontjának koordinátája a fenti egyenletből helyettesítéssel Ez a mennyiség állandó, hiszen állandó. Ez azt jelenti, hogy az egyenesek mindegyike átmegy az ponton.
2. feladat. Egy gráf -színezése a csúcsainak megszínezése lehetséges szín felhasználásával úgy, hogy bármely élének végpontjai különböző színűek legyenek. Azt mondjuk, hogy egyértelműen -színezhető, ha egyrészt -nek létezik -színezése, másrészt nem léteznek -nek olyan és csúcsai, melyek valamely -színezésében azonos színűek, míg egy másik -színezésében egymástól különböző színt kapnak.
Bizonyítsuk be, hogy ha az pontú gráf egyértelműen -színezhető és , akkor -nek legalább éle van.
Megoldás. Rögzítsük egy -színezését, melyben az egyes színekre színezett csúcsok száma (azaz a színosztályok mérete) , , illetve . Világos, hogy .
Tegyük fel, hogy két színosztály (mondjuk a piros és a zöld) nem feszít -ben összefüggő gráfot, azaz a piros és zöld csúcsok között futó élek alkotta részgráfnak legalább két komponense van. Amennyiben e komponensek valamelyikén a színeket felcseréljük (vagyis ezen a komponensen belül a korábban zöld csúcsok pirosak lesznek, a pirosak pedig zöldek), úgy továbbra is igaz marad, hogy bármely élének végpontjai különböző színűek. A cserével tehát egy olyan -színezéséhez jutunk, melynek színosztályai másképpen osztják három csoportra csúcsait, mint az eredeti színezés színosztályai. Ezért az új -színezésben vagy két, korábban azonos színű pont különböző színt kapott, vagy két, korábban különböző színű pont azonos színű lett, esetleg mindkét változásra sor kerülhetett. Ez ellentmond annak, hogy egyértelműen színezhető 3 színnel, vagyis bármely két színosztálya összefüggő gráfot feszít.
Ismert, hogy egy összefügő gráf élszáma legfeljebb -gyel kevesebb, mint pontjainak száma, ezért az első két színosztály legalább , a második és harmadik színosztály legalább , míg az első és harmadik színosztály legalább különböző élt tartalmaz. Az említett élek egymástól is különböznek, ezért élszámára az alsó becslést kapjuk.
Megjegyzések. 1. Többen próbálták a feladatot teljes indukcióval megoldani: az állítás -pontú gráfokra világos, tegyük fel, hogy a legfeljebb -pontú gráfokra már bizonyítottuk a becslést. Ha az -pontú, egyértelműen -színezhető gráfnak minden csúcsa legalább -edfokú, akkor élszáma legalább , így az állítás igaz. Ha van -nek másodfokú csúcsa, akkor annak törlésével (mint az könnyen látható) egy egyértelműen -színezhető gráf keletkezik, melyre igaz az indukciós feltevés: legalább éle van, ezért élszáma nem kevesebb, mint . Az elintézetlen eset az, amikor -ben a minimális fokszám . Sajnos, ha egy harmadfokú csúcsát elhagyjuk, a maradék gráf nem lesz feltétlenül egyértelműen -színezhető: elképzelhető ugyanis -nek olyan -színezése, melyben szomszédai különböző színeket kapnak. Ha ezt követően pl. összehúzzuk két azonos színű szomszédját, akkor a kapott gráf már egyértelműen -színezhető, azonban csupán -mal kevesebb éle van, mint -nek. Az indukciós bizonyításhoz pedig legalább -gyel kevesebb élre volna szükség.
A bizottság nem ismer a fenti gondolatmenetet teljes indukciós bizonyítássá kiegészítő érvelést.
2. Többen igazolták, hogy a feladatban adott korlát elérhető. Világos, hogy a -pontú teljes gráf egyértelműen -színezhető, és éle van. Az is könnyen látszik, hogy ha egy egyértelműen -színezhető gráfhoz hozzáveszünk egy új pontot, melyet két különböző színű pontjával kötünk össze, akkor újabb egyértelműen -színezhető gráfot kapunk, melyre a becslés pontos lesz, ha már -re is az volt.
3. A feladat megoldása értelemszerű módosításokkal kiterjeszthető egyértelműen -színezhető gráfok élszámának becslésére is, azaz megmutatható, hogy tetszőleges egyértelműen -színezhető gráfnak legalább éle van. A 2. megjegyzés is kiterjeszthető: a -pontú teljes gráf egyértelműen -színezhető, és egy egyértelműen -színezhető gráfhoz új pontot hozzávéve és különböző színű ponttal összekötve ismét egyértelműen -színezhető gráfot kapunk.
4. Akkor is alkalmazható a módszerünk, ha nem az egyértelműen -színezhető gráfok élszámát akarjuk megbecsülni, hanem csupán felső korlátunk van -színezéseinek számára. A megoldás gondolatmenetével felső becslést kaphatunk két színosztály által feszített komponensek számára, innen pedig a két komponens által feszített élek száma alulról becsülhető.
3. feladat. Jelölje az és egész számok legnagyobb közös osztóját. Bizonyítsuk be, hogy véges sok kivételtől eltekintve minden pozitív egész számra teljesül a egyenlőtlenség.
I. megoldás. Vizsgáljuk meg, hogy egy rögzített szám hányszor lép fel -ként a feladatbeli összegben! Világos, hogy ha , akkor és relatív prímek, továbbá mindkettő az intervallumba esik, ahol az alsó egészrészét jelöli.
Másfelől, ha relatív prímek, akkor , ill. esetén és . A feladatbeli egyenlőtlenség bal oldalán álló mennyiséget -nel jelölve, a fenti gondolatmenet formálisan az alábbi összeg átrendezése: | | (1) |
ahol az és közé eső számokból alkotható relatív prím számpárok száma. A továbbiakban értékét fogjuk megbecsülni, pontosabban igazoljuk, hogy Mivel az számpár megfelelő, ezért esetén triviálisan teljesül. A becslés úgy adódik, hogy az összes számpárok számából minden -re kivonjuk azon számpárok számát, melyeknek közös osztója. Azaz,
A becslést (1)-be helyettesítve azt kapjuk, hogy | | (3) |
Ismert, hogy a harmonikus sor divergens, ezért valamely -re teljesül (például megfelel), így -re (3) alapján | |
amint azt bizonyítanunk kellett.
Megjegyzések. 1. A bizonyításból látható, hogy a feladatbeli becslés jobb oldalán álló -es szorzó tetszőleges konstanssal helyettesíthető azon az áron, hogy megnő az a legnagyobb egész, melyre a feladatbeli egyenlőtlenség még nem teljesül.
2. Mélyebb számelméleti ismereteket felhasználva megmutatható, hogy a megoldásban szereplő függvény aszimptotikusan , ahonnan a feladatban szereplő összeg értéke aszimptotikusan -nek adódik.
3. A legtöbb megoldó a fentinél kevésbé elemi, a prímek reciprokösszegének divergenciájára építő megoldást talált. Az alábbiakban vázoljuk ezt a gondolatmenetet.
II. megoldás. Az legnagyobb közös osztót az , számok közös prímosztóinak összegével becsüljük. Legyenek mindazon prímek, melyek az és számokat egyaránt osztják. Mivel bármely szóban forgó prím legalább , ezért
teljesül. Jól ismert, hogy a prímek reciprokösszege -hez tart, így létezik olyan szám, melyre az és közti prímek reciprokösszege nagyobb, mint . Ha tehát , akkor (4) alapján az I. megoldásban definiált -t az alábbi módon becsülhetjük:
|
 PDF | MathML
PDF | MathML