Kezdőlap


Cím:	Kiegészítések az Eötvös-verseny 2. feladatának megoldásához
Szerző(k):	Gnädig Péter
Füzet:	2004/március, 177 - 180. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Sokféle út vezet az ,,üdvösséghez''; a fizikai problémák megoldásához is ‐ számos esetben ‐ többféle gondolatmenettel el lehet jutni. Jó példa erre a 2003. évi Eötvös-verseny 2. feladata, amely lapunk 171. oldalán olvasható megoldása mellett más módszerekkel is kezelhető. Ezen ,,alternatív'' gondolatmenetek közül ismertetünk most kettőt. Mindkettő a versenydolgozatokban bukkant fel (részben vagy teljesen kidolgozva), és a megoldások szépsége (eleganciája) miatt feltétlenül megérdemlik, hogy Olvasóink is megismerkedjenek velük.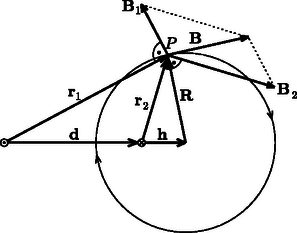

I. megoldás (Csóka Endre dolgozata alapján). Bebizonyítjuk, hogy a mágneses indukcióvonalak (az áramvezetők közti távolságot felező ponton áthaladó egyenestől eltekintve) körök.

1. ábra

Tekintsük az áramvezetőkre merőleges síkmetszetet, és használjuk az 1. ábrán látható vektor-jelöléseket! (A vektorokat a továbbiakban vastag betűvel jelöljük, az abszolút értéküket pedig a megfelelő betű vastagítás nélküli párjával; pl.

| B | = B

.) Az egyes áramvezetők által létrehozott mágneses indukcióvektor tetszőleges helyen, így a

P

pontban is merőleges a vezetőtől a kérdéses pontba mutató

r

vektorra, és a nagysága ‐ a gerjesztési törvény értelmében ‐ a távolsággal fordítottan arányos:

\begin{matrix} B_{1} ⊥ r_{1}, illetve B_{2} ⊥ r_{2}, \end{matrix}

továbbá

\begin{matrix} B_{1} = \frac{K}{r_{1}}, és B_{2} = \frac{K}{r_{2}}, \end{matrix}

ahol

K

egy ‐ számunkra érdektelen ‐ állandó.
Azt szeretnénk belátni, hogy az eredő mágneses indukció,

B_{1}

iránya egy alkalmasan választott kör

R

rádiusz-vektorára merőleges, tehát a kör érintőjével párhuzamos. Forgassuk el gondolatban

90

fokkal a

B_{1}

és

B_{2}

vektorokat, és velük együtt az eredő

B

vektort is; legyenek az elforgatott vektorok

B_{1}^{*}

B_{2}^{*}

és

B^{*}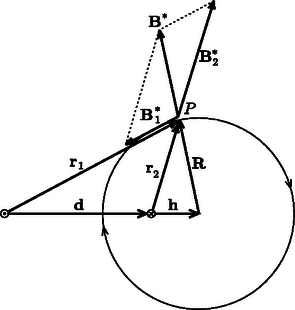

(2. ábra).

2. ábra

B_{1}^{*}

vektor ellentétes irányú az

r_{1} = d + h + R

vektorral,

B_{2}^{*}

pedig egyállású az

r_{2} = h + R

vektorral, tehát az eredőjük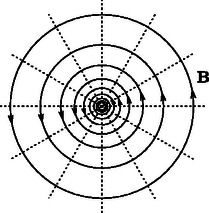

\begin{matrix} B^{*} = B_{1}^{*} + B_{2}^{*} = - \frac{K}{r_{1}^{2}} (d + h + R) + \frac{K}{r_{2}^{2}} (h + R) . \end{matrix}

Ez a vektor akkor lesz a

P

pont helyzetétől, vagyis az

R

vektor irányától függetlenül

R

-rel párhuzamos, ha

\begin{matrix} \frac{1}{r_{1}^{2}} (d + h) = \frac{1}{r_{2}^{2}} h, \end{matrix}

azaz (

d

és

h

azonos irányát is figyelembe véve) fennáll, hogy

\begin{matrix} λ = \frac{r_{2}}{r_{1}} = \sqrt[]{\frac{h}{d + h}} = állandó . \end{matrix}

Ez pedig nem más, mint az Apollóniosz-körök jellemzője.

II. megoldás (Balogh László sejtése alapján). Tekintsünk először egyetlen hosszú, egyenes áramjárta vezetőt, melynek mágneses erővonalai a vezetőt körülölelő koncentrikus körök (3. ábra). Az ábrán az erővonalak sűrűségét a térerősség nagyságával arányosan választottuk meg, és szaggatott vonalakkal bejelöltünk egy ‐ az erővonalakra merőleges ‐ egyenes-sereget is. Ez utóbbiak ‐ az elektrosztatikus mező potenciálfelületeihez hasonlóan ‐ a ,,síkbeli'' magnetosztatikus mező ekvipotenciális vonalaiként is felfoghatók.

3. ábra

Az ábrán látható két vonalsereget figyelve feltűnhet a hasonlóság egy alkalmasan választott elektrosztatikai problémával. Egy hosszú, egyenes, egyenletesen feltöltött szál elektromos erővonalrendszere és az ekvipotenciális görbéi (a szálra merőleges síkban) éppen úgy néznek ki, mint a vizsgált mágneses mező (4. ábra), csak éppen a szerepek cserélődnek fel: a mágneses tér erővonalai az elektrosztatikus mező potenciálvonalainak, a mágneses erővonalakra merőleges ,,mágneses potenciálvonalak'' pedig az elektromos tér erővonalainak felelnek meg. (Még a mágneses erővonalak sűrűsége is éppen úgy függ az áramvezetőtől mért távolságtól, mint ahogy az elektrosztatikus problémánál a potenciálgörbék sűrűsége: mindkettő a távolság reciprokával arányos.)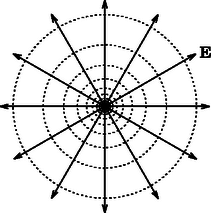

4. ábra

Felmerül a kérdés, hogy ez az analógia más, kissé bonyolultabb, még mindig vákuumbeli, de továbbra is síkbeli elektrosztatikus és magnetosztatikus mezők között is fennáll-e. (Síkbelinek nevezünk egy

v (r)

vektormezőt, ha csak 2 komponense különbözik nullától, és ezek csak két koordinátától függnek; pl.

v_{x} (x; y)

és

v_{y} (x; y)

. A ponttöltés elektrosztatikus tere nem síkbeli, de egy hosszú egyenes vezetőé már az.) Ha igen, akkor érdemes a mágneses erővonalak (egy vektormező irányát és nagyságát megadó görbék) helyett a megfelelő elektrosztatikus potenciált (tehát egy skalár mennyiséget) kiszámítani, és megvizsgálni, hogy milyen görbék mentén állandó ez a potenciálfüggvény.
Az 5. ábra alapján könnyen beláthatjuk, hogy az említett kettősség valóban fennáll. Az

(a)

ábrán a

Φ

-vel jelölt vonalak az (elektromos) ekvipotenciális vonalak,

Ψ

pedig az elektromos tér erővonalait sorszámozza. Tekintsük a besatírozott kicsiny területet, amely

a

és

b

oldalélű téglalappal közelíthető. Az elektromos térerősség nagysága kétféle módon is kiszámítható: egyrészt az erővonalak sűrűségeként (ami jelen esetben az egységnyi hosszra jutó erővonalak száma), másrészt úgy, mint az elektrosztatikus potenciál egységnyi hosszra eső megváltozása, azaz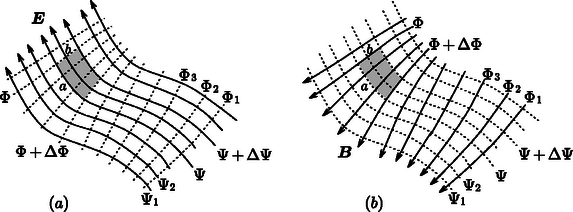

\begin{matrix} | E | = \frac{Δ Ψ}{b} = \frac{Δ Φ}{a} . \end{matrix}

5. ábra

(b)

ábrán látható mágneses tér szempontjából viszont azt írhatjuk fel, hogy

\begin{matrix} | B | = \frac{Δ Φ}{a} = \frac{Δ Ψ}{b} . \end{matrix}

Látható, hogy a két formula ugyanazt a megszorítást rója ki

Ψ

és

Φ

egységnyi hosszra eső változási ütemére, tehát ha ez a feltétel teljesül, akkor abból akár

E

, akár pedig

B

meghatározható.
Alkalmazzuk a kapottakat az eredeti problémára, a párhuzamos egyenes vezetők mágneses terére, illetve a megfelelő elektrosztatikus problémára, a párhuzamos, hosszegységenként azonos nagyságú, de ellentétes előjelű töltéssel rendelkező szálakra. Egyetlen töltött szál elektromos tere a száltól mért távolsággal fordítottan arányos:

\begin{matrix} E (r) = \frac{K}{r}, \end{matrix}

ahol

K

a szál töltésével arányos állandó. Az elektrosztatikus potenciál azzal a munkával egyenlő, amelyet akkor végzünk, amikor egységnyi töltés távolságát a száltól a potenciál nullpontjának választott

r_{0}

-nak megfelelő értékről

r

-re változtatjuk:

\begin{matrix} Φ (r) = - K \int_{r_{0}}^{r} \frac{1}{r} d r = - K ln \frac{r}{r_{0}} . \end{matrix}

A két ellentétesen feltöltött szál együttes potenciálja

\begin{matrix} Φ (r) = Φ_{1} (r) + Φ_{2} (r) = K ln \frac{r_{1}}{r_{0}} - K ln \frac{r_{2}}{r_{0}} = K ln \frac{r_{1}}{r_{2}} . \end{matrix}

Ez a kifejezés akkor állandó, ha a szálaktól mért távolságok aránya állandó, vagyis ha rajta vagyunk valamelyik Apollóniosz-körön. Ezek a körök alkotják tehát az eredeti feladatban a mágneses mező erővonalait.
A fenti gondolatmenetből látszik, hogy a különböző erősségű áramokkal átjárt vezetők mágneses erővonalai az

\begin{matrix} {(r_{1})}^{n} \cdot r_{2} = állandó \end{matrix}

egyenlettel írhatók le, ahol

n

a vezetékekben folyó áramok erősségének aránya. (Az Eötvös-versenyen szereplő feladatban

n = - 1

. Ha például azonos nagyságú és megegyező irányú áramok eredő mágneses terére vagyunk kiváncsiak, az erővonalak az

r_{1} r_{2} = állandó

egyenlettel jellemzett görbék, az ún. lemniszkáták.)
Hangsúlyoznunk kell, hogy a sztatikus elektromos és mágneses mezők közötti hasonlóság csak síkbeli problémáknál, tehát két dimenzióban áll fenn. A háromdimenziós térben az ekvipotenciális pontok felületet alkotnak, míg az erővonalak továbbra is görbék, tehát egydimenziós alakzatok, így az egyik erőtér ,,potenciál-térképe'' biztosan nem feleltethető meg a másik erőtér erővonalainak. Azt is meg kell említenünk, hogy a ,,mágneses potenciálfüggvény'' a szokásos matematikai függvényfogalomtól eltérően ,,többértékű''; ha az áramvezetőt körbejárjuk, a potenciálfüggvény értéke nem lesz ugyanannyi a végpontban, mint a kezdőpontban. (Végtelen egyenes vezetőnél pl. a mágneses potenciál az azimutszöggel arányos.) Emiatt a mágneses indukció általában nem konzervatív vektormező.