Kezdőlap


Cím:	A munkára fogott véletlen II. rész
Szerző(k):	Cserti József
Füzet:	2003/november, 493 - 497. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Fizikai alkalmazások

Cikkünk első részében bemutattuk a Monte-Carlo-módszer alapjait és néhány egyszerű matematikai alkalmazását. Ezt az eljárást ‐ többek között ‐ a fizikusok is nagyon sok területen használják. A számos fizikai alkalmazás közül a továbbiakban két példát fogunk bemutatni.

Súlypont meghatározása. A középiskolás függvénytáblázatban megtalálható a súlypont meghatározásának módja, és néhány speciális alakzatra zárt alakban megadható képleteket is felírhatunk. (Például egy

r

sugarú, homogén tömegeloszlású félkör alakú lap súlypontja a középponttól

\frac{4 r}{3 π}

távol van.) Bonyolultabb alakzatokra már igen nehéz kiszámítani a súlypont helyét, az általában csak integrálszámítással határozható meg.
Tekintsük például az I. rész 4. ábráján látható, kalapfüggvénynek nevezett alakzatot. Az egyszerűség kedvéért most csak olyan síkbeli alakzatokat vizsgálunk, amelyeknek van szimmetriatengelye. A kalapfüggvény szimmetriatengelye az

[a, b] = [0, π]

intervallumon az

x = π / 2

függőleges egyenes, így nyilvánvaló, hogy a súlypont vízszintes koordinátája

π / 2

. A függőleges koordinátát azonban már nem tudjuk elemi úton kiszámítani.
Az általános módszer szerint felosztjuk az alakzatot sok kicsi részre, melyek tömege

m_{i}

, és elegendően finom felosztás esetén a súlypont függőleges helyét a következő képlettel számíthatjuk ki:

\begin{matrix} y_{s} = \frac{\sum_{i}^{} y_{i} m_{i}}{\sum_{i}^{} m_{i}} . \end{matrix}

A nevező arányos az alakzat területével. Cikkünk I. részében Monte-Carlo-módszer segítségével már kiszámítottuk a kalapfüggvény területét:

A \approx 1, 219

. A fenti képlet számlálóját is kiszámíthatjuk a Monte-Carlo-módszerrel. Generáljunk egy

x

és egy

y

véletlen számot a

[0,1]

intervallumban. Az

x \to x π

és

y \to M y

transzformációval az

(x, y)

koordinátájú pont a

π

és

M

oldalhosszúságú téglalapba fog esni (

M

a kalapfüggvény maximuma:

M = sin^{2} (1) = 0, 7081

). Ekkor a következő igen egyszerű algoritmussal számíthatjuk ki a fenti képlet számlálóját:


if (y < f(x) ) then
    S = S + y
    N_be = N_be + 1
endif

Az algoritmust

N_{össz}

alkalommal végrehajtva a fenti képlet számlálóját az

S M π / N_{össz}

értékkel közelíthetjük. Itt

N_{be}

azoknak az

(x, y)

pontoknak a számát jelöli, amelyek az

f (x)

alá esnek. Cikkünk I. részében láttuk, hogy a görbe alatti területet közelítőleg az

A = M π N_{be} / N_{össz}

kifejezés alapján határozhatjuk meg. Így a súlypont függőleges koordinátáját az

\begin{matrix} y_{s} = \frac{S}{N_{be}} \end{matrix}

képletből számíthatjuk ki. Ne felejtsük el az

S

és

N_{be}

változókat nullázni a ciklus elején! Természetesen a fenti programrészletet a használt programnyelv szabályai szerint esetleg át kell írni. Érdemes megjegyezni, hogy a súlypontnak a Monte-Carlo-módszerrel történő kiszámításához nem volt szükség a görbe alatti területre.

1. ábra. A kalapfüggvény súlypontja Monte-Carlo-módszer alapján. A szaggatott vonal az egzakt értéket jelzi

Integrálszámítással a súlypontra a pontosnak mondható

y_{s} = 0, 274 975

értéket kapjuk. Az 1. ábrán a súlypontnak különböző számú kísérletekből kapott értékeit ábrázoltuk, és feltüntettük az egzakt értéket is (szaggatott vonal). Látható, hogy

N_{össz} = 10^{6}

kísérlet esetén már nagyon jól egyezik a ,,mérésünk'' a pontos értékkel (0,02%-os az eltérés).

Ising-modell. Egyes anyagok mágneses tulajdonságokkal rendelkeznek. Már az ókori görögök ismerték azokat a Magnezia környékén található ,,köveket'', melyek vonzzák a vasat. Egészen a XX. századig, a kvantummechanika törvényeinek felismeréséig nem sikerült kielégítően magyarázni az anyagok mágneses viselkedését. Az Ising által kidolgozott modell fontos előrelépést jelentett ebben a kutatásban. Ezen egyszerűsített modell szerint az anyagban lévő kis mágnesek (mai ismereteink szerint az atomok spinjei) két állapot valamelyikében lehetnek: vagy azonos, vagy ellentétes irányban állnak a külső mágneses térhez képest.
Képzeljük el, hogy a kis mágnesek egy négyzetrács pontjaiban helyezkednek el. Feltesszük, hogy a négyzetrács

i

-edik rácspontjában egy kis mágnes (spin) van, melynek értéke

S_{i} = \pm 1

, attól függően, hogy a spin azonos vagy ellentétes irányú a külső

H

térrel:

\begin{matrix} S_{i} = {\begin{matrix} 1, & ha ↑ \\ - 1, & ha ↓ . \end{matrix} \end{matrix}

A spinek egyik lehetséges beállása látható a 2. ábrán. Az egyes mágnesek ,,érzik'' a többi mágnes pillanatnyi irányát, más szóval a spinek kölcsönhatnak egymással. A modellben csak a közvetlen szomszédok (ún. elsőszomszédok) közti kölcsönhatást vesszük figyelembe, a távolabbi mágnesek egymásra hatásait elhanyagoljuk. Így minden rácspontban a spin a 4 elsőszomszédjával hat csak kölcsön. A külső

H

mágneses tér igyekszik a spineket a tér irányába állítani. A fenti kölcsönhatások alapján a rendszer teljes

E

energiáját a következő alakban írhatjuk fel:

\begin{matrix} E = - J \sum_{〈 i, j 〉}^{} S_{i} S_{j} - H \sum_{i}^{} S_{i}, \end{matrix}

ahol

J

a szomszédos spinek közti kölcsönhatás erősségére jellemző szám, melyet csatolási állandónak szoktak nevezni. Az első tagban az összegzést csak az elsőszomszédokra vesszük, erre utal a

〈, 〉

jelölés.

2. ábra. A spinrendszerek Ising-modellje. A külső

H

mágneses térhez képest a spinek vagy azonos, vagy ellentétes irányban állnak

A rendszer

M

mágnesezettsége az összes spinváltozó összege (vagy ezzel az összeggel arányos):

\begin{matrix} M = \sum_{i}^{} S_{i} . \end{matrix}

Hűtsük le a rendszert (gondolatban) abszolút zérus fokra, és fokozatosan kapcsoljuk ki a külső mágneses teret is! Ekkor a rendszer alapállapotba (a legalacsonyabb energiájú, másszóval energetikailag ,,legkedvezőbb'' állapotba) kerül. Ha a

J

csatolási állandó pozitív, akkor energetikailag az a kedvező állapot, ha minden spin azonos irányba áll (hiszen ebben az esetben a szomszédos spinek szorzata

+ 1

), tehát egy rendezett állapot alakul ki. Alapállapotban és

J > 0

esetén a rendszer mágnesezettsége maximális. Ezt az anyag erősen mágneses, ferromágneses állapotának nevezik.
A hőmérséklet növelésével egyes spinek ,,átbillennek'' az ellentétes irányú állapotba, és így lecsökken a rendszer mágnesezettsége. Egy bizonyos

T_{c}

hőmérsékletérték után ‐ külső mágneses tér nélkül ‐ átlagosan a spinek fele felfelé, másik fele lefelé áll: a rendszer

M

mágnezettsége zérus lesz. Ezt a hőmérsékletet kritikus hőmérsékletnek nevezik, és Pierre Curie francia fizikus kutatásai nyomán Curie-hőmérsékletnek is hívják. A hőmérséklet teljesen ,,szétzilálja'' a rendezett állapotot még zérus

H

tér mellett is.

T_{c}

alatt a rendszer mágnesezettsége véges értékű, míg

T_{c}

fölött zérus. Ez a jelenség (a sok tekintetben hasonló halmazállapotváltozásokkal együtt) a fázisátalakulások családjához tartozik. Ezen egyszerű modell alapján is megérthetjük fizikailag, hogy miért veszti el egy mágnes a mágnesességét, ha tűzbe dobjuk. A mágnesezettség hőmérsékletfüggését (vázlatosan) a 3. ábra mutatja.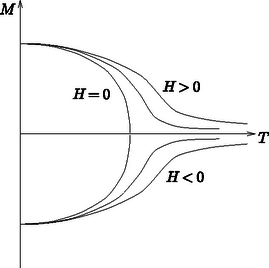

3. ábra. Ising-modell mágnesezettségének hőmérséklettől való függése különböző külső mágneses terek esetén

Érdemes megjegyezni, hogy ha a

J

csatolási állandó negatív, akkor alapállapotban és

H = 0

esetén a szomszédos spinek ellentétes irányban állnak (ekkor két szomszédos spin szorzata

- 1

), más szóval egy ,,sakktáblaszerű'' állapot alakul ki. Az ilyen (a természetben is megfigyelhető) rendszereket antiferromágneseknek nevezik.
Továbbiakban egy, a Monte-Carlo-módszeren alapuló algoritmust mutatunk be, mellyel meghatározhatjuk a 3. ábrán látható mágnesezettségnek hőmérséklettől és a külső mágneses tértől való függését. Az algoritmust először N. Metropolis görög származású amerikai matematikus alkalmazta spinrendszerekre a múlt század közepén, és azóta Metropolis-algoritmusnak is nevezik [1]. A spineket gondolatban egy négyzetrácsra helyezzük a 2. ábrának megfelelően, és periodikus határfeltételt alkalmazunk. Ez azt jelenti, hogy a teljes négyzetrácsot periodikusan ismétlődőnek képzeljük a négyzet oldaléleinek irányában, vagy ami ezzel egyenértékű: a négyzetrácsot egy tóruszra (kerékpárbelső alakú felületre) rajzoljuk. Ezzel a ,,trükkel'' azt érjük el, hogy az eredeti négyzet szélein lévő spineknek is négy elsőszomszédja legyen, tehát egyenértékűek legyenek a rács belsejében található társaikkal.
Induljunk ki a spinek valamilyen kezdeti elrendeződéséből (konfigurációjából)! Választhatjuk pl. a zérus hőmérsékletnek megfelelő rendezett állapotot, az alapállapotot kiindulási konfigurációként. Ezután a következő lépéseket ismételjük:

1.	Véletlenszerűen kiválasztunk egy spint. Kiszámítjuk, hogy az átfordításával mennyit változna meg a rendszer energiája. Legyen ez az energiaváltozás $Δ E$ .

Kiszámoljuk annak valószínűségét, hogy

T

hőmérsékleten a kiválasztott spin átfordul az ellentétes irányú állapotba. Ez a valószínűség (az ún. átmeneti valószínűség) az alábbi képlettel adható meg:

\begin{matrix} W = {\begin{matrix} 1, & ha Δ E < 0 \\ e^{\frac{Δ E}{k T}}, & ha Δ E > 0, \end{matrix} \end{matrix}

ahol

k

a Boltzmann-állandót jelöli.

3.	Generálunk egy $r$ véletlen számot a $[0,1]$ intervallumon. Ha azt tapasztaljuk, hogy $r < W$ , akkor megfordítjuk a kiszemelt spint, különben nem változtatunk az állásán.

4.	Visszatérünk az 1. ponthoz.

Belátható, hogy a fenti algoritmussal elegendő számú ciklus után a mágnesezettség beáll valamekkora

〈 M 〉

egyensúlyi értékre, melyet a

T

hőmérséklet és a külső

H

mágneses tér határoz meg. Bizonyos számú iterációra (időre) mindig szükség van, hogy elérjük az egyensúlyi állapotot. Ez az állapot

T_{rel}

idő (az ún. relaxációs idő) után áll be. Az időt Monte-Carlo-lépésekben (MCS) szokták számolni. Egy MCS az az idő, ami alatt átlagosan minden spint egyszer kiválasztunk az iterációk során. A 4. ábrán a mágnesezettség tipikus időbeli változása (a ciklusok számától való függése) látható.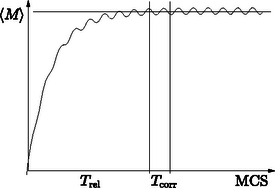

4. ábra. A mágnesezettség időbeni függése az iterációk során MCS egységekben

A relaxációs időt tapasztalat útján állapíthatjuk meg. Ha az

M

mágnesezettség már nem változik jelentősen, csak kissé ingadozik, akkor elértük az egyensúlyi állapotot. Ekkor az átlagos

〈 M 〉

mágnesezettséget úgy határozhatjuk meg, hogy bizonyos gyakorisággal kiszámoljuk

M

értékét, és vesszük ezek átlagát. A hőmérséklet változtatásával vizsgálhatjuk az átlagos mágnesezettség viselkedését, ,,méréseinkkel'' meghatározhatjuk annak hőmérsékletfüggését.
A fenti kétdimenziós végtelen Ising-modell viselkedését elsőként L. Onsager [2] számolta ki analitikusan (közelítésmentesen, zárt alakban) külső mágneses tér nélküli esetben. A rendszer kritikus hőmérséklete

k T_{c} = 2, 27 J

. Az egzakt megoldás ismeretében lehetőség van a Monte-Carlo-módszer pontosságának tanulmányozására. Jelenleg nem ismeretes analitikus megoldás három dimenzióban (vagyis térbeli rácsokra), Monte-Carlo-módszerrel azonban már alaposan tanulmányozták ezeket a rendszereket is.
A Monte-Carlo-módszer alkalmazásánál figyelni kell a lehetséges hibaforrásokra. Például a rendszer véges mérete miatt a kritikus hőmérséklet síkbeli rácsoknál nem egyezik meg az ismert elméleti értékkel. Ilyenkor vizsgálni kell, hogy hogyan függ a véges méretű mintán kapott kritikus hőmérséklet a minta méretétől, és ebből tudunk következtetni a végtelen rendszerre.
A másik gyakori gond a ,,jó'' véletlenszámgenerátor. Előfordul, hogy a generátor egymást követő számai nem teljesen függetlenek egymástól; ekkor biztosan hibás eredményeket kapunk. Rendkívül fontos tehát a véletlenszámgenerátor tesztelése.
Végezetül megemlítjük, hogy viszonylag egyszerűen programozható problémák találhatók [3] cikkben.

Köszönetemet szeretném kifejezni kollégáimnak, Kertész Jánosnak és Vicsek Tamásnak, akik megismertettek a Monte-Carlo-módszerrel, Geszti Tamásnak és Pollner Péternek a hasznos tanácsaikért, valamint egyetemi hallgatóimnak, Koltai Jánosnak, Pafka Szilárdnak és Szűcs Józsefnek, akik segítségemre voltak ebben a munkában.

Irodalom

[1]	N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 21 (1953), 1087.

[2]	L. Onsager, Phys. Rev., 65 (1944), 117.

[3]	J. Kertész, J. Cserti and J. Szép: Monte Carlo simulation programs for microcomputer, Eur. J. Phys., 6 (1985), 232.