Kezdőlap


Cím:	A munkára fogott véletlen I. rész
Szerző(k):	Cserti József
Füzet:	2003/október, 432 - 436. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A munkára fogott véletlen
I. rész

A pécsi Zipernowsky Károly szakközépiskolai tanárom,
Balog József tiszteletére
Cserti József
ELTE Komplex Rendszerek Fizikája Tanszék

A Monte-Carlo-módszer

Mindennapi életünket gyakran befolyásolják a véletlen események. Jól tudjuk, hogy a játékkaszinókban a véletlen alapvető szerepet játszik. Számos véletlen jelenséget figyelhetünk meg a környezetünkben is (például a hegyére állított ceruza dőlési iránya). A természetben is számtalan véletlen jelenséget ismerünk. Egy tartályban lévő gázatomok véletlenszerűen mozognak. Az atommagok bomlása is véletlen folyamat.
A véletlen segítségével közelítőleg meghatározhatjuk a

π

értékét. Dobjunk rizsszemeket (véletlenszerűen) egy

a

oldalú négyzetlapra, amelybe egy

a

átmérőjű kört is berajzoltunk! Végezzünk

N

számú kísérletet (csak azokat a dobásokat tekintjük, melyeknél a rizsszemek nem esnek ki a négyzetből), és számoljuk meg hány esik a körbe! Jelöljük ezek számát

N_{k}

-val! Ekkor az

N_{k} / N

arány nagy számú kísérlet (

N ≫ 1

) esetén jó közelítéssel megegyezik a kör és a négyzet területének arányával, azaz

N_{k} / N = {(a / 2)}^{2} π / a^{2} = π / 4

. Így a

π

értéket

π \approx 4 N_{k} / N

alapján számíthatjuk ki. Természetesen ez módszer nem adja meg pontosan a

π

-t. Minél több kísérletet végzünk, annál pontosabb eredményt kaphatunk, feltéve, hogy a rizsszemek valóban véletlenül esnek a négyzetre.
A fenti kísérletet nem szükséges a valóságban elvégezni. A számítógéppel egyszerű programot írhatunk. Szükségünk van egy jó véletlenszám-generátorra. Ma már számos program létezik, mely a

[0,1]

intervallumon egyenletes eloszlásban generál véletlen számokat. Generáljunk egymás után kettőt, és jelöljük ezeket

x

-szel ill.

y

-nal! E két számhoz (mint számpárhoz) egy pontot rendelhetünk a koordináta-rendszer első negyedében (rizsszem helye a dobás után). Ha a pont távolságára igaz, hogy

x^{2} + y^{2} < 1

, akkor a pont az egységsugarú körön belül van. Tegyük fel, hogy a fenti algoritmust

N

-szer elvégezve

N_{k}

számú esetben esik a pont a körön belül. Hasonlóan a rizsszemek esetéhez most is a

4 N_{k} / N

arány közelíti

π

értékét.
Az alábbi táblázatban egyre növekvő számú kísérlet során kapott (közelítő)

π

értéket és a hibát tüntettük fel (a pontos érték 9 tizedesjegyre

π = 3, 141592654

\begin{matrix} \begin{matrix} N & π & relatív hiba % -ban \\ 10 & 3,6 & 14,6 \\ 10^{2} & 3,16 & 0,6 \\ 10^{3} & 3,108 & 1,1 \\ 10^{4} & 3,127 & 0,5 \\ 10^{5} & 3,135 & 0,2 \\ 10^{6} & 3,141 & 0,02 \\ 10^{7} & 3,14155 & 0,001 \end{matrix} \end{matrix}

Látható, hogy

N

növelésével egyre pontosabb értéket kapunk

π

-re. Már néhány százezer kísérlet is elég

π

-nek két tizedesjegy pontos kiszámítására. A mai számítógépekkel akár

10^{7}

számú kísérlet is egy percen belül elvégezhető. Érdemes kipróbálni!
Teljesen véletlen jelenséget felhasználva egy jól meghatározott mennyiség értékét sikerült közelíteni. A fenti módszert tovább lehet fejleszteni, és így rendkívül bonyolult feladatok megoldásra használhatjuk a véletlent. Az eljárást a Monte-Carloban található nevezetes kaszinókra utalva, Monte-Carlo-módszernek hívják és kiterjedten alkalmazzák mind a matematikában, mind a fizikában. A Monte-Carlo elnevezést Metropolis és Ulam használták először egy 1949-es cikkükben arra utalva, hogy a módszerhez szükséges véletlen számokat akár egy játékkaszinó játékeredményeiből is vehetnénk. A gyakorlatban viszont a véletlen számokat a számítógépek maguk állítják elő. A módszert már a század elején is használta néhány statisztikus, de a Monte-Carlo-módszer csak akkor indult igazán fejlődésnek, amikor Neumann, Ulam és Fermi atommagreakciókra vonatkozó bonyolult matematikai problémák számítógéppel történő közelítő megoldására használták.
Sok esetben a feladatokat csak közelítések alkalmazásával lehet megoldani. Szerencsére legtöbbször nincs is szükségünk nagyon pontos értékekre. Ilyenkor gyakran igen hatékonynak bizonyul a Monte-Carlo-módszer. A továbbiakban néhány példát szeretnénk bemutatni a módszer alkalmazására a matematikában és a fizikában. Igyekeztünk olyan problémákat választani, melyeket a mai számítógépes lehetőségek mellett középiskolai szinten vizsgálhatunk.

Matematikai alkalmazás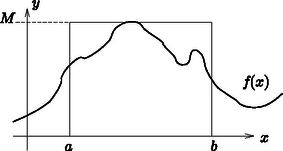

1. ábra. Egy

f (x)

függvénynek a görbe alatti területe az

[a, b]

intervallumon

Gyakori feladat egy görbe alatti terület meghatározása. Az 1. ábrán látható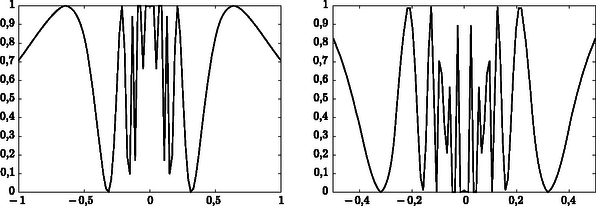

f (x)

függvénynek az

[a, b]

intervallumon a görbe alatti

A

területét úgy határozhatjuk meg, hogy az

[a, b]

szakaszt felosztjuk

N

egyenlő

Δ x = (b - a) / N

hosszúságú intervallumra, és a területet az ún. téglányösszeggel közelítjük:

\begin{matrix} A \approx \sum_{i = 1}^{N} f (x_{i}) Δ x, \end{matrix}

ahol

x_{i}

i

-edik intervallum közepe. Az egyszerűség kedvéért feltesszük, hogy a függvény pozitív az

[a, b]

szakaszon, és legyen a függvény legnagyobb értéke

M

ezen a szakaszon. A téglányösszeg annál pontosabb, minél nagyobb

N

. Ez az eljárás a legismertebb (és legegyszerűbb) módszer egy függvény görbe alatti területének meghatározására. A 2. ábrán látható

f (x) = sin^{2} (\frac{1}{x})

függvény azonban nagyon gyorsan oszcillál az origó körül, és így a terület kielégítő pontosságú kiszámításához nagyon nagyra kellene választani

N

értékét. A gyorsan változó függvények görbe alatti területét a Monte-Carlo-módszer segítségével hatékonyabban becsülhetjük meg. Ismét ,,rizsszemek'' dobálását alkalmazzuk. Generáljunk egy

x

véletlen számot (általában az egyes programnyelvekben található olyan véletlenszám-generátor, mely a

[0,1]

intervallumon egyenletes eloszlásban ad egy véletlen számot)! Ekkor az

x \to a + x (b - a)

transzformációval a kapott véletlen szám az

[a, b]

intervallumba kerül. Generáljunk egy másik

y

véletlen számot! Az

y \to y M

transzformáció után az

y

véletlen szám a

[0, M]

intervallumba esik. Tekintsük a két számot egy pont

(x, y)

koordinátáinak! Ez a pont az 1. ábrán látható

(b - a)

és

M

oldalhosszúságú téglalapon belül található. Ha viszont a pont

(x, y)

koordinátáira teljesül az

y < f (x)

egyenlőtlenség, akkor a pont (rizsszem) az

f (x)

görbe alá esik.

2. ábra. Az

f (x) = sin^{2} (1 / x)

függvény számítógéppel készített grafikonja. A függvény erősen oszcillál 0 és 1 között, ezeket az értékeket azonban a számítógépes program ,,véges felbontása'' miatt a görbe néha nem éri el. Ez pusztán egy numerikus probléma, amelyet az sem old meg, ha a görbe középső tartományát kinagyítjuk (jobb oldali ábra)

Ismételjük meg a fenti műveletsort

N_{össz}

alkalommal, és számoljuk meg hányszor esik az adott pont a görbe alá. Jelöljük ezeknek az eseményeknek a számát

N_{be}

-vel! Elegendően sok kísérlet után azt várjuk, hogy a függvény görbe alatti

A

területének és az

M (b - a)

területű téglalapnak az aránya jó közelítéssel megegyezik az

N_{be} / N_{össz}

aránnyal, és így

\begin{matrix} A \approx M (b - a) \frac{N_{be}}{N_{össz}} . \end{matrix}

Alkalmazzuk a fenti Monte-Carlo-módszert a 2. ábrán látható függvényre! Kiszámítottuk a görbe alatti területet az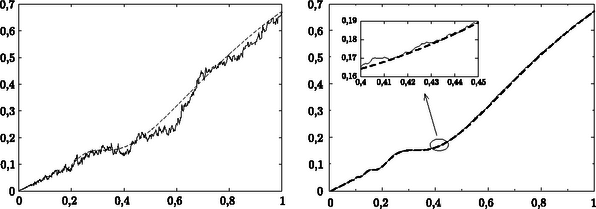

[a, b] = [0, b]

intervallumon úgy, hogy

b

értékét

0

és

1

között változtatjuk. A különböző számú kísérlet során kapott eredmények a 3. ábrán láthatók. A görbék területét általában felsőbb matematikai módszerrel, az integrálszámítással lehet kiszámítani. Ezt a módszert tekinthetjük az egzakt, azaz pontos számításnak. Az ábrákon berajzoltuk az így kapott eredményeket is a Monte-Carlo-módszer hatékonyságának illusztrálása érdekében. Látható, hogy

N_{össz} = 100

kísérlet esetén a Monte-Carlo-módszer még elég nagy hibával közelíti a pontos eredményt. Ugyanakkor

N_{össz} = 10 000

kísérlet során már nagyon jó egyezést kapunk az integrálszámításból nyert pontos eredménnyel.

3. ábra. Az

f (x) = sin^{2} (1 / x)

függvénynek a görbe alatti területe

N_{össz} = 100

(bal oldali ábra) és

N_{össz} = 10 000

(jobb oldali ábra) kísérlet során.
Az egzakt eredményt a szaggatott görbe mutatja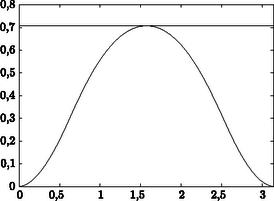

4. ábra. A ,,kalapfüggvény''. A

[0, π]

intervallumon a függvény maximuma:

M = sin^{2} (1) = 0, 7081

A továbbiakban szükségünk lesz a 4. ábrán látható

\begin{matrix} f (x) = sin^{2} (sin (x)) \end{matrix}

,,kalapszerű'' függvénynek a görbe alatti területére a

[0, π]

intervallumon. Ez a terület a Monte-Carlo-módszer alapján

A \approx 1, 2194

, melyet

\begin{matrix} N_{össz} = 2^{22} = 4 194 304 \end{matrix}

számú kísérlet elvégzése után kaptunk, három tizedesjegy pontosan egyezik az integrálszámítással kapott

A = 1, 2191

pontos eredménnyel.
A Monte-Carlo-módszert rendkívül sokféle területen használják a fizikusok is. Cikkünk II. részében a véletlenen alapuló számítási módszerek fizikai alkalmazásaiból mutatunk be néhányat.