Cím:	A 2001/2002. tanévi fizika OKTV II. fordulójának feladatmegoldásai
Füzet:	2003/április, 235 - 243. oldal	PDF  |  MathML
Témakör(ök):	OKTV

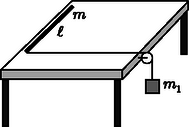
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Holics László   I. kategória   1. feladat. Vízszintes asztalra $\ell$ hosszúságú, $m$ tömegű homogén lécet fektetünk. A léc egyik végéhez a lécre merőleges helyzetű, csigán átvetett fonalat erősítünk, amelyre $m_1$ tömegű nehezéket akasztunk. A csiga tömege és a súrlódás mindenhol elhanyagolható.     1. ábra   $a)$ A léc melyik pontjának nem lesz gyorsulása a nehezék elengedésének pillanatában?     2. ábra   $b)$ Milyen tömegaránynál lesz a léc középpontjának gyorsulása maximális a nehezék elengedésének pillanatában? Mekkora ez a gyorsulás? 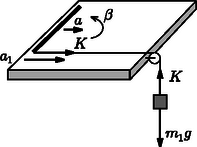() (Jurisits József)   Megoldás. $a)$ A középpont gyorsulását $a$-val, a kerületi pont gyorsulását $a_1$-gyel, a szöggyorsulást $\beta$-val jelölve a kezdeti pillanatban a következő összefüggések érvényesek: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle m_{1}g-K=m_{1}a\mathrm{,}}\hfill & \hfill {\displaystyle K=ma\mathrm{,}}\hfill \\ \hfill {\displaystyle K\cdot \frac{\ell }{2}=\frac{1}{12}m{\ell }^2\cdot \beta \mathrm{,}}\hfill & \hfill {\displaystyle \beta \cdot \frac{\ell }{2}=a_1-a\mathrm{.}}\hfill \end{array}}}\end{array}$ Az egyenletrendszer megoldásából     3. 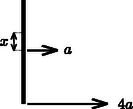ábra   $\begin{array}{c}{\displaystyle a=\frac{g}{4+\frac{m}{m_1}}\mathrm{,}{a}_1=4a\mathrm{,}\beta =\frac{6a}{\ell }\mathrm{.}}\end{array}$ A középpont túlsó oldalán lévő pontok tangenciális gyorsulása hátrafelé irányul. A középponttól $x$ távolságra lévő pontnak akkor nincs gyorsulása, ha a tangenciális gyorsulás egyenlő nagyságú a középpont gyorsulásával: $\begin{array}{c}{\displaystyle x\cdot \beta =a\mathrm{,}\text{ahonnan}x=\frac{\ell }{6}\mathrm{.}}\end{array}$ $b)$ A középpont korábban kiszámított gyorsulása $m\ll m_1$ esetén a legnagyobb, nevezetesen $\begin{array}{c}{\displaystyle a_{\underset{}{\overset{}{\text{max}}}}=\frac{g}{4}\mathrm{.}}\end{array}$     4. 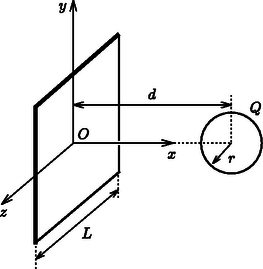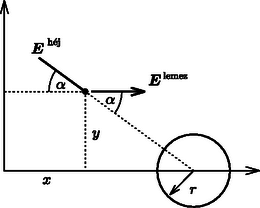ábra   2. feladat. Egy $L$ oldalú, elhanyagolható vastagságú, nagy, négyzetes szigetelő lemez $100\text{Q}$ töltéssel egyenletesen fel van töltve. Legyen a lemez síkja az $x$‐$y$ sík! Egy $r$ sugarú, $Q$ töltéssel egyenletesen töltött vékonyfalú, belül üres szigetelő gömb középpontja a síkkal szemben a $\left(d\mathrm{,0,0}\right)$ pontban helyezkedik el. Számítsuk ki az elektromos térerősséget a gömb belső pontjaiban és a $\left(d/\mathrm{2,}d/\mathrm{2,0}\right)$ pontban! Legyen $L=100d$ és $r=d/5$. Az eredményt $Q$, $d$ és az ${\epsilon }_0$ dielektromos állandó kifejezéseként adjuk meg! () (Varga Zsuzsa)   Megoldás. A lemeztől származó térerősség a Gauss-törvény alapján $\begin{array}{c}{\displaystyle E_x^{\text{lemez}}=5\cdot {10}^{-3}\frac{Q}{{\epsilon }_0{d}^2}\mathrm{,}\left(x>0\right)\mathrm{,}{E}_y^{\text{lemez}}=0.}\end{array}$ A feltöltött gömb által létrehozott elektromos mező a gömb belsejében nulla, rajta kívül pedig olyan, mintha egy $Q$ nagyságú ponttöltés lenne a gömb középpontjában (Gauss-törvény). $a)$ A gömb belső pontjaiban az eredő térerősség: $\begin{array}{c}{\displaystyle E_x=5\cdot {10}^{-3}\frac{Q}{{\epsilon }_0{d}^2}\mathrm{,}{E}_y=\mathrm{0,}{E}_z=0.}\end{array}$     5. ábra   $b)$ A gömbön kívül a kérdéses pontban az eredő térerősség: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle E_x}& \hfill {\displaystyle =}\hfill & {\displaystyle E_x^{\text{lemez}}-E_x^{\text{héj}}\cdot \text{cos}{45}^{\circ }=-0\mathrm{,}107\frac{Q}{{\epsilon }_0{d}^2}\mathrm{,}}\hfill \\ \hfill {\displaystyle E_y}& \hfill {\displaystyle =}\hfill & {\displaystyle E_y^{\text{héj}}\cdot \text{sin}{45}^{\circ }=-0\mathrm{,}113\frac{Q}{{\epsilon }_0{d}^2}\mathrm{.}}\hfill \end{array}}}\end{array}$ Ez a vektor $\begin{array}{c}{\displaystyle E=\sqrt[]{E_x^2+E_y^2}=0\mathrm{,}156\frac{Q}{{\epsilon }_0{d}^2}}\end{array}$ nagyságú, és a negatív $x$ tengellyel $46\mathrm{,}{6}^{\circ }$-os szöget zár be.   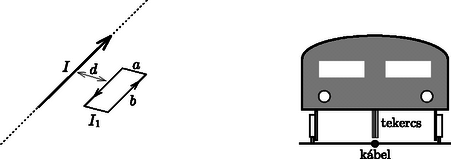3. feladat. Egy merev, téglalap alakú vezető hurok síkjában a hosszabbik oldallal párhuzamosan nagyon hosszú, $10\text{A}$ erősségű áramot szállító egyenes vezeték helyezkedik el. A téglalap oldalai $a=0\mathrm{,}2\text{m}$, $b=0\mathrm{,}3\text{m}$, a benne folyó áram erőssége $1\text{A}$. Az egyenes vezeték a huroktól $0\mathrm{,}25\text{m}$ távolságra van. Határozzuk meg a keretre ható eredő erő irányát és nagyságát!     6. ábra   Ez az elrendezés használatos az ún. mágneses lebegtetésű vonat megvalósításánál. Sok-sok függőleges síkú hurok (egy négyszögletes tekercs) van elhelyezve minden kocsiban pontosan a vágány közepén futó kábel felett. A kocsi és a tekercs azonos $b$ hosszúságú. A kocsi egységnyi hosszra eső tömege $m$ kg/m. Ha $d=1\text{cm}$, $m=100\text{kg/m}$ és a vágánybeli kábel és a tekercs árama egyaránt $100\text{A}$, hány menetesnek kell lennie a tekercsnek, ha $a\gg d$? () (Varga Zsuzsa)   Megoldás. A mágneses indukció nagysága az egyenes vezetőtől $x$ távolságban (a rajz síkjába befelé) $\begin{array}{c}{\displaystyle B\left(x\right)=\frac{{\mu }_0}{2\pi }\frac{I}{x}\mathrm{.}}\end{array}$ A téglalap alakú vezető hurok egyes darabkáira ható erő az $\text{F}=I_1\text{l}\times \text{B}$ képlet alapján számítható. A $BA$ és a $DC$ szakaszokon ható erők kiejtik egymást, így $\begin{array}{c}{\displaystyle F^{\text{eredő}}=F_{AD}-F_{CB}=\frac{{\mu }_0}{2\pi }I{I}_{1}b\left(\frac{1}{d}-\frac{1}{d+a}\right)=1\mathrm{,}067\cdot {10}^{-6}\text{N. }}\end{array}$ Az $N$ menetes tekercset tartalmazó vonat lebeg a sínen, ha (kihasználva, hogy $a\gg d$) $\begin{array}{c}{\displaystyle mgb=N{F}^{\text{eredő}}\approx \frac{N{\mu }_{0}I{I}_{1}b}{2\pi d}\mathrm{.}}\end{array}$ Ebből a megadott számadatokkal $N\approx 500$ menet adódik.   II. 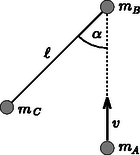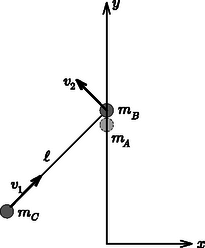kategória   1. feladat. Három azonos tömegű és méretű ($m_A=m_B=m_C=m$) lapos korong nyugszik vízszintes sima lapon. A $B$ és $C$ korong vékony, $\ell =1\text{m}$ hosszú fonállal van összekötve. A fonál kezdetben laza, de egyenes, iránya ${45}^{\circ }$-os szöget zár be az $A$ és $B$ korongok közepét összekötő egyenessel. Az $A$ korongot $v=2\text{m/s}$ sebességgel meglökjük úgy, hogy a $B$ koronggal centrálisan ütközzön. Az ütközések abszolút rugalmasak és pillanatszerűek.     7. ábra   Az $A$ és $B$ korongok ütközésétől számítva mennyi idő múlva lesz a $B$ és $C$ korongok középpontját összekötő egyenes párhuzamos az $A$ korong pályájával? Milyen távol lesz ekkor az $A$ korongtól a $B$ és $C$ korong? (Tekintsük a korongokat pontszerűeknek!) () (Holics László)     8. 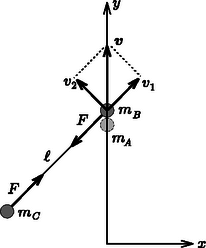ábra   Megoldás. A folyamatban két rugalmas ütközés megy végbe. Az első ütközés során (tömegük egyenlősége miatt) az $A$ és $B$ korongok ,,sebességet cserélnek'', az $A$ korong megáll, $B$ pedig $v$ sebességgel megindul.     9. ábra   Vizsgáljuk a $B$ és $C$ korongból álló rendszer további mozgását! A második rugalmas ütközés akkor következik be, amikor a fonál hirtelen megfeszül, és megrántja a végeihez kötött két korongot; egyenlő $F$ nagyságú, de ellentétes irányú erőlökést adva nekik. Ez az erőlökés a fonálra merőleges sebességkomponenseket nem tudja megváltoztatni (tehát a 8. ábrán látható jelölésekkel azok nagysága $v_2=v/\sqrt[]{2}$ és nulla marad), a fonállal párhuzamos sebességkomponensek pedig (mivel a korongok tömege megegyezik) kicserélődnek (9. ábra). A második ütközés után tehát mindkét test sebességének nagysága ugyanakkora: $\begin{array}{c}{\displaystyle u_B=u_C=v\frac{\sqrt[]{2}}{2}\mathrm{,}}\end{array}$ de a sebességük iránya egymásra merőleges. Válasszunk egy olyan koordináta-rendszert, amelynek $y$ tengelye a $\text{v}$-vel (az $A$ korong pályájával) párhuzamos, ebben a második ütközésben részt vevő testek sebessége az ütközés után: $\begin{array}{c}{\displaystyle u_{By}=-u_{Bx}=v/\mathrm{2,}}\end{array}$ illetve $\begin{array}{c}{\displaystyle u_{Cy}=u_{Cx}=v/\mathrm{2,}}\end{array}$ tehát mindkét test az $y$ tengellyel ${45}^{\circ }$-os szöget bezáró irányban mozog. A második ütközés (a fonál által kifejtett erőlökés) után a fonál azonnal meglazul, és mindkét korong erőmentesen, egyenes vonalú egyenletes mozgást végez. A két korongot összekötő egyenes akkor lesz párhuzamos az $y$ tengellyel (az $A$ korong korábbi sebességével), amikor $B$ is és $C$ is megteszi $v/2$ sebességgel az $\ell \sqrt[]{2}/4$ nagyságú ,,$x$ irányú'' távolságot. Ez a pillanat az $A$-val való ütközés után $\begin{array}{c}{\displaystyle t=\frac{\ell }{v}\cdot \frac{\sqrt[]{2}}{2}=0\mathrm{,}35\text{s }}\end{array}$ múlva következik be. Ekkor mind az $A$, mind pedig a $B$ korong $\ell /2=0\mathrm{,}5\text{m}$ távolságban lesz az $A$ korongtól, egymástól mért távolságuk pedig $\ell \sqrt[]{2}/2=0\mathrm{,}71\text{m}$.   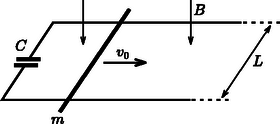2. feladat. Két párhuzamos, egymástól $L$ távolságra futó vízszintes fémsín egyik végét $C$ kapacitású, kezdetben töltetlen kondenzátorral zárjuk le. A sínpár időben állandó, függőleges irányú, $B$ indukciójú homogén mágneses mezőben van. A sínpárra merőlegesen egy $R$ ellenállású, $m$ tömegű vezető rudat fektetünk, amit $v_0$ sebességgel meglökünk. Mekkora sebességre lassul le a rúd, ha a sín elegendően hosszú, és a mágneses tér is kellően kiterjedt? (A sín elektromos ellenállása, a súrlódás és az önindukciós hatások elhanyagolhatók.) () (Szegedi Ervin)     10. ábra   Megoldás. A rúd indítását követően a mozgási indukció jelensége miatt feszültség indukálódik, indukált áram folyik, és a kondenzátor elkezd feltöltődni. A pillanatnyi áramerősséget az indukált feszültség és a kondenzátor feszültsége határozza meg: $\begin{array}{c}{\displaystyle Ri\left(t\right)=BLv\left(t\right)-\frac{Q\left(t\right)}{C}\mathrm{.}}\end{array}$ A mágneses térben mozgó, áramjárta rúdra fékező mágneses erő hat, ezért a rúd sebessége csökken. Ez a sebességcsökkenés mindaddig tart, amíg áram folyik, azaz amíg az indukált feszültség és a kondenzátor feszültsége ,,ki nem oltja'' egymást: $\begin{array}{c}{\displaystyle BL{v}_{\underset{}{\overset{}{\text{min}}}}=\frac{Q_{\underset{}{\overset{}{\text{max}}}}}{C}\mathrm{.}}\end{array}$ (1) A dinamika alaptörvénye alapján $\begin{array}{c}{\displaystyle m\frac{\Delta v}{\Delta t}=-BiL\mathrm{,}}\end{array}$ ahonnan $i\Delta t=\Delta Q$ felhasználásával $\begin{array}{c}{\displaystyle m\Delta v=-BL\Delta Q\mathrm{.}}\end{array}$ Ha az indulástól a sebesség állandósulásáig elemi részekre osztjuk a mozgást, és a fenti összefüggést minden részre felírjuk, majd azokat összegezzük $\begin{array}{c}{\displaystyle m\left(v_{\underset{}{\overset{}{\text{min}}}}-v_0\right)=-BL\Delta Q_{\underset{}{\overset{}{\text{max}}}}}\end{array}$ adódik. 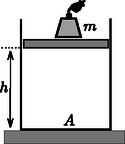Ebből (1) felhasználásával $\begin{array}{c}{\displaystyle v_{\underset{}{\overset{}{\text{min}}}}=\frac{m}{m+{\left(BL\right)}^{2}C}{v}_0\mathrm{.}}\end{array}$   3. feladat. Egy $A=1\text{d<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}$ alapterületű, függőlegesen álló hengerben lévő levegőt elhanyagolható tömegű, súrlódásmentesen mozgó dugattyú zár el a külső levegőtől. A levegőoszlop magassága $h=5\text{dm}$. A dugattyúra óvatosan egy $m=14\text{kg}$ tömegű nehezéket helyezünk, majd elengedjük azt. A dugattyú és a nehezék kis amplitúdójú, jó közelítéssel harmonikus rezgőmozgásba kezd. Határozzuk meg a rezgés amplitúdóját, frekvenciáját és a dugattyú maximális sebességét!     11. ábra   (A henger fala hőszigetelőnek tekinthető. A külső légnyomás $p_{\text{k}}=100\text{kPa}$. Szükség esetén használjuk a következő közelítést: ${\left(1\pm x\right)}^n\approx 1\pm nx$, ha $x$ nullához közeli érték.) () (Szegedi Ervin)   Megoldás. Ha a dugattyú‐teher rendszer a kiindulási helyzetből $x$ távolsággal elmozdul lefelé, akkor a rá ható eredő erő $\begin{array}{c}{\displaystyle F\left(x\right)=mg-\left(p-p_{\text{k}}\right)A\mathrm{,}}\end{array}$ (1) ahol $p$ a levegő megnövekedett nyomása. Mivel az állapotváltozás adiabatikus, és a bezárt gáz térfogata a levegőoszlop magasságával arányos: $\begin{array}{c}{\displaystyle p_{\text{k}}\cdot h^{\kappa }=p\cdot {\left(h-x\right)}^{\kappa }\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle p=p_{\text{k}}{\left(\frac{h}{h-x}\right)}^{\kappa }\approx p_{\text{k}}\left(1+\kappa \frac{x}{h}\right)\mathrm{.}}\end{array}$ (2) (1) és (2) összevetésével a dugattyú‐teher rendszerre ható eredő erő Ezt a kifejezést $F\left(x\right)=-D\left(x-x_0\right)$ alakban is írhatjuk, ahol Ez az erőtörvény ‐ a függőleges rugóra akasztott test példájához hasonlóan ‐ $x_0$ egyensúlyi helyzet körüli harmonikus rezgőmozgást ír le. Mivel a test a rezgés szélső helyzetéből indult, a rezgés amplitúdója is $x_0$, tehát 5 cm. A rezgés frekvenciája $\begin{array}{c}{\displaystyle f=\frac{1}{2\pi }\sqrt[]{\frac{D}{m}}=2\mathrm{,}25\text{Hz, }}\end{array}$ a dugattyú maximális sebessége pedig $\begin{array}{c}{\displaystyle v_{\underset{}{\overset{}{\text{max}}}}=x_{0}2\pi f=0\mathrm{,}71\frac{\text{m}}{\text{s}}\mathrm{.}}\end{array}$   III. kategória   Az 1. és 3. feladat megegyezik a II. kategória megfelelő feladatával.   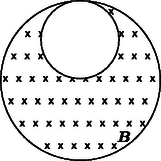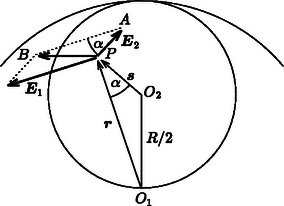2. feladat. Egy $R=10\text{cm}$ sugarú, hosszú henger belsejében egy vele párhuzamos tengelyű, $R/2$ sugarú kisebb henger helyezkedik el, ami belülről érinti a nagyobb hengert. A kisebb hengerben nincs mágneses mező, a nagyobb henger maradék részében időben egyenletesen változó, homogén eloszlású mágneses mező van. Az indukció változási gyorsasága $\Delta B/\Delta t=80\text{V/<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>.}$ A mágneses indukció párhuzamos a henger tengelyével.     12. ábra   Határozzuk meg az indukált elektromos mező térerősségét a kisebb henger belsejében! () (Szegedi Ervin)   Megoldás. Ha a nagyobb hengert teljesen kitöltené a változó mágneses mező, akkor a belsejében a tengelyétől $r$ távolságban $\left(r\le R\right)$ az indukált elektromos mező a szimmetria miatt ,,érintőleges'', és nagyságát az indukciótörvény határozza meg: $\begin{array}{c}{\displaystyle 2r\pi \cdot E=\frac{\Delta B}{\Delta t}\cdot r^2\pi \mathrm{,}\text{azaz}E=\frac{r}{2}\cdot \frac{\Delta B}{\Delta t}\mathrm{.}}\end{array}$ Képzeljük el, hogy a feladatban szereplő mágneses mező úgy jön létre, hogy két, időben változó mágneses mező szuperponálódik: (i) egy egyenletesen változó, homogén $\text{<span style="font-weight: bold;"><span style="font-style: italic;">B</span></span>}\left(t\right)$ tér, ami a nagy hengert teljesen kitölti, és (ii) egy $-\text{<span style="font-weight: bold;"><span style="font-style: italic;">B</span></span>}\left(t\right)$-vel jellemezhető mező, ami csak a kis henger belsejében van.     13. ábra   A kis henger valamely $P$ belső pontja legyen a nagy henger $O_1$ középpontjától $r$ távolságra, a kis henger $O_2$ középpontjától $s$ távolságra, és a megfelelő vektorokat jelöljük $\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}$-rel, illetve $\text{<span style="font-weight: bold;"><span style="font-style: italic;">s</span></span>}$-sel (lásd a 13. ábrát). Ekkor $P$-ben az indukált $\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}$ elektromos mező két indukált térerősségből szuperponálható: $\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}={\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_1+{\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_2$, ahol Mivel ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_1\perp \text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}$ és ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_2\perp \text{<span style="font-weight: bold;"><span style="font-style: italic;">s</span></span>}$, az $O_{2}P{O}_1$ és a $PAB$ háromszögeknek van egy közös szöge $\left(\alpha \right)$. Másrészt $\begin{array}{c}{\displaystyle \frac{AB}{AP}=\frac{E_1}{E_2}=\frac{r}{s}=\frac{O_{1}P}{O_{2}P}}\end{array}$ miatt a két háromszögben az egyenlő szöget közrefogó oldalak aránya is egyenlő, tehát a két háromszög hasonló. Ezért $\begin{array}{c}{\displaystyle \frac{BP}{AB}=\frac{E}{E_1}=\frac{O_1{O}_2}{O_{1}P}=\frac{R}{2r}\mathrm{,}\text{vagyis}E=E_1\cdot \frac{R}{2r}=\frac{R}{4}\frac{\Delta B}{\Delta t}=2\mathrm{,}0\frac{\text{V}}{\text{m}}\mathrm{.}}\end{array}$ Másrészt $\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}$ merőleges az $O_1{O}_2$ egyenesre, vagyis $\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}$-nek nemcsak a nagysága, de az iránya is független a $P$ pont helyzetétől, tehát a kisebb hengerben az indukált elektromos mező homogén.   A verseny végeredménye I. kategória   1.  Sipos Barnabás (Budapest, Trefort Ágoston Kéttannyelvű Szki., 12. évf.), tanára: Fülöp László; 2.  Szarvas Tamás (Budapest, Puskás Tivadar Távközlési Techn., 12. évf.), tanára: Beregszászi Zoltán; 3.  Mendli Bálint (Budapest, Puskás Tivadar Távközlési Techn., 12. évf.), tanára: Beregszászi Zoltán; 4. Juhász Gábor (Vác, Boronkay György Műszaki Szki., 12. évf.); 5. Drahos Tamás (Miskolc, Bláthy Ottó Villamosipari Szki., 11. évf.); 6. Pszota Zsolt (Vác, Boronkay György Műszaki Szki., 12. évf.); 7. Cserháti Sándor (Győr, Pattantyús Géza Ipari Szki., 12. évf.); 8. Simon Tamás (Budapest, Puskás Tivadar Távközlési Techn., 11. évf.); 9. Varga Gábor (Budapest, Alternatív Közgazdasági Gimn., 12. évf.); 10. Koltay Szabolcs (Budapest, Puskás Tivadar Távközlési Techn., 12. évf.).   II. kategória   1.  Siroki László (Debrecen, Fazekas Mihály Gimn., 12. évf.), tanára: Simon Gyula; 2.  Nagy Márton (Budapest, Piarista Gimn., 12. évf.), tanárai: Futó Béla; 3.  Vehovszky Balázs (Budapest, Piarista Gimn., 11. évf.), tanára: Futó Béla; 4. Balogh László (Fazekas Mihály Főv. Gyak. Gimn., 11. évf.); 5. Nagy Zoltán Lóránt (Fazekas Mihály Főv. Gyak. Gimn., 11. évf.); 6. Pápai Tivadar (Barcs, Dráva Völgye Középisk., 12. évf.); 7. Tóth Sándor (Csongrád, Batsányi János. Gimn., 11. évf.); 8. Dolgos Gergely (Budapest, Árpád Gimn., 12. évf.),; 9. Rácz Éva (Fazekas Mihály Főv. Gyak. Gimn., 11. évf.); 10. Kiss Demeter (Fazekas Mihály Főv. Gyak. Gimn., 11. évf.).   III. kategória   1.  Pallos Péter (Fazekas Mihály Főv. Gyak. Gimn., 12. évf.), tanára: Horváth Gábor; 2.  Nagy Szabolcs (ELTE Trefort Ágoston Gyak. Gimn., 12. évf.), tanára: Chikán Éva; 3.  Béky Bence (Fazekas Mihály Főv. Gyak. Gimn., 12. évf.), tanára: Horváth Gábor; 4. Sparing Dániel (ELTE Radnóti Miklós Gyak. Gimn., 11. évf.); 5. Szekeres Balázs (Szolnok, Verseghy Ferenc Gimn., 11. évf.); 6. Szilva Attila (Miskolc, Földes Ferenc Gimn., 12. évf.); 7. Antal Ágnes (ELTE Apáczai Csere János Gyak. Gimn., 12. évf.); 8. Fejős Gergely (ELTE Radnóti Miklós Gyak. Gimn., 11. évf.); 9. Harangi Viktor (Fazekas Mihály Főv. Gyak. Gimn., 12. évf.); 10. Szalai Bence (Lovassy László Gimn., 12. évf.).