|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Bevezető
2005 májusában új kétszintű vizsga várja az érettségizőket. Ebben a mellékletben elsősorban ennek a vizsgának a matematika fejezetével kapcsolatos információkat szeretnénk nyilvánosságra hozni. A vizsga leírása mellett a 2003 tavaszán ,,beüzemelt'' próbafeladatsorokat, illetve ezek javítási útmutatóit közöljük, remélve, hogy diák és tanár felkészülését egyaránt segítik. Felhívjuk a figyelmet egyrészt arra, hogy a jelenlegi feladatsorok 11. osztályosoknak készültek, ezért a majdani feladatsorokban lehetnek más típusú feladatok is; másrészt arra, hogy ezek a próbaérettségik nem az érettségi színvonalának bemutatására, hanem az érettségiztetés szervezésének, ütemezésének előkészítésére születtek.
Emellett a ,,hagyományos'' vizsgákra készülőkre is gondoltunk. Rábai Imre Tanár Úrnak a 2003 májusi számunkban közölt felvételi előkészítő feladatainak megoldásait, illetve a nemrég elhunyt Scharnitzky Viktor 20 feladatát és megoldásukat tanulmányozva olvasóink maguk vethetik egybe a középiskolát záró matematikavizsgák eddigi és eljövendő követelményeit.
Köszönjük a Kiss Árpád Országos Közoktatási Szolgáltató Intézmény vezetőjének és munkatársainak, és Scharnitzky Viktor özvegyének segítő közreműködését.
A MATEMATIKA ÉRETTSÉGI VIZSGA
ÁLTALÁNOS KÖVETELMÉNYEI A vizsga formája
Középszinten: írásbeli
Emelt szinten: írásbeli és szóbeli
A matematika érettségi vizsga célja
A matematika érettségi vizsga célja annak vizsgálata, hogy a vizsgázó
| | tud-e logikusan gondolkodni, rendelkezik-e megfelelő matematikai probléma- és feladatmegoldó, valamint absztrakciós, analizáló és szintetizáló képességgel; |
| | tud-e állításokat, egyszerűbb gondolatmenetű bizonyításokat szabatosan megfogalmazni, áttekinthető formában leírni; |
| | elsajátította-e a mindennapi életben használatos számolási technikákat, rendelkezik-e biztos becslési készséggel, az önellenőrzés igényével; |
| | képes-e statisztikai gondolatok megértésére, intelligens felhasználására, a függvény- vagy függvényszerű kapcsolatok felismerésére és értékelésére; |
| | képes-e a leírt síkbeli és térbeli szituációk elképzelésére, tud-e ezekhez ábrát készíteni, s ennek segítségével az adott konstrukcióban gondolkodni, számolni; |
| | képes-e a tanult ismereteket más tantárgyakhoz kapcsolódó feladatokban alkotó módon alkalmazni; |
| | képes-e hétköznapi szövegben rejlő matematikai problémákat észrevenni, egy-egy gyakorlati kérdés megoldásához matematikai modellt alkotni, különböző problémamegoldó stratégiákat alkalmazni; |
| | képes-e a különböző matematikai segédeszközök (függvénytáblázat, zsebszámológép) célszerű alkalmazására; a mindenkori tárgyi feltételek függvényében, azokkal szinkronban a matematikai eszközökkel való problémamegoldásban a programozható számológép, a grafikus kalkulátor és a számítógép használata fokozatosan követelménnyé válhat. |
Az emelt szinten a felsoroltakon túl az érettségi vizsga célja annak mérése, hogy a tanuló
| | rendelkezik-e a felsőfokú matematikai tanulmányokhoz szükséges alapokkal; |
| | képes-e hipotéziseket megfogalmazni, és sejtéseit bizonyított állításaitól megkülönböztetni; |
| | milyen szintű kombinatív készséggel rendelkezik, mennyire kreatív a gondolkodása; |
| | képes-e gondolatmenetében érthetően, világosan alkalmazni a matematikai modellalkotás lépéseit (probléma megfogalmazása, matematikai formába öntése, összefüggések keresése, az eredmények matematikai módszerekkel történő kiszámítása, igazolása, értelmezése); |
Az ismeretek legnagyobb része a középszinten és az emelt szinten egyaránt megjelenik. Ezen ismeretek feldolgozásában az emelt szintet az igényesebb felépítés, az összetettebb alkalmazás, a nehezebb feladatok jellemzik. A követelmények leírásában gyakran szereplő ,,szemléletes'' jelző azt fejezi ki, hogy az adott fogalom matematikailag precíz ismerete nem követelmény. A matematika tanításában csak spirálisan lehet haladni, s így több téma, pl. az analízis ‐ a felkészülésre fordítható idő alatt ‐ a középiskolai tanulmányok végére is csak szemléletes formában tanítható meg, s csak bizonyos alkalmazásokat tesz lehetővé.
I. RÉSZLETES ÉRETTSÉGI VIZSGAKÖVETELMÉNY
Az érettségi követelményeit két szinten határozzuk meg:
középszinten a mai társadalomban tájékozódni és alkotni tudó ember matematikai ismereteit kell megkövetelni, ami elsősorban a matematikai fogalmak, tételek gyakorlati helyzetekben való ismeretét és alkalmazását jelenti;
az emelt szint tartalmazza a középszint követelményeit, de az azonos módon megfogalmazott követelmények körében az emelt szinten nehezebb, több ötletet igénylő feladatok szerepelnek. Ezen túlmenően az emelt szint követelményei között speciális anyagrészek is találhatók, mivel emelt szinten elsősorban a felsőoktatásban matematikát használó, illetve tanuló diákok felkészítése történik.
KOMPETENCIÁK
Gondolkodási módszerek, halmazok, logika, kombinatorika, gráfok
| | Legyen képes a tanuló adott szövegben rejlő matematikai problémákat észrevenni, szükség esetén matematikai modellt alkotni, a modell alapján számításokat végezni, és a kapott eredményeket értelmezni. |
| | Legyen képes kijelentéseket szabatosan megfogalmazni, azokat összekapcsolni, kijelentések igazságtartalmát megállapítani. |
| | Lássa az eltéréseket, illetve a kapcsolatokat a matematikai és a mindennapi nyelv között. |
| | A matematika minden területén és más tantárgyakban is tudja alkalmazni a halmaz fogalmát, illetve a halmazműveleteket. |
| | Legyen jártas alapvető kombinatorikus gondolatmenetek alkalmazásában, s legyen képes ennek segítségével gyakorlati sorbarendezési és kiválasztási feladatok megoldására. |
| | Ismerje a gráfok jelentőségét, sokoldalú felhasználhatóságuk néhány területét, és legyen képes további felhasználási lehetőségek felismerésére a gyakorlati életben és más tudományágakban. |
| | Az emelt szinten érettségiző diák ismerje a halmazelmélet alapvető szerepét a mai matematika felépítésében. |
Számelmélet, algebra
| | Legyen képes a tanuló betűs kifejezések értelmezésére, ismerje fel használatuk szükségességét, tudja azokat kezelni, lássa, hogy mi van a ,,betűk mögött''. |
| | Ismerje az egyenlet és az egyenlőtlenség fogalmát, megoldási módszereit (pl. algebrai, grafikus, közelítő). |
| | Legyen képes egy adott probléma megoldására felírni egyenleteket, egyenletrendszereket, egyenlőtlenségeket, egyenlőtlenség-rendszereket. |
| | Tudja az eredményeket előre megbecsülni, állapítsa meg, hogy a kapott eredmény reális-e. |
| | Az emelt szinten érettségiző diáknak legyen jártassága az összetettebb algebrai átalakításokat igénylő feladatok megoldásában is. |
Függvények, az analízis elemei
| | Legyen képes a tanuló a körülötte levő világ egyszerűbb összefüggéseinek függvényszerű megjelenítésére, ezek elemzéséből tudjon következtetni valóságos jelenségek várható lefolyására. |
| | Legyen képes a változó mennyiségek közötti kapcsolat felismerésére, a függés értelmezésére. Értse, hogy a függvény matematikai fogalom, két halmaz elemeinek egymáshoz rendelése. Ismerje fel a hozzárendelés formáját, elemezze a halmazok közötti kapcsolatokat. |
| | Lássa, hogy a sorozat diszkrét folyamatok megjelenítésére alkalmas matematikai eszköz, a pozitív egész számok halmazán értelmezett függvény. Ismerje a számtani és mértani sorozatot. |
| | Az emelt szinten érettségiző diák ismerje az analízis néhány alapelemét, amelyekre más szaktudományokban is (pl. fizika) szüksége lehet. Ezek segítségével tudjon függvényvizsgálatokat végezni, szélsőértéket, görbe alatti területet számolni. |
Geometria, koordinátageometria, trigonometria
| | Tudjon a tanuló síkban, illetve térben tájékozódni, térbeli viszonyokat elképzelni, tudja a háromdimenziós valóságot ‐ alkalmas síkmetszetekkel ‐ két dimenzióban vizsgálni. |
| | Vegye észre a szimmetriákat, tudja ezek egyszerűsítő hatásait problémák megfogalmazásában, bizonyításokban, számításokban kihasználni. |
| | Tudjon a feladatok megoldásához megfelelő ábrát készíteni. |
| | Tudjon mérni és számolni hosszúságot, területet, felszínt, térfogatot, legyen tisztában a mérési pontosság fogalmával. |
| | Ismerje a geometria szerepét a műszaki életben és bizonyos képzőművészeti alkotásokban. |
| | Az emelt szinten érettségiző diák tudja szabatosan megfogalmazni a geometriai bizonyítások gondolatmenetét. |
Valószínűségszámítás, statisztika
| | Értse a tanuló a statisztikai kijelentések és gondolatmenetek sajátos természetét. |
| | Ismerje a statisztikai állítások igazolására felhasználható adatok gyűjtésének lehetséges formáit, és legyen jártas a kapott adatok áttekinthető szemléltetésében, különböző statisztikai mutatókkal való jellemzésében. |
| | Az emelt szinten érettségiző diák tudjon egyszerűbb véletlenszerű jelenségeket modellezni és a valószínűségi modellben számításokat végezni. |
| | Emelt szinten ismerje a véletlen szerepét egyszerű statisztikai mintavételi eljárásokban. |
II. A VIZSGA LEÍRÁSA
KÖZÉPSZINTŰ VIZSGA
A vizsga szerkezete
A középszintű matematika érettségi 180 perces írásbeli vizsga. Szóbeli vizsgát azok a tanulók tehetnek, akiknek az írásbeli vizsgájuk sikertelen (nem érték el az elégséges szintet), de az írásbeli vizsgapontszám 10%-át elérték. Mind az írásbeli, mind pedig a szóbeli vizsgán használható függvénytáblázat és számológép. Ezek paramétereit az egyes években kell meghatározni.
Írásbeli vizsga
Tartalmi szerkezet
A feladatsor tematikailag lefedi a követelményrendszer 5 nagy témakörét.
A feladatsor összeállításakor az alábbi tartalmi arányok az irányadók:
Ezek az arányok természetesen csak hozzávetőlegesek lehetnek, hiszen a feladatok egy jelentős része több témakörbe is besorolható, összetett ismeretkörre épül, továbbá a feladatsor választható feladatokat tartalmazó részei miatt az egyes tanulók számára ‐ a választásaiktól függően ‐ az arányok eltolódhatnak. Az első témakörbe tartozik a feladatoknak minden olyan részeleme, amely a szöveg matematikai nyelvre való lefordítását, matematikai modellalkotást igényel.
A feladatsor feladatainak 30‐50%-a a hétköznapi élet problémáiból indul ki, esetenként egyszerű modellalkotást igénylő feladat.
A feladatsor jellemzői
A feladatsor két, jól elkülönülő részből áll.
Az I. rész 10-12 feladatot tartalmazó feladatlap, amely az alapfogalmak, definíciók, egyszerű összefüggések ismeretét hivatott ellenőrizni. Ebben a részben megjelenhet néhány igaz-hamis állítást tartalmazó vagy egyszerű feleletválasztós feladat is, de a feladatok többsége nyílt végű. Az első rész megoldására 45 perc áll rendelkezésre, vagyis ezen idő eltelte után e feladatok megoldására nincs tovább mód.
A feladatsor I. részében összesen 30 pont érhető el.
A II. rész megoldási időtartama 135 perc. Ez további két részre oszlik, melynek megoldása folyamatos, az adott időn belül nem korlátozott.
A II./a rész 4, egyenként 12 pontos feladatot tartalmaz, amelyből 3-at kell megoldani, és csak ez a három értékelhető. Tehát a jelöltnek a négyből egyértelműen ki kell választania az értékelendő három feladatot. A feladatok egy vagy több kérdésből állnak.
A II./b rész 3, egyenként 17 pontos feladatot tartalmaz, amelyből 2-t kell megoldani, és csak ez a kettő értékelhető, a II./a részben leírtakhoz hasonlóan. A feladatok a középszintű követelmények keretein belül összetett feladatok, általában több témakört is érintenek és több részkérdésből állnak.
A II./a és II./b rész megoldására fordított időt a jelölt szabadon használhatja fel.
A vizsga bevezetését követő első években választás csak a II./b részben lesz felajánlva, tehát a II./a részben 3 kötelezően megoldandó feladatot tűzünk ki.
Értékelés
Az írásbeli vizsgán elérhető pontszám 100 pont.
A dolgozatok javítására részletes javítási útmutató szolgál. A javítási útmutató tartalmazza a feladatok részletes megoldását, esetenként több változatot is, valamint az egyes megoldási lépésekre adható részpontszámokat.
Szóbeli vizsga
Tartalmi szerkezet
A szóbeli vizsgára legalább 20 tételt kell készíteni, amennyiben a vizsgázó csoportban van szóbeli vizsgára utasított tanuló. A tételsor tartalmi arányai az írásbeli vizsga leírásánál meghatározott arányokat tükrözzék.
A tételek jellemzői
A tétel tartalmazzon 3 egyszerű elméleti kérdést (definíciót, tételkimondást), valamint 3 feladatot. A tétel egyes elemei más-más témakörből kerüljenek kiválasztásra.
Értékelés
A szóbeli vizsgán elérhető pontszám 50 pont.
Az értékelés szempontjai:
Azt, hogy az utolsó 5 pontból mennyit kap a vizsgázó, annak a mérlegelésével kell eldönteni, hogy a jelölt milyen mértékben tudott önállóan megbirkózni a kérdésekkel, illetve a feladatokkal, ha segítő kérdésekre volt szüksége, azokat megértette-e és a feleletében fel tudta-e használni. Itt kell értékelni azt is, hogy mennyire volt logikus a felelet felépítése.
A szóbeli vizsgát is tett tanuló végső értékelése az írásbeli és a szóbeli vizsga együttes pontszáma alapján történik.
EMELT SZINTŰ VIZSGA
A vizsga szerkezete
Az emelt szintű matematika érettségi vizsga 240 perces írásbeli vizsgából és legfeljebb 20 perces szóbeli vizsgából áll. Mind az írásbeli, mind pedig a szóbeli vizsgán használható függvénytáblázat és számológép. Ezek paramétereit az egyes években kell meghatározni.
Írásbeli vizsga
Tartalmi szerkezet
A feladatsor tematikailag lefedi a követelményrendszer 5 nagy témakörét.
A feladatsor összeállításakor az alábbi arányok az irányadók:
Ezek az arányok természetesen csak hozzávetőlegesek lehetnek, hiszen a feladatok egy jelentős része több témakörbe is besorolható, összetett ismeretkörre épül, továbbá a feladatsor választható feladatokat tartalmazó részei miatt az egyes tanulók számára ‐ a választásaiktól függően ‐ az arányok eltolódhatnak. Az első témakörbe tartozik a feladatoknak minden olyan részeleme, amely a szöveg matematikai nyelvre való lefordítását, matematikai modellalkotást igényel.
A feladatsor feladatainak 30‐40%-a szöveges, a hétköznapi élet problémáiból kiinduló, egyszerű modellalkotás alkalmazását igénylő feladat.
A feladatsor jellemzői
A feladatsor folyamatosan megoldandó, 2 különböző részből áll. A jelölteknek összesen 240 perc áll a rendelkezésükre, amit szabadon használhatnak fel. Az írásbeli vizsgán elérhető összpontszám 115 pont.
Az I. rész 4 feladatból áll. Ezek az emelt szintű követelmények alapján egyszerűnek tekinthetők, többnyire a középszintű követelmények ismeretében is megoldhatók. (Ebben a részben nincs választási lehetőség.) A feladatok több részkérdést is tartalmazhatnak, az elérhető összpontszám 51.
A II. rész 5, egyenként 16 pontértékű feladatból áll. Ezek közül legalább kettőben a gyakorlati életben előforduló szituációból származik a probléma, így a megoldáshoz a vizsgázónak a szöveget le kell fordítania a matematika nyelvére, azaz matematikai modellt kell alkotnia, abban számításokat végeznie, s a kapott eredményeket az eredeti probléma szempontjából értelmezve kell válaszolnia a felvetett kérdésekre. A jelöltnek az öt feladatból négyet kell kiválasztani, megoldani, és csak ez a négy értékelhető. A feladatok általában egy-két témakör ismeretanyagára támaszkodnak. A II. rész megoldásával elérhető összpontszám 64.
Értékelés
A javítási útmutató tartalmazza a feladatok részletes megoldásait, azok lehetséges változatait, az egyes megoldási lépésekre adható részpontszámokat.
Szóbeli vizsga
Tartalmi szerkezet
A szóbeli vizsgára legalább 20 tételt kell készíteni. A tételsor tartalmi arányai az írásbeli vizsga leírásánál meghatározott arányokat tükrözzék.
A tételek jellemzői
Az egyes tételek egy-egy témakörből kerülnek összeállításra. minden tétel megköveteli a tanulótól
| | egy definíció kimondását, |
| | egy tétel bizonyítását, |
| | egy feladat megoldását, |
| | valamint hogy mondjon példát az adott témakör alkalmazására a matematikán belül vagy azon kívül. |
A tételeket úgy kell összeállítani, hogy a nehézségük közel azonos legyen. Mivel a bizonyítandó állítások nehézsége különböző, ezért a kiválasztott feladat összetettségével, illetve nehézségi fokával lehet kiegyensúlyozni az adott tétel nehézségi szintjét.
Értékelés
A szóbeli vizsgán elérhető pontszám 35.
Az értékelés szempontjai:
PRÓBAÉRETTSÉGI
2003. május-június
MATEMATIKA
KÖZÉPSZINT
I. I. rész
1. Hány deciliter zsír van abban a fél literes tejeszacskóban, amelynek felirata szerint a zsírtartalma 2,8%?
2. Mennyi pontos értéke? (2 pont)
Írja fel a hatványt olyan alakban, hogy ne szerepeljen benne negatív kitevő! (2 pont)
3. Oldja meg a következő egyenlőtlenséget a valós számok halmazán:
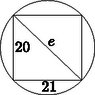
4. Legalább hány centiméter átmérőjű hengeres fatörzsből lehet kivágni olyan gerendát, amelynek keresztmetszete egy -es téglalap? Válaszát indokolja! (3 pont)
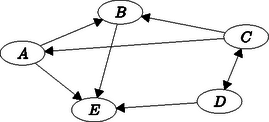
5. Egy iskolai bajnokságban 5 csapat körmérkőzést játszik. (Mindenki mindenkivel egyszer játszik.) Az ábra az eddig lejátszott mérkőzéseket mutatja. A nyíl mindig a győztes felé mutat. Döntetlen esetén az összekötő vonal mindkét végén nyíl van. A csapat győzelem esetén 2 pontot, döntetlen esetén 1 pontot kap, vereség esetén pedig nem kap pontot.
Kinek hány pontja van ebben a pillanatban? (2 pont)
Hány mérkőzés van még hátra? (2 pont)
6. Egy dobozban 5 piros golyó van. Hány fehér golyót tegyünk hozzá, hogy a fehér golyó húzásának valószínűsége 80% legyen? Válaszát indokolja! (4 pont)
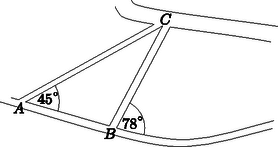
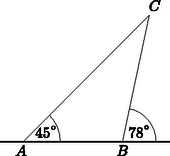
7. Az Alföldön térképészeti méréseket végeznek. Egy egyenes útszakasz pontjából is vezet egy út a -vel jelölt faluba, és az út távolabbi B pontjából is. Teodolittal (vízszintes és magassági szögek mérésére egyaránt alkalmas műszerrel) megmérik azt, hogy az első út -os, a második -os szöget zár be az úttal.
Mekkora szögben látszik a faluból az útszakasz a teodolitban? (2 pont)
8. Júniusban a 30 napból 12 olyan nap volt, amikor 3 mm-nél több, és 25 olyan, amikor 7 mm-nél kevesebb csapadék esett.
Hány olyan nap volt, amelyen 7 mm vagy annál több csapadék esett? (2 pont)
Hány olyan nap volt, amikor 3 mm-nél több, de 7 mm-nél kevesebb csapadék esett? (2 pont)
9. Mennyi a szám reciproka? Karikázza be a helyes válasz betűjelét! | |
(2 pont)
10. Állapítsa meg a valós számok halmazán értelmezett függvény zérushelyeit! (2 pont)
II. rész
A
11. Oldja meg a következő egyenleteket a valós számok halmazán:
. (6 pont)
. (6 pont)
12. Egy hajó a Csendes-óceán egy szigetéről elindulva 40 perc alatt 24 km-t haladt észak felé, majd az eredeti haladási irányhoz képest -ot nyugat felé fordulva 42 km/h egyenletes sebességgel folytatta útját.
(A sebességváltoztatáshoz szükséges idő elhanyagolható.)
Az indulás után 2,5 órával a hajó zátonyra futott.
Mennyi utat kell a mentőhajónak megtennie, ha a legrövidebb úton közelíti meg a hajót? (9 pont)
Milyen irányba kell útnak indítani (az északi irányhoz képest mekkora szögben) a szigetről a mentőhajót, hogy leghamarabb érkezzen a segítség? (A mentőhajó is a szigetről indul.) (3 pont)
13. Adott egy háromszög három csúcspontja a koordinátáival: , és . Számítsa ki a csúcsból induló súlyvonal és az csúcsból induló magasságvonal metszéspontjának koordinátáit! (12 pont)
II. rész
B
A 14., 15., 16. feladatok közül tetszés szerint választott kettőt kell megoldania.
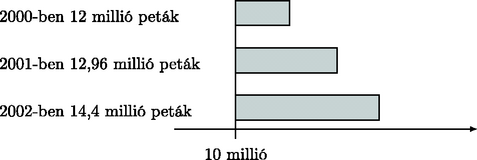
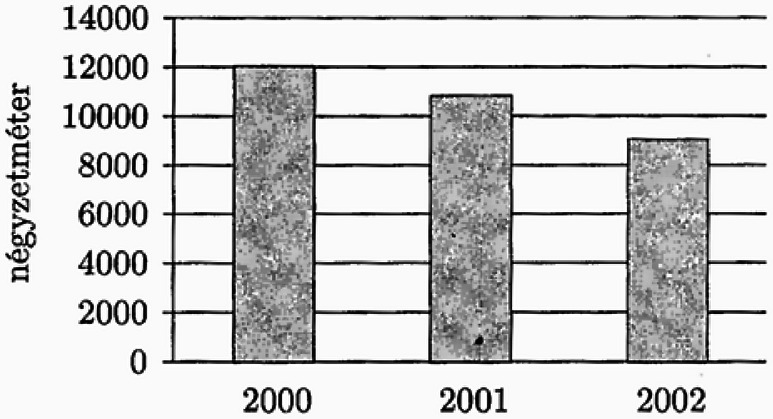
14. Bergengóciában az elmúlt 3 évben a kormány jelentése szerint kiemelt beruházás volt a bérlakások építése. Ezt az állítást az alábbi statisztikával támasztották alá.
Az egyes években a lakásépítésre fordított pénzösszegek:
Miért megtévesztő a fenti oszlopdiagram? (3 pont)
Valaki nem érzi meggyőzőnek ezt a statisztikát, és további adatokat keres. Kiderült, hogy 2000-ben új lakás építése átlagosan 1000 petákba került, 2001-ben az építési költségek 20%-kal emelkedtek, 2002-ben pedig az előző évi ár 1/3-ával növekedtek a költségek.
b) Hogyan változott a három év során az egyes években újonnan megépített bérlakások összalapterülete? Válaszát számításokkal indokolja! (8 pont)
c) Lehet-e az új adatok alapján olyan oszlopdiagramot készíteni, amelyből a kormány jelentésével ellentétes következtetés is levonható? Ha igen, akkor készítse el! (3 pont)
d) Több lakást építettek-e 2002-ben, mint 2001-ben? Válaszát indokolja! (3 pont)
15. Az egyén által érzékelt (szubjektív) hangerősség és a hangforrás valódi (objektív) hangerőssége közötti összefüggés: E=10⋅lg(I10-12), ahol I a wattm2-ben mért objektív hangerősség, E pedig a decibelben mért szubjektív hangerősség.
a) Az alig hallható suttogás objektív hangerőssége I=10-12wattm2, a hangszóróból áradó hangos zenéé pedig ennek 1 milliószorosa. Milyen erősségűnek érzik az emberek ezeknek a hangforrásoknak a hangját? (Mekkora a szubjektív hangerősség?) (8 pont)
b) Az 1000 Hz-es hangmagasságon süvítő repülőgép-motor hangosságát 130 decibelnek érzékeljük (3 méterről). Hányszorosa a motorzaj objektív hangerőssége a halk suttogásénak? (9 pont)
16. Egy háromlábú asztal lapja fél m2 területű szabályos háromszöglap.
a) Legalább mekkora az átmérője annak a kör alakú terítőnek, amelyik teljesen lefedi az asztallapot? (12 pont)
b) Az asztalra olyan kör alakú dísztálat helyezünk, amelyik egyik irányban sem nyúlik túl az asztal peremén. Legfeljebb hány cm lehet a tál átmérője? (5 pont)
JAVÍTÁSI ÚTMUTATÓ
Kérjük, hogy a dolgozatok javítását a javítási útmutató alapján végezze, a következők figyelembevételével:
| • | Az 1. javító tanár piros tollal javítson, és a tanári gyakorlatnak megfelelően jelölje a hibákat, hiányokat stb.
A 2. javító tanár zöld tollat használjon, és az első javítótól függetlenül a tanári gyakorlatnak megfelelően ő is jelölje a hibákat, hiányokat stb. |
| • | A feladatok mellett található üres négyzetek közül az 1. javító mindig az elsőt, a 2. javító mindig a másodikat töltse ki.
Kifogástalan megoldás esetén elég a megfelelő maximális pontszám beírása a szürke négyzetekbe.
Hiányos/hibás megoldás esetén kérjük az egyes részpontszámokat is írja rá a dolgozatra. |
| • | Kérjük, a dolgozat javítása után a füzetek belső borítóján található szürke táblázatot is töltse ki. |
| ∘ | Egyes feladatoknál több megoldás pontozását is megadtuk. Amennyiben azoktól eltérő megoldás születik, kérjük, hogy keresse meg ezen megoldásoknak az útmutató egyes részleteivel egyenértékű részeit és ennek alapján pontozzon. |
| ∘ | A pontozási útmutató pontjai további részpontokra nem bonthatók. Így, ha valamely részletre 3 pont adható, akkor az vagy 3 vagy 0 pontot jelent. |
| ∘ | Nyilvánvalóan helyes gondolatmenet és végeredmény esetén maximális pontszám adható akkor is, ha a leírás az útmutatóban szereplőnél kevésbé részletezett. |
| ∘ | Ha a megoldásban számolási hiba, pontatlanság van, akkor csak arra a részre nem jár pont, ahol a tanuló a hibát elkövette. Ha a hibás részeredménnyel helyes gondolatmenet alapján tovább dolgozik, akkor a következő részpontszámokat meg kell adni. |
| ∘ | Elvi hiba esetén, egy gondolati egységen belül a formálisan helyes matematikai lépésekre sem jár pont. Ha azonban az elhibázott részt egy újabb részkérdés követi, és a tanuló az elvi hibával kapott rossz eredménnyel mint kiinduló adattal helyesen számol tovább, akkor erre a részre kapja meg a maximális pontot. |
I. rész
1. feladat. 0,5 liter⋅0,028=0,014 liter. 2 pont
0,14 dl. 1 pont
(Az átváltás és a százalékszámítás sorrendje tetszőleges.)
2. feladat.
a) log232=5. 2 pont
b) (23)-5=3525=3532=(32)5=7,59375. 2 pont
(Bármilyen helyes megoldás elfogadható.)
3. feladat. 4-x<0. 1 pont
x>4. 1 pont
4. feladat. e2=212+202. 1 pont
e=29 cm.
(Mértékegység nélkül a 2 pontból 1 pont adható.) 2 pont
5. feladat.
a) A B C D E 24116
2 pont
(Ez a két pont akkor adható, ha legalább 4 válasz helyes. 1 pont akkor adható, ha 2 vagy 3 jó válasz van.)
b) 3 mérkőzés van még hátra. 2 pont
6. feladat. x legyen a fehér golyók száma.
5+x golyó van összesen.
xx+5=0,8.
(Az egyenlet felírásáért vagy jó gondolatmenetért.) 2 pont
x=0,8x+4,
0,2x=4,
x=20.
(A jó végeredményért.) 2 pont
7. feladat. A C csúcsnál lévő belső szög:
γ=78∘-45∘=33∘. 2 pont
8. feladat. a) 30-25=5 nap. 2 pont
b) 12+25-x=30,
x=7 nap.
(Indoklás és mértékegység nélkül is jár a pont.) 2 pont
9. feladat.
A b) válasz a jó. 2 pont
10. feladat. x2-2x-8=0 egyenlet gyökei lesznek a zérushelyek:
x1=-2. 1 pont
x2=4. 1 pont
(Nem szükséges a megoldóképlet részletezése.)
II./A rész
11. feladat.
a) 1. megoldás:
27⋅3x=3⋅32x. 1 pont
32x-9⋅3x=0. 1 pont
3x(3x-9)=0.
(Vagy a megoldóképlet alkalmazása.) 1 pont
3x=0, ennek nincs megoldása, 1 pont
vagy 3x=9, tehát x=2. 1 pont
(Ha 3x-ből nem számol x-et, akkor összesen 3 pont adható.)
Ellenőrzés. 1 pont
2. megoldás:
3x⋅33=32x+1. 1 pont
3x+3=32x+1. 2 pont
x+3=2x+1. 1 pont
x=2. 1 pont
Ellenőrzés. 1 pont
b) 3x+1=5-x2.
3x+1=5-x2. 1 pont
x2+3x-4=0. 1 pont
x1=1. 1 pont
x2=-4. 1 pont
Ellenőrzés: -4 hamis gyök. 1 pont
Az x=1 a megoldás. 1 pont
(Ha az értelmezési tartomány helyes felírásából derül ki, hogy melyik a jó megoldás, akkor is jár a 6 pont.)
12. feladat. a)
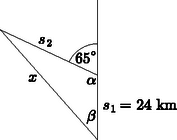 1 pont 1 pont
(A jó ábra 1 pontot ér, de a kifogástalan megoldás ábra nélkül is 12 pontos.)
Az elfordulás utáni út menetideje:
t2=150-40=110 perc,
t2=116 h.
(t2 megállapításáért.) 1 pont
Az elfordulás utáni út: s=v⋅t.
s2=116h⋅42kmh. 1 pont
s2=77 km. 1 pont
(s2 kiszámításáért összesen 2 pont.)
α=115∘. 1 pont
x2=242+772-2⋅24⋅77⋅cos115∘.
(A koszinusz tétel helyes felírásáért összesen 2 pont.) 2 pont
x2=8066,98,
x=89,8 km. 2 pont
(Mértékegység nélkül csak 1 pont jár. Nem számít hibának, ha mértékegységet csak a végeredményben tüntet fel a vizsgázó, amennyiben közben helyesen számol.)
b) sinβsinα=s2x. 1 pont
sinβ=sin115∘⋅7789,8=0,7771. 1 pont
β=50,99∘≈51∘. 1 pont
13. feladat. A magasságvonal egyenlete:
n=BC→(-8;4). 2 pont
n(-2;1),
A(-4;-4),
-2x+y=4. 3 pont
(A magasságvonal egyenletéért 5 pont.)
A súlyvonal egyenlete:
F(0;0). 1 pont
FC→(-4;8). 1 pont
n(8;4)=(2;1). 1 pont
2x+y=0. 2 pont
(A súlyvonal egyenletéért 5 pont.)
A metszéspontjuk az egyenletrendszer megoldása:
P(-1;2).
(A metszéspont kiszámításáért 2 pont.) 2 pont
(Ha egy pontos rajzról leolvassa a jó végeredményt, akkor összesen 3 pont adható.)
II./B rész
Az alábbi három feladat (14‐16.) közül tetszés szerint választott kettőt kellett megoldani és kettőt kell értékelni!
14. feladat. a) Az oszlopok hossza nem arányos az ábrázolt mennyiségekkel, így az ábra jóval nagyobb növekedést sugall, mint a valóság. 3 pont
b) 2000: 1000 peták/m2,
b)2001: 1200 peták/m2, 1 pont
b)2002: 1600 peták/m2. 1 pont
2000: 1,2⋅107103=12000m2 új lakás épült. 1 pont
2001: 1,296⋅1071200=10800m2 új lakás épült. 1 pont
2002: 1,44⋅1071600=9000m2 új lakás épült. 1 pont
Tehát az egy év alatt felépített bérlakások összes alapterülete évről évre csökkent. 3 pont
c)
(79,42)(0,0) (-12,23)(0,0)négyzetméter (8,5)(0,0)00000 (8,10)(0,0)02000 (8,15)(0,0)04000 (8,20)(0,0)06000 (8,25)(0,0)08000 (8,30)(0,0)10000 (8,35)(0,0)12000 (8,40)(0,0)14000 (15,5)0,1)35 (14,5)1,0)61 (14,10)1,0)61 (14,15)1,0)61 (14,20)1,0)61 (14,25)1,0)61 (14,30)1,0)61 (14,35)1,0)61 (14,40)1,0)61 (21,5) (41,5) (61,5) (22,0)2000 (42,0)2001 (62,0)2002 3 pont
d) A megadott adatokból nem állapítható meg, mert nem tudjuk egy-egy lakás alapterületét (ami igen változó lehet). 3 pont
15. feladat. a) E1=10⋅lg10-1210-12.
(A képlet értelmezéséért.) 2 pont
E1=10⋅lg1=0 decibel.
(Mértékegység nélkül 1 pont.) 2 pont
E2=10⋅lg10-610-12.
(A képlet értelmezéséért.) 2 pont
E2=10⋅lg106=60 decibel.
(Mértékegység nélkül 1 pont.) 2 pont
b) I=10-12Wm2.
Legyen Em a motor szubjektív hangerőssége,
Im az objektív hangerőssége.
Em=130 decibel.
(Az adat értelmezéséért.) 1 pont
130=10⋅lgIm10-12.
(Az egyenlet felírásáért.) 3 pont
13=lgIm10-12. 1 pont
1013=Im10-12.
(A logaritmus értelmezéséért.) 3 pont
Tehát a motorzaj objektív hangerőssége a halk suttogásénak 1013-szorosa. 1 pont
16. feladat. a) T=a⋅m2, ahol m=a32, tehát T=a234,
a234=0,5. 2 pont
a=23≈1,07. 2 pont
A köré írható kör átmérőjét keressük. 1 pont
A sugár a súlyvonal 2/3-ad része. 1 pont
R=a32⋅23. 2 pont
R=a3=233. 1 pont
Legalább 125 cm átmérőjű terítő kell.
(124 cm is elfogadható. Ha kerekítés miatt ennél kisebb értéket kap, akkor ez a pont nem jár.) 1 pont
b)
1. megoldás:
A beírt kör sugarát keressük, ami a körülírt kör sugarának a fele.
r=R2. 5 pont
Tehát a tál átmérője: 0,62m= 1 pont
=62cm. 1 pont
2. megoldás:
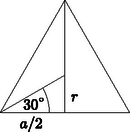 1 pont 1 pont
tg30∘=ra/2. 2 pont
r=a2⋅tg30∘. 1 pont
r=0,31. 1 pont
d=0,62 m. 1 pont
d=62 cm. 1 pont
PRÓBAÉRETTSÉGI
2003. május-június
MATEMATIKA
EMELT SZINT I. rész
1. Adott két egyenes egyenlete:
a) Határozza meg az egyenesek metszéspontjának koordinátáit! (2 pont)
b) Számítsa ki a két egyenes hajlásszögét! (5 pont)
c) Mekkora távolságra van az origó az e egyenestől? (5 pont)
2. Tekintse az alábbi táblázatot!
| A nők számaEzer nőre jutóA nők számaEzer nőre jutóKorcsoport(ezer főben)szülések száma(ezer főben)szülések száma193019301995199515‐19253040,9417033,620‐24217158,5372113,925‐29181151,8331110,330‐34173110,7305050,235‐39194074,8382017,240‐44205015,74182 |
a) Hány gyerek született összesen 1930-ban és hány született 1995-ben? (4 pont)
b) Hány százalékkal nőtt vagy csökkent a szülések száma 1930 és 1995 között 1930-hoz képest? (2 pont)
c) Hány százalékkal nőtt vagy csökkent az ezer nőre jutó szülések száma 1930 és 1995 között 1930-hoz képest? (4 pont)
d) Egy 1995 szilveszterén készült TV-interjúhoz véletlenszerűen választottak ki egy riportalanyt a 20‐24 év közötti nő lakosok közül. Mennyi annak a valószínűsége, hogy a kiválasztott nő szült abban az évben? Válaszát indokolja! (3 pont)
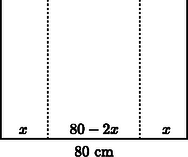
3. Egy 80 cm széles bádoglemez két párhuzamos szélének egyforma felhajtásával téglalap keresztmetszetű vízlevezetőt készítünk úgy, hogy a víz a lehető leggyorsabban folyjon át rajta. (Ez akkor következik be, ha a keresztmetszetének a területe a lehető legnagyobb.)
a) Határozza meg a felhajtott rész szélességét! (11 pont)
b) Határozza meg, mekkora a lehető legnagyobb keresztmetszet területe! (2 pont)
4. Egy repülőgépnek 2400 km utat kellett megtennie. Az út első harmadában a rossz időjárási viszonyok miatt az eredetileg tervezett sebességét 25%-kal csökkentette.
a) Az eredetileg tervezetthez képest hány százalékkal kellene növelnie a sebességét az út hátralevő részében, ha késés nélkül szeretne leszállni? (6 pont)
b) Sajnos az időjárás nem javult lényegesen, így a gép az út második részében az eredetileg tervezett sebességénél 160kmh-val kisebb sebességgel tudott haladni. Mekkora volt az eredetileg tervezett átlagsebessége és menetideje, ha így egy óra késéssel érkezett a célállomásra? (7 pont)
II. rész
Az alábbi öt feladat (5.‐9.) közül tetszés szerint választott négyet kell megoldania!
5. Oldja meg az alábbi egyenletet a valós számpárok halmazán: | 16x2-(8cosy)x+1=0.(16 pont) |
6. a) Igazolja, hogy az n3-n kifejezés osztható hattal, ha n természetes szám! (5 pont)
b) Melyek azok a k egész számok, amelyekre a k2-3k kifejezés egy prímszám négyzetével egyenlő? (11 pont)
7. a) Legalább hány tanuló jár abba az iskolába, ahol a tanulók megkérdezése nélkül is tudjuk, hogy biztos van három olyan diák, aki ugyanazon a napon ünnepli a születésnapját? (4 pont)
Az iskolában 3 különböző szakkör működik: dráma, fotó, népi tánc. Egy 22 fős osztály minden tanulója legalább az egyik szakkörön részt vesz. Az osztályfőnök számítógépes nyilvántartást vezet a tanulókról, amelyben egy számhármassal jellemzi azt, hogy ki melyik szakkörre jár. Az első szám a dráma, a második a fotó, a harmadik a népi táncra vonatkozik. Egyes jelzi, ha valaki részt vesz a szakkör munkájában, nulla, ha nem. Pl. ha egy diák a drámaszakkörre jár, a fotóra nem és a néptáncra igen, az azt jelenti, hogy az ő kódszáma: 101
b) Hány különböző számhármas szerepelhet a tanár nyilvántartásában? (3 pont)
c) Mutassa meg, hogy van legalább 4 olyan tanuló, aki pontosan ugyanazokat a szakköröket látogatja! (6 pont)
d) A 22 tanulóból pontosan két szakkört látogat 16 tanuló, és van 3 olyan, aki mindegyikre jár. Hány tanuló jár pontosan egy szakkörre? (3 pont)
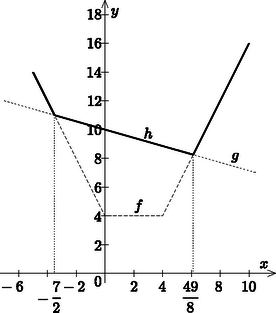
8. Legyen adott a valós számok halmazán értelmezett | f(x)=|x|+|x-4|ésg(x)=-27x+10 |
függvény.
a) Mely x értékek esetén teljesül, hogy f(x)=g(x)? (9 pont)
b) Értelmezzük a h függvényt a [-5;10] intervallumon a következőképpen: | h(x)={f(x),ha f(x)≥g(x)g(x),ha g(x)≥f(x). |
Ábrázolja az f, a g és a h függvényeket a [-5;10] intervallumon, közös koordinátarendszerben! (7 pont)
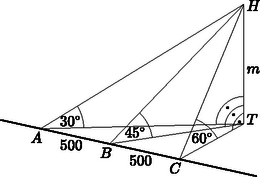
9. Egy vízszintes egyenes úton haladunk. Az út bal oldalán a hegy tetején egy kilátót veszünk észre. Ennek a kilátónak a tetejét az útról 30∘-os emelkedési szögben látjuk. Fél km-t továbbhaladva az emelkedési szög már 45∘-os. Újabb 500 méter megtétele után már 60∘-os az emelkedési szög. Milyen magasan van az úthoz képest a kilátó teteje? Készítsen ábrát! (16 pont)
JAVÍTÁSI ÚTMUTATÓ I. rész
1. feladat. a) y=3x-2.
x+3(3x-2)=-6.
x=0, y=-2.
M(0;-2). 2 pont
(Bármilyen rendezéssel eljuthat az x és y értékéig. Pontos rajz és annak leolvasása esetén 1 pont adható.)
b) ne(3;-1). 1 pont
nf(1;3). 1 pont
|ne|=32+(-1)2=10,
|nf|=12+32=10.
(A vektorok hosszának meghatározásáért.) 1 pont
3-3=10⋅10⋅cosα.
(A skalárszorzat kétféle felírásáért.) 1 pont
cosα=0, α=90∘. 1 pont
(Ha a normálvektorok vagy az irányvektorok skaláris szorzatából vagy a meredekségekből veszi észre, hogy a két egyenes egymásra merőleges, természetesen akkor is jár az 5 pont. Ha a pontos rajzról olvassa le a szöget, akkor 1 pont jár.)
c) Az origón átmenő, az e egyenesre merőleges egyenes egyenlete: x+3y=0. 2 pont
Ennek metszéspontja az e egyenessel: T(35;-15). 2 pont
Ennek távolsága az origótól: 105≈0,63. 1 pont
(Ha a pont‐egyenes távolságképletével vagy más módon számol, akkor is jár az 5 pont.)
2. feladat. a) Súlyozott számtani átlaggal kell számolni.
1930:
253⋅40,9+217⋅158,5+181⋅151,8+173⋅110,7+194⋅74,8+205⋅15,7=109098,8. 1 pont
Tehát 1930-ban 109 099 gyerek született. 1 pont
1995:
417⋅33,6+372⋅113,9+331⋅110,3+305⋅50,2+382⋅17,2+418⋅2=115608,7. 1 pont
Tehát 1995-ben 115609 gyerek született. 1 pont
b) A születések számának változása: | 115609-109099109099⋅100≈6. | 1 pont |
Tehát 6%-os a növekedés. 1 pont
c) Az 1000 nőre jutó születések számának változása:
1930-ban 1000 nőre 109098,81223=89,2 szülés jutott. 1 pont
1995-ben 1000 nőre 1156092225=52,0 szülés jutott. 1 pont
A második adat az elsőnek 100⋅52,089,2=58,3%-a. 1 pont
Tehát 41,7%-os a csökkenés. 1 pont
d) Az adott korosztályba (20‐24) tartozó nőknek 113,9 ezreléke szült gyereket, ami 11,39%-os valószínűséget jelent.
(Az indoklás nélküli válaszért nem jár pont, ha nem teljes az indoklás, akkor kevesebb is adható.) 3 pont
3. feladat. a) Legyen a felhajtott rész szélessége x.
Többféle megoldást is megadunk, ezért alapvetően a következők szerint bontjuk az a) rész pontszámát:
A függvény felírásáért. 2 pont
A szélsőérték helyének jó meghatározásáért.
(Ha a függvény felírása után a maximum helyét a lépések részletezése nélkül állapítja meg, akkor is kapja meg a teljes pontszámot.) 8 pont
Mértékegységgel megadott válaszért. 1 pont
1. megoldás:
A keresztmetszet területe, amelynek a maximumát keressük:
T(x)=x⋅(80-2x). 2 pont
T(x)=-2x2+80x. 2 pont
Teljes négyzetté alakítva: T(x)=-2(x-20)2+800. 3 pont
A negatív előjel miatt a függvénynek maximuma van. 2 pont
A maximum helye: xmax=20. 1 pont
Tehát a felhajtott rész szélessége 20 cm.
(A mértékegység helyes feltüntetéséért.) 1 pont
2. megoldás:
A keresztmetszet területe, amelynek a maximumát keressük:
T(x)=x⋅(80-2x). 2 pont
T(x)=-2x2+80x. 2 pont
Deriváltja: T'(x)=-4x+80. 2 pont
T'(x)=0. 1 pont
-4x+80=0. 1 pont
x=20. 1 pont
T''(20)=-4<0, azaz maximuma van. 1 pont
Tehát a felhajtott rész szélessége 20 cm.
(A mértékegység helyes feltüntetéséért.) 1 pont
3. megoldás:
Számtani és mértani közép segítségével:
(80-2x)⋅x maximumát keressük. 2 pont
Nézzük a függvény kétszeresét, annak ugyanott van a maximuma:
(80-2x)⋅2x≤[(80-2x)+2x2]2. 3 pont
(80-2x)⋅2x≤402=1600. 1 pont
Maximum ott van, ahol a két tényező egyenlő: 2 pont
80-2x=2x. 1 pont
x=20. 1 pont
Tehát a felhajtott rész szélessége 20 cm.
(A mértékegység helyes feltüntetéséért.) 1 pont
4. megoldás:
T(x)=x⋅(80-2x). 2 pont
A kapott konkáv parabola 2 pont
zérushelyei: 0 és 40. 3 pont
A maximum helye tehát x=20. 3 pont
Tehát a felhajtott rész szélessége 20 cm.
(A mértékegység helyes feltüntetéséért.) 1 pont
b) Értéke: Tmax=800cm2. 2 pont
4. feladat. a) Az eredetileg tervezett sebesség: v.
Az eredetileg tervezett menetidő: t=2400v.
Az út első harmada: 800 km.
Ezen a részen az átlagsebessége: 0,75v.
A menetidő: t1=8000,75v.
Az út másik része: 1600 km.
Ezen a részen az átlagsebessége: x.
A menetidő: t2=1600x.
t=t1+t2.
2400v=8000,75v+1600x.
(Az egyenlet felírásáért.) 3 pont
x=1,2v.
(Az egyenlet megoldásáért.) 2 pont
Tehát 20%-os sebességnövelésre van szükség.
(A % megállapításáért.) 1 pont
b) A sebesség 160kmh-val csökken, ezért az út második részén az átlagsebesség: v-160.
A menetidő: t2'=1600v-160.
t+1=t1+t2'.
2400v+1=8000,75v+1600v-160.
(Az egyenlet felírásáért.) 3 pont
Az egyenletrendezés után a következő másodfokú egyenletet kapjuk:
0,75v2-320v-160000=0.
(Az egyenlet rendezéséért.) 2 pont
Ennek pozitív gyöke: v=722,1.
Tehát az eredeti sebesség 722,1 km/h.
(A gyök kiszámításáért és értelmezéséért.) 1 pont
A tervezett menetidő: t=2400722,1≈3,32.
A tervezett menetidő 3,32 óra.
(A menetidő meghatározásáért.) 1 pont
(Ha az eredeti sebesség helyett az a)-ban kiszámolt értéket csökkenti 160-nal (szövegértési hiba) és ezzel az értékkel mindent jól kiszámol, akkor 5 pont jár.)
II. rész
Az alábbi öt feladat (5.‐9.) közül a tanulónak tetszés szerint választott négyet kellett megoldani és négyet kell értékelni!
5. feladat.
1. megoldás:
A másodfokú egyenletnek akkor és csak akkor van megoldása, ha a diszkrimináns nemnegatív:
64cos2y-64≥0. 3 pont
cos2y≥1. 1 pont
Ez csak akkor teljesülhet, ha cosy=±1.
(Ha csak az egyiket írja, akkor 1 pont jár.) 3 pont
(A cosy lehetséges értékeinek a meghatározásáért összesen 7 pont.)
Ha cosy=1, akkor y=2kπ, 1 pont
ahol k∈Z. 1 pont
16x2-8x+1=0. 1 pont
x=14. 1 pont
Az egyik megoldás: (14;2kπ), ahol k∈Z.
(Az egyik gyöksorozat felírásáért összesen 4 pont.)
Ha cosy=-1, akkor y=π+2kπ, 1 pont
ahol k∈Z. 1 pont
16x2+8x+1=0. 1 pont
x=-14. 1 pont
A másik megoldás: (-14;π+2kπ), ahol k∈Z.
(A másik gyöksorozat felírásáért összesen 4 pont.)
Ellenőrzés: 1 pont
‐ ekvivalens átalakításokat hajtottunk végre, tehát a kapott gyökök kielégítik az egyenletet.
‐ behelyettesítéssel.
(Ha csak az egyik gyöksorozatot találja meg és azt ellenőrzi, akkor is megkapja az 1 pontot.)
2. megoldás:
A megoldóképletet alkalmazva: | x=8cosy±64cos2y-6432. | 2 pont |
Ez akkor értelmezhető, ha siny=0. 1 pont
Ekkor cosy=±1.
(Ha csak az egyiket írja, akkor 1 pont jár.) 3 pont
(Eddig összesen 7 pont.)
Innen kezdve ld. az 1. megoldást.
6. feladat.
a) n3-n=n(n2-1)= 1 pont
=n(n+1)(n-1). 1 pont
Három szomszédos szám közül az egyik biztosan páros, ezért osztható 2-vel, és 1 pont
van közöttük biztosan hárommal osztható is, 1 pont
ezért a szorzatuk osztható 6-tal. 1 pont
b) 1. megoldás:
A feltétel szerint k2-3k=p2, ahol p prímszám.
A fenti egyenlet k⋅(k-3)=p2 alakban írható fel.
(Átírás szorzat alakba.) 2 pont
A jobboldal: 1⋅p2, (1) 1 pont
vagy p⋅p, (2) 1 pont
vagy (-1)⋅(-p2) (3) lehet. 1 pont
(Az esetek szétválasztásáért összesen 3 pont jár.)
(1) Ha k=1 és k-3=p2, akkor p2=-2, ami nem lehet. 1 pont
Ha k-3=1, és k=p2, akkor k=4, tehát p2=4, azaz p=2. 1 pont
(Az (1) eset vizsgálatáért összesen 2 pont jár.)
(2) k=k-3, ami nem lehetséges.
(A (2) eset vizsgálatáért 1 pont jár.) 1 pont
(3) Ha k=-1 és k-3=-p2, akkor p2=4, tehát p=2. 1 pont
Ha k-3=-1 és k=-p2, akkor k=2, tehát p2=-2, ami nem lehet. 1 pont
(A (3) eset vizsgálatáért összesen 2 pont jár.)
A feladat feltételeinek a k=4 és a k=-1 felel meg. 1 pont
Ez esetekben lesz a k2-3k kifejezés egy prímszám, a 2 négyzetével egyenlő.
2. megoldás:
A feltétel szerint k2-3k=p2, ahol p prímszám.
k2-3k kifejezés mindenképpen páros, mert 2 pont
‐ ha k páros, akkor két páros szám különbsége páros, 2 pont
‐ ha k páratlan, akkor két páratlan szám különbsége szintén páros. 2 pont
Így tehát p2 is páros.
Ha p2 páros, akkor p csak 2 lehet. 2 pont
Így k2-3k=4, 1 pont
ahonnan k=4, 1 pont
vagy k=-1. 1 pont
7. feladat a) 366 különböző születésnap lehet.
(365 nap esetén is jár a pont.) 1 pont
Ha minden napra legfeljebb 2 születésnap esik, akkor legfeljebb 366⋅2=732 tanulója van az iskolának.
(365 nap esetén 730.) 1 pont
A 733. tanulónak már biztosan van 2 azonos napon született társa.
(365 nap esetén 731.) 1 pont
Tehát legalább 733-an járnak az iskolába.
(365 nap esetén 731.) 1 pont
(Ha nincs részletes szöveges magyarázat, de a gondolatmenet egyértelműen jó, akkor is megadható a 4 pont.)
b) Mindhárom helyre 2 lehetőségünk van, így 2⋅2⋅2=8 lehetséges számhármas van. 1 pont
A 000 nem lehet, 1 pont
ezért összesen 7 marad. 1 pont
(Ha módszeresen összeszámlálja a lehetséges eseteket, akkor az 3 pont. Ha az összeszámlálásban téved, akkor legfeljebb 1 pont adható.)
c) 7 különböző lehetőség van. 1 pont
Ha mindegyikbe 3 tanuló tartozik, akkor 7⋅3=21 tanuló lenne. 3 pont
De 22 van, ezért valamelyik csoportban 4 tanuló lesz.
(Ez halmazábrán is megmutatható.) 2 pont
d) 22=16+3+x. 2 pont
x=3. 1 pont
8. feladat. a)
Ha x<0, akkor:
x=-72, és ez benne van a vizsgált intervallumban.
(Szöveges indoklás helyett más jelölés is megfelelő.) 1 pont
Ha 0≤x≤4, akkor: 1 pont
x=21, de ez nincs benne a vizsgált intervallumban. 1 pont
Ha x≥4, akkor: 1 pont
x=498, és ez benne van a vizsgált intervallumban. 1 pont
(A három eset vizsgálatáért 3‐3 pont jár.)
b) f ábrázolása 3 pont
g ábrázolása 1 pont
h ábrázolása 3 pont
9. feladat. Az első pont A, a második B, a harmadik C, a kilátó teteje H. 3 pont
(A térbeli viszonyok jó elképzelését tükröző ábráért az adatok feltüntetése nélkül is 3 pont adható.)
A hegy magasságát jelölje a HT=m szakasz.
Az ATH, BTH és CTH derékszögű háromszögekből rendre:
AT=m3. 1 pont
BT=m. 1 pont
CT=m3. 1 pont
(AT; BT és CT ugyanazzal a paraméterrel való kifejezéséért 1‐1 pont jár.)
Ha ABT szöget α-val jelöljük, akkor a TBC∢=180∘-α.
Az ABT és TBC háromszögekben a koszinusztételt az AT illetve a BT oldalakra felírva:
(1) 3m2=5002+m2-2⋅500⋅m⋅cosα. 2 pont
(2) m23=5002+m2-2⋅500⋅m⋅cos(180∘-α). 2 pont
(2) m23=5002+m2+2⋅500⋅m⋅cosα. 2 pont
(Vagy pl. az ACT háromszögben a CT és az ABT-ben a BT oldalakra felírva a koszinusztételt: 3‐3 pont.)
(A kétismeretlenes egyenletrendszer felírásáért összesen 6 pont.)
Az (1) és (2) egyenleteket összeadva: | m2(3+13)=2(5002+m2). | 2 pont |
A hegy magassága körülbelül 612 méter. 1 pont
(A kapott végeredményhez még a megfigyelő magasságát kellene hozzáadnunk, de ettől a megoldás értékelésénél eltekinthetünk.)
|
 PDF | MathML
PDF | MathML 
 1 pont
1 pont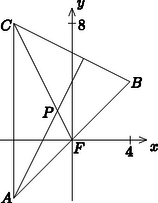
 1 pont
1 pont