Cím:	A 2002-2003. évi Országos Középiskolai Matematikai Tanulmányi Verseny feladatai
Füzet:	2003/november, 459 - 461. oldal	PDF  |  MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. II. kategória: Általános matematika tantervű gimnáziumok   Első (iskolai) forduló   1. Hagyjunk el az $\mathrm{1,2,3,}\text{...}\mathrm{,24}$ számok közül néhányat úgy, hogy a megmaradtak szorzata a lehető legnagyobb köbszám legyen. Legalább hány számot kell elhagynunk?   2. Bizonyítsuk be, hogy ha $n$ 1-nél nagyobb egész, akkor $\begin{array}{c}{\displaystyle S=\left(1+\frac{1}{3}\right)\cdot \left(1+\frac{1}{8}\right)\cdot \text{...}\cdot \left(1+\frac{1}{n^2-1}\right)<2.}\end{array}$   3. 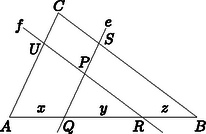Az $ABC$ háromszög $AC$ oldalával párhuzamos $e$ egyenes és a $BC$ oldalával párhuzamos $f$ egyenes felezik a háromszög területét; $e$ és $f$ a $P$ pontban metszik egymást; az $e$ egyenes az $AB$ oldalt a $Q$ pontban, $f$ az $R$ pontban metszi. Határozzuk meg az $ABC$ és a $QPR$ háromszögek területének az arányát.     4. Állítsuk elő az $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_n\mathrm{,}\text{...}$ sorozat $a_n$ tagját csupán $n$ felhasználásával, ha tudjuk, hogy $a_1=1$ és $a_{n+1}=n{a}_n+n^2-n-1$ ($n$ pozitív egész).   5. Adott a $k$ kör és annak egy $AB$ átmérője. A $k_1$ és $k_2$ körök az $AB$ által meghatározott egyik félkör belsejében helyezkednek el; $k_1$ a $k$ kört a $P$ pontban, $AB$-t a $Q$ pontban érinti; ugyanígy $k_2$ a $k$ kört az $S$, az $AB$-t pedig az $R$ pontban érinti. Bizonyítsuk be, hogy a $PQRS$ négyszög húrnégyszög.   Második forduló   1. Az $ABCD$ paralelogramma egyik szöge ${30}^{\circ }$-os, $AB=a$, $BC=b$. A paralelogramma csúcsaiban síkjára merőleges, egyirányú félegyeneseket állítunk; az $A$-ban, illetve $C$-ben állított merőlegeseken úgy jelöljük ki az $A\text{'}$, illetve $C\text{'}$ pontokat, hogy $AA\text{'}=a$, $CC\text{'}=b$ teljesüljön. Az $A\text{'}C\text{'}$ egyenest tartalmazó sík a $B$-ben, illetve a $D$-ben állított merőleges félegyeneseket a $B\text{'}$, illetve a $D\text{'}$ pontokban metszi. Mekkora annak a síklapokkal határolt konvex testnek a térfogata, amelynek csúcsai $A$, $B$, $C$, $D$, $A\text{'}$, $B\text{'}$, $C\text{'}$, $D\text{'}$?   2. Legyenek $n$ és $a$ pozitív egészek, $a>1$. Bizonyítsuk be, hogy $a^{5n}+a^n+1$ nem lehet prímszám.   3. Egy háromszög oldalai: $a$, $b$, $c$, a velük szemközti szögek rendre $\alpha$, $\beta$, $\gamma$; a köré írt kör sugara $R$. Mekkorák a háromszög szögei, ha a fenti adatok között az $\frac{a\text{cos}\alpha +b\text{cos}\beta +c\text{cos}\gamma }{a\text{sin}\beta +b\text{sin}\gamma +c\text{sin}\alpha }=\frac{a+b+c}{9R}$ összefüggés áll fenn?   4. Az $x$, $y$, $z$ nemnegatív valós számok kielégítik az $x^2+y^2+z^2+x+2y+3z=\frac{13}{4}$ egyenletet. A) Mekkora az $x+y+z$ összeg maximuma? B) Bizonyítsuk be, hogy $x+y+z\ge \frac{\sqrt[]{22}-3}{2}$.   Harmadik (döntő) forduló   1. Az $ABC$ háromszög $AB$ oldalát kívülről érintő hozzáírt kör az $AB$-t a $C\text{'}$ pontban, a $BC$ oldalt kívülről érintő hozzáírt kör $BC$-t az $A\text{'}$ pontban és a $CA$ oldalt kívülről érintő hozzáírt kör $CA$-t a $B\text{'}$ pontban érinti. Az $A$, $B$, $C$ csúcsokból induló magasságok felezőpontjai rendre $X$, $Y$, $Z$. Bizonyítsuk be, hogy az $XA\text{'}$, $YB\text{'}$ és a $ZC\text{'}$ egyenesek átmennek a beírt kör középpontján.   2. Legyen $n>2$ egész szám. Jelöljük $a_n$-nel a legnagyobb olyan $n$-jegyű pozitív egész számot, amely nem állítható elő sem két négyzetszám különbségeként, sem pedig két négyzetszám összegeként. a) Adjuk meg $a_n$-et $n$ függvényében. b) Határozzuk meg azt a legkisebb $n$ értéket, amelyre $a_n$ jegyeinek a négyzetösszege négyzetszám.   3. Egy $ABCD$ szabályos tetraéder három lapja fehér, a negyedik, a $D$ csúccsal szemközti lapja fekete, és a tetraéder az $S$ síkon ezen a fekete lapján áll. A tetraédert gördíthetjük, azaz az $S$ síkon egyik éle körül elforgatva az erre az élre illeszkedő másik lapja fekszik rá az $S$ síkra. Néhány gördítés után a tetraéder a kiindulási helyén áll. Bizonyítsuk be, hogy ekkor az $S$ síkon levő lapja nem lehet fehér.   III. kategória: Speciális matematika tantervű gimnáziumok   Első (iskolai) forduló   1. Jelölje $V$ egy téglatest térfogatának mérőszámát köbcentiméterben mérve, $F$ pedig a felszínének mérőszámát négyzetcentiméterben mérve. Mennyi a lehető legkisebb térfogata egy olyan téglatestnek, amelyre $V=10F$?   2. A $H$ háromszöget daraboljuk fel a $H_1\mathrm{,}{H}_2\mathrm{,}\text{...}\mathrm{,}{H}_n$ részháromszögekre. Jelölje $\varrho$, illetve a ${\varrho }_i$ a $H$, illetve $H_i$ háromszög beírt körének a sugarát. Mutassuk meg, hogy $\varrho \le {\varrho }_1+{\varrho }_2+\text{...}+{\varrho }_n$.   3. Az $ABC$ háromszög $A$ csúcsából a $B$ és $C$ csúcsokból induló belső szögfelezőkre bocsátott merőlegesek talppontjai legyenek $A_1$ és $A_2$. Ugyanígy értelmezzük a $B_1$ és $B_2$, valamint $C_1$ és $C_2$ talppontokat is. Bizonyítsuk be, hogy az $A_1{A}_2+B_1{B}_2+C_1{C}_2$ összeg egyenlő a háromszög félkerületével.   4. Két zsákban piros és fehér golyók vannak. A kisebbikben 20 piros és 20 fehér, a nagyobbikban 1005 piros és 995 fehér golyó található. Tetszésünk szerint kiválasztjuk az egyik zsákot, ebből kihúzunk egy golyót, megnézzük és félretesszük, majd ismét tetszésünk szerint kiválasztunk a két zsák közül egyet, és kihúzunk belőle egy golyót. Milyen stratégiával érhetjük el, hogy a két kihúzott golyóból a lehető legnagyobb valószínűséggel legyen legalább az egyik piros?   5. Megadható-e 2002 különböző pozitív egész úgy, hogy közülük bármelyik két különbözőnek a különbsége abszolút értékben megegyezzék a legnagyobb közös osztójukkal?   Második (döntő) forduló   1. A sík egy $H$ ponthalmazát nevezzük szépnek, ha $H$ bármely háromelemű részhalmaza tengelyesen szimmetrikus. Igazoljuk az alábbi két állítást: a) Egy szép halmaz nem feltétlenül tengelyesen szimmetrikus. b) Egy 2003 elemű szép halmaz pontjai szükségképpen egy egyenesre esnek.   2. Egy adott 2003-szög minden csúcsát pirosra, kékre vagy zöldre színezzük úgy, hogy szomszédos csúcsoknak nem lehet azonos a színe. Hányféleképpen tehetjük ezt meg?   3. Legyen $t$ rögzített pozitív egész, és jelölje $f_t\left(n\right)$ azoknak a $k$ pozitív egészeknek a számát, amelyekre $1\le k\le n$ és $\left(\genfrac{}{}{0ex}{}{k}{t}\right)$ páratlan. (Ha $1\le k<t$, akkor $\left(\genfrac{}{}{0ex}{}{k}{t}\right)=0$.) Bizonyítsuk be, hogy ha $n$ elég nagy kettőhatvány, akkor $\begin{array}{c}{\displaystyle \frac{f_t\left(n\right)}{n}=\frac{1}{2^r}\mathrm{,}}\end{array}$ ahol az $r$ egész szám csak a $t$-től függ, az $n$-től nem.