Cím: A 2002-2003. évi Arany Dániel Matematikai Tanulóverseny feladatai
Füzet: 2003/november, 455 - 459. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.


KEZDŐK
 
Első forduló
 

Mindhárom kategória
 

1. Oldja meg a következő egyenelőtlenséget a valós számok halmazán:
|x+1x|>p,
ahol p valós paramétert jelent!  (6 pont)
 
2. Határozza meg azokat a (pozitív) p prímszámokat, amelyekre p2+12p+2 is prímszám!  (6 pont)
 
3. Igazolja, hogy ha egy téglatest összes élének mérőszámát összeadjuk és ezt az összeget a felszínének a mérőszámával megszorozzuk, akkor a térfogata mérőszámának negyvenszeresénél nagyobb értéket kapunk!  (8 pont)
 
4. Kössük össze az ABCD négyzet A csúcsát a négyzet belsejében fekvő E ponttal, amelyre AB=BE. Jelölje a CE szakasz felezőmerőlegesének és az AE egyenesnek a metszéspontját P. Igazolja, hogy P illeszkedik a négyzet körülírt körére!  (10 pont)
 
5. Igazolja a következő egyenlőtlenséget (ahol a nevező mindig 10-zel nő)!
13+113+123+...+12003>23(10 pont)

 
Második (döntő) forduló
 

II. kategória: Általános matematika tantervű gimnáziumok
 

1. Mennyi az alábbi kifejezés legkisebb értéke, ha x és y valós számok:
2x2-xy+y2+2x+3y.

 
2. Az ABC háromszög AB oldalával párhuzamos középvonalának egyenesét az A csúcsból kiinduló belső szögfelezője az M, a B csúcsból kiinduló belső szögfelezője az N pontban metszi. Ugyanígy kapjuk a másik két oldalból kiindulva a KL és PQ szakaszt. Mutassa meg, hogy:
2(MN+KL+PQ)=AB+AC+BC.

 
3. Bizonyítsa be, hogy van olyan szám, amely a tízes számrendszerben 987654321-re végződik és osztható 2003-mal!
 
III. kategória: Speciális matematika tantervű gimnáziumok
 

1. Bizonyítsa be, hogy van olyan szám, amely a tízes számrendszerben 987654321-re végződik és osztható 2003-mal!
 
2. Adott egy 10×10×10-es kockarács. Három ember (A, B és C) a következő játékot játssza. Felváltva (A,B,C,A,B,C,...) elhelyeznek a kockarácsban egy-egy 1×1×10-es rudat, három egymásra merőleges irányból. (Mindegyikőjük csak a hozzá tartozó irányból helyezheti el a rúdját.) A rudakat teljesen be kell tolni, nem ütközhetnek egymással, legfeljebb érintkezhetnek. Hány (teljes) körből állhat a leghosszabb játék?
 
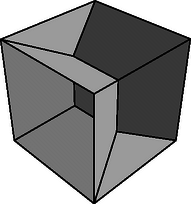
3. A tapasztalat azt mutatja, hogy ha egy drótból készült kockát szappanos vízbe mártunk, egy, az alábbi ábrán szemléltetett szappanhártya alakzat keletkezik, mely egy négyzetből, négy egybevágó egyenlő szárú háromszögből és nyolc egybevágó szimmetrikus trapézból áll. Mutassa meg, hogy az így létrejött hártya felszíne ‐ minden hártyaidomnak csak az egyik oldalát számítva ‐ legfeljebb a tömörnek képzelt kocka felszínének 1112-e. Javítható-e ez a becslés?
 

 
HALADÓK
 

II. kategória: Általános matematika tantervű gimnáziumok
 

Első (iskolai) forduló
 

1. Melyek azok a racionális számokból álló (x;y) számpárok, amelyekre igaz, hogy (x+1y)⋅(y+1x) értéke nullától különböző egész szám?
 
2. Az ABC háromszög BC oldalának C-hez közelebbi harmadolópontja H, AC oldalának C-hez közelebbi negyedelőpontja pedig N. Az AH és BN szakasz a P pontban metszi egymást. Mekkora a PHCN négyszög és az ABP háromszög területének aránya?
 
3. Négy számról, a-ról, b-ről, c-ről és d-ről tudjuk, hogy a belőlük képezhető hat darab kéttagú összeg közül három racionális, három pedig irracionális értékű.
A) Racionális szám-e az a+b+c+d összeg?
B) Hány racionális szám lehet a négy szám között?
 
4. Az ABCD trapéz AD szára merőleges az AB és CD alapra. A BC átmérőjű k kör az AD oldalt az E pontban érinti. Igazoljuk, hogy BE+CE≤2(AB+CD).
 
5. Mely pozitív egész n értékekre igaz, hogy 2n+65 értéke négyzetszám?
 
Második forduló

 
1. Melyik az a háromjegyű szám, amelyre igaz, hogy az első számjegyét letörölve, majd ezt a számjegyet a megmaradó két számjegy után írva olyan háromjegyű számot kapunk, melynek négyzetgyöke 9-cel kisebb az eredeti szám négyzetgyökénél.
 
2. Bármely derékszögű háromszögbe két olyan négyzet írható, amelynek csúcsai a háromszög kerületén vannak. Legfeljebb mekkora lehet a nagyobb és a kisebb négyzet területének aránya?
 
3. Legyen g(x) egész együtthatós polinom.
Bizonyítsuk be, hogy az alábbi polinomnak nincs egész gyöke:
6(x2+1)2+5g(x)⋅(x2+1)-21⋅g2(x).

 
4. Egy 2n-szög mindegyik csúcsára a -1 vagy 1 számot írtuk rá.
Egy lépésben bármelyik (n+1) darab csúcsra írt szám mindegyikének megváltoztathatjuk az előjelét.
Milyen n érték esetén, mely kezdőhelyzetből indulva érhető el a megengedett lépés tetszőleges számú alkalmazásával, hogy mindegyik csúcshoz az 1-es szám tartozzon?
 
Harmadik (döntő) forduló
 

1. Határozzuk meg azokat az x1,x2,...,xn pozitív számokat, amelyekre teljesülnek az
x1+x2+...+xn=3,1x1+1x2+...+1xn=3
összefüggések.
 
2. Az ABC háromszög tetszőleges belső pontjából merőlegeseket állítunk az oldalakra. A kapott három talppont által meghatározott háromszög köréírt köre az eredeti háromszög oldalait újabb három pontban metszi: az AB oldalt P-ben, a BC oldalt Q-ban, az AC oldalt R-ben.
Bizonyítsuk be, hogy a P-n átmenő AB-re merőleges egyenes, a Q-n átmenő BC-re merőleges egyenes és az R ponton átmenő AC-re merőleges egyenes közös pontban metszi egymást.
 
3. Egy síkbeli terepen hat város között három egyenes út vezet. Az első A1-ből B1-be, a második A2-ből B2-be, a harmadik pedig A3-ból B3-ba. Ai-ből (i=1,2,3) egyszerre indul el az fi futár (i=1,2,3) a Bi városba (i=1,2,3), ahol mindegyik futár állandó sebességgel halad.
A közös indulás után a óra elteltével f1 és f2 találkozik, majd ezután b óra elteltével f1 és f3 találkozik, ismét a óra elteltével f2 és f3 halad el egymás mellett, végül újabb b óra elteltével mindhárman egyszerre érnek célba.
Milyen messze lehet B1 B3-tól, ha a>0, b>0 és A1A2=1 km?
 
III. kategória: Speciális matematika tantervű gimnáziumok
 

Első (iskolai) forduló
 

1. Határozzuk meg azokat a p, q, r és n számokat, amelyekre pn+q2=r2 teljesül, ahol p, q, r pozitív prímszám, n pedig pozitív egész szám.
 
2. Az ABC egyenlő szárú derékszögű háromszög AB átfogója 2 egység hosszú. Az átfogó mely P pontjára igaz, hogy a
a) 3PA+6PB+5PC összeg értéke minimális?
b) 3PA+6PB+5PC összeg értéke maximális?
 
3. Az ABCD húrnégyszögben AB<AD.
Forgassuk el a húrnégyszöget az A csúcs körül úgy, hogy a kapott AB'C'D' négyszög B'C' oldalegyenesére illeszkedjen az eredeti négyszög C csúcsa.
Bizonyítsuk be, hogy ekkor a B'D' átló egyenese átmegy a D csúcson!
 
4. Egy táblára felírtuk a pozitív egész számokat növekvő sorrendben 1-től 3n-ig. Jancsi a számok közül ezután n darabot letöröl (saját belátása szerint). Majd Juliska jön, és a megmaradt számok közül aláhúz n darabot. Bizonyítsuk be, hogy Juliska mindig el tudja érni azt, hogy az aláhúzott számok balról jobbra olvasva olyan sorozatot adjanak, amely páratlan számmal kezdődik és felváltva páros, ill. páratlan elemei vannak.
 
Második (döntő) forduló
 

1. A 2003-ad fokú f(x)=a2003x2003+a2002x2002+...+a1x+a0 polinomhoz található olyan pozitív egész p, q és r, amelyekre p<q<r és f(p)=q, f(q)=r és f(r)=p.
Bizonyítsuk be, hogy f(x) összes együtthatója nem lehet egész szám.
 
2. Az ABCDE ötszögbe az oldalakat érintő kör írható. A B, C, D, E csúcsnál lévő szögek egyenlők. Az ötszög beírt köre a P pontban érinti az AE oldalt. Bizonyítsuk be, hogy az AD, PC és EB egyenesek egy ponton mennek át.
 
3. Egy országban, sík terepen hat város között három egyenes út vezet. Az első A1-ből B1-be, a második A2-ből B2-be, a harmadik pedig A3-ból B3-ba.
Ai-ből minden reggel 8 órakor elindul egy fi futár, aki állandó sebességgel haladva pontosan délben érkezik Bi-be (i=1,2,3).
Az út során f1 és f2 9 órakor találkozik, f1 és f3 10 órakor, f2 és f3 pedig 11 órakor.
Milyen hosszú a B1B3 távolság, ha A1 és A2 1 km-re, A2 és A3 pedig 3 km-re fekszik egymástól?