Kezdőlap


Cím:	A 44. Nemzetközi Matematikai Diákolimpia feladatainak megoldásai
Szerző(k):	Csóka Endre , Kiss Demeter , Kocsis Albert Tihamér , Nagy Zoltán Lóránt , Pach Péter Pál , Rácz Béla András
Füzet:	2003/október, 392 - 399. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A hagyományoknak megfelelően ebben az évben is közöljük a nyári matematikai diákolimpia feladatainak a megoldásait úgy, ahogyan a legilletékesebbek, a magyar csapat tagjai leírták. Közreműködésüket köszönjük és ezúton is gratulálunk eredményeikhez.

A szerkesztőség

1. Legyen

A

S = {1,2, ...,1 000 000}

halmaz egy

101

elemű részhalmaza. Bizonyítsuk be, hogy találhatók olyan

t_{1}, t_{2}, ..., t_{100}

számok az

S

halmazban, amelyekre az

\begin{matrix} A_{j} = {x + t_{j} ∣ x \in A} (j = 1,2, ...,100) \end{matrix}

halmazok páronként diszjunktak.

Nagy Zoltán Lóránt megoldása. Legyenek az

A

halmaz elemei

x_{1}, x_{2}, ..., x_{101}

. Az

S

-beli

t_{1}, t_{2}, ..., t_{100}

számok pontosan akkor megfelelők, ha akkor és csak akkor teljesül az

\begin{matrix} x_{j} + t_{p} = x_{k} + t_{q} \end{matrix}

(*)

egyenlőség, ha

p = q

és

j = k

(

1 \leq j, k \leq 101

, és

1 \leq p, q \leq 100

).
Teljes indukcióval megadunk egy megfelelő

t_{n}

sorozatot. Válasszuk

t_{1}

-et tetszőlegesen

S

-ből. Legyen

1 \leq n \leq 100

és tegyük fel, hogy az

S

-beli

t_{1}, t_{2}, ..., t_{n - 1}

számokat már megadtuk a

(*)

feltétel szerint. Megmutatjuk, hogy

t_{n}

is kiválasztható.

t_{n} \in S

pontosan akkor megfelelő, ha

a)

t_{n} \neq t_{i}

(

1 \leq i < n

b)

t_{n} \neq x_{j} - x_{k} + t_{m}

(

j \neq k

1 \leq m < n

).
Az

a)

feltétel a lehetséges értékek közül

(n - 1)

-et, a

b)

pedig legfeljebb

101 \cdot 100 \cdot (n - 1)

-et zár ki. Ez összesen legfeljebb

\begin{matrix} (n - 1) (101 \cdot 100 + 1) \leq 99 (101 \cdot 100 + 1) = (100 - 1) (100^{2} + 100 + 1) = 100^{3} - 1. \end{matrix}

Mivel

S

-nek

100^{3}

eleme van, azért marad nem kizárt érték

t_{n}

számára, a bizonyítást befejeztük.

2. Határozzuk meg az összes olyan, pozitív egészekből álló

(a, b)

párt, amire

\begin{matrix} \frac{a^{2}}{2 a b^{2} - b^{3} + 1} \end{matrix}

pozitív egész.

Pach Péter Pál megoldása. Azokat az

(a; b)

pozitív egész számpárokat kell megkeresnünk, amelyekre

n = \frac{a^{2}}{2 a b^{2} - b^{3} + 1}

szintén pozitív egész szám.
Vizsgáljuk meg először a

b = 1

esetet. Ekkor a nevező

2 a

, a tört értéke

\frac{a^{2}}{2 a} = \frac{a}{2}

. Ez pontosan akkor egész, ha

a

páros. Így tetszőleges

j

pozitív egészre

(2 j; 1)

megoldás és minden más esetben

b > 1

.
Az

n = \frac{a^{2}}{2 a b^{2} - b^{3} + 1}

egyenlőségből beszorzás és rendezés után egy

a

-ban másodfokú egyenletet kapunk:

a^{2} - 2 n b^{2} a + n b^{3} - n = 0

. Ha fennáll az eredeti egyenlőség, akkor ennek is teljesülnie kell. A másodfokú egyenlet megoldóképletéből

a

-ra kapjuk, hogy

a = n b^{2} \pm \sqrt[]{n^{2} b^{4} - n b^{3} + n}

. Mivel

a

b

n

pozitív egészek, az egyenlet diszkriminánsának,

(n^{2} b^{4} - n b^{3} + n)

-nek négyzetszámnak kell lennie. Megmutatjuk, hogy a diszkrimináns egy bizonyos értelemben ,,szomszédos'' számok közé szorítható, pontosabban

\begin{matrix} {(n b^{2} - \frac{b + 1}{2})}^{2} < n^{2} b^{4} - n b^{3} + n < {(n b^{2} - \frac{b - 1}{2})}^{2} . \end{matrix}

(1)

A négyzetre emeléseket elvégezve rendezés után azt kell igazolnunk, hogy

\begin{matrix} - n b^{2} + {(\frac{b + 1}{2})}^{2} < n < n b^{2} + {(\frac{b - 1}{2})}^{2} . \end{matrix}

A felső becslés nyilvánvaló, hiszen

n \geq 1

és

b > 1

miatt

{(\frac{b - 1}{2})}^{2} > 0

. Az alsó becslést rendezzük át:

\begin{matrix} {(\frac{b + 1}{2})}^{2} < n (b^{2} + 1) . \end{matrix}

Mivel

1 < b

, azért

{(\frac{b + 1}{2})}^{2} < {(\frac{b + b}{2})}^{2} = b^{2}

, ami

n \geq 1

miatt kisebb, mint a jobb oldal. Ezzel az (1) egyenlőtlenségeket igazoltuk.
Látható, hogy ha

b

páratlan, akkor (1)-ben a diszkrimináns két szomszédos egész szám négyzete közé esik, tehát nem lehet négyzetszám. Így

b

szükségképpen páros szám, legyen

b = 2 k

.
Vegyük észre, hogy (1)-ből nyilvánvalóan következnek az alábbi, gyengébb becslések is:

\begin{matrix} {(n b^{2} - (\frac{b}{2} + 1))}^{2} < n^{2} b^{4} - n b^{3} + n < {(n b^{2} - (\frac{b}{2} - 1))}^{2} . \end{matrix}

(2)

[(1) bal oldalát csökkentettük, a jobb oldalát pedig növeltük.]
Ha

b

páros, akkor a (2)-ben kapott korlátok másodszomszédos négyzetszámok, közéjük egyetlen négyzetszám esik, így ebben az esetben a diszkrimináns,

n^{2} b^{4} - n b^{3} + n = {(n b^{2} - \frac{b}{2})}^{2}

.
Innen azt kapjuk, hogy

n = {(\frac{b}{2})}^{2} = k^{2}

és a diszkrimináns,

D = {(4 k^{4} - k)}^{2}

. Ekkor

a = n b^{2} \pm \sqrt[]{D} = 4 k^{4} \pm (4 k^{4} - k)

, azaz vagy

a = 8 k^{4} - k

, vagy pedig

a = k

.
A feladat megoldásai tehát a

(2 k; 1)

(8 k^{4} - k; 2 k)

(k; 2 k)

alakú számpárok, ahol

k

pozitív egész.
Az utóbbi két számpárt ellenőrizve kapjuk, hogy megoldásai a feladatnak.

3. Adott egy konvex hatszög, amelyben bármely két szemközti oldalra teljesül a következő tulajdonság: az oldalak középpontjai közötti távolság

\frac{\sqrt[]{3}}{2}

-szerese a hosszuk összegének. Bizonyítsuk be, hogy a hatszög valamennyi szöge egyenlő.
(Az

A B C D E F

konvex hatszögben három szemközti oldalpár van:

A B

és

D E

B C

és

E F

C D

és

F A

Csóka Endre megoldása. Először igazoljuk az alábbi segédtételt: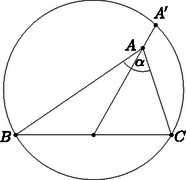

Legyen egy

A B C

háromszög

A

csúcsánál

α

szög, az

A

-ból induló súlyvonal

s

, az

A

-val szemközti oldal pedig

a

. Ha

α \geq 60^{\circ}

, akkor

s \leq \frac{\sqrt[]{3}}{2} a

és egyenlőség csak szabályos háromszögre teljesül.

Bizonyítás. Föltehető, hogy

α = 60^{\circ}

, egyébként ugyanis az

A

-ból induló súlyvonalat az

A

-n túl meghosszabbíthatjuk addig a látókörig, amelynek pontjaiból a

B C

szakasz

60^{\circ}

-os szögben látszik (1. ábra). Az

A'

-ből induló súlyvonal így nő, az

A'

-vel szemközti oldal hossza továbbra is

a

1. ábra

Legyen tehát

α = 60^{\circ}

, a

B C

oldal felezőpontja

F

, a körülírt kör nagyobbik

B C

ívének felezőpontja pedig

A_{1}

(2. ábra). Ekkor

A_{1} F = \frac{\sqrt[]{3}}{2} a

és

A F = s

, így azt kell igazolnunk, hogy

A F \leq A_{1} F

és pontosan akkor van egyenlőség, ha

A = A_{1}

, az

A B C

háromszög szabályos.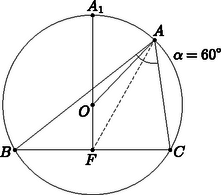

2. ábra

Jelölje

O

a kör középpontját. Ekkor a háromszög egyenlőtlenség szerint

A F \leq A O + O F = A_{1} O + O F = A_{1} F

és valóban akkor van egyenlőség, ha

A_{1} O

és

F

egy egyenesre esnek, azaz

A = A_{1}

. Ezzel a segédtételt igazoltuk.

\begin{matrix}  \end{matrix}

Legyenek a hatszög csúcsai pozitív körüljárás szerint betűzve (3. ábra) és tetszőleges

P Q

szakasz felezőpontját jelölje

F_{P Q}

. Tegyük fel, hogy az

A D

és

B E

átlók

M_{1}

metszéspontjára a pozitív

A M_{1} B \geq 60^{\circ}

. A segédtétel szerint

\sqrt[]{3}

2(AB+DE)≥FABM1+M1FDE,