Kezdőlap


Cím:	A matematika és fizika totó eredménye (2002.évi Téli Ankét)
Füzet:	2003/március, 166. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A múlt havi számunkban közreadtuk a 2002. évi Téli Ankét totó-kérdéseit. A telitalálatos szelvény:

\begin{matrix} 1,2,2,  2,2,1,  2,X,1,  X,2,2,  1,2. \end{matrix}

Telitalálatos szelvény nem volt. 13 találatot ért el és könyvjutalmat kapott Egri Attila (Hajdúszoboszló, Hőgyes E. Gimn., 11. évf.), Pallos Péter (BME hallgató) és Simon Balázs (Győr, Révai M. Gimn., 12. évf.). Az alábbiakban rövid útmutatást adunk a feladatok megoldásához.

1. A kombinatorikát (amelybe beletartozott a véges csoportok elmélete is) hívták a tizenkilencedik században ,,kapcsolástannak''.

2. A közegellenállási erő a megadott végsebességnél (10 m/s-nál) éppen megegyezik a nehézségi erővel, fele ekkora vagy még annál is kisebb sebességnél legfeljebb a gravitációs erő negyedrészét éri el. Első közelítésben elhanyagolva a légellenállást a kérdéses útra

\begin{matrix} s = \frac{v^{2}}{2 g} = 1, 25 m \end{matrix}

adódik, a pontosabb eredmény ennél kicsit (kb. 10‐20%-kal) nagyobb lehet.

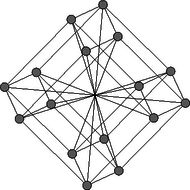
3. A társaság lehet négytagú (a gráfja egy ,,négyzet''). Lehetnek azonban 4-nél többen is, erre mutat példát az ábra.

4. A tükörképek a fényforrás és a tükrök (geometriai értelemben vett) sorozatos tükrözésével kaphatók meg, ezek közül azonban a tükrök véges mérete és a takarások miatt mindig csak véges sok látható.

5. A

t

-vel jelölt számjegyet nélkülöző

n

-jegyű számok legkisebbike legalább

10^{n - 1}

, az ilyen számok száma pedig legfeljebb

9^{n}

. Ezért reciprokuk összege kisebb, mint

\begin{matrix} \sum_{n \geq 1}^{} \frac{9^{n}}{10^{n - 1}} = 9 \cdot \frac{1}{1 - \frac{9}{10}} = 90. \end{matrix}

6. Az

ω

szögsebességgel forgó,

Θ

tehetetlenségi nyomatékú test perdülete

N = Θ ω

, forgási energiája pedig

\begin{matrix} E_{f} = \frac{1}{2} Θ ω^{2} = \frac{N^{2}}{2 Θ} . \end{matrix}

A jégtáncos ‐ miközben behúzza karjait ‐ a tehetetlenségi nyomatékát lecsökkenti, perdülete közel állandó marad, a forgási energiája tehát növekszik. (Az ehhez szükséges munkát a kar- és vállizmai végzik.)

7. Egyetlen olyan megoldás van, ahol

a = b = c

, ez

2 \cdot 3 a = 3 a^{2}

-ből

a = 2

. Ha pl.

a = b \neq c

, akkor

\begin{matrix} 4 a + 2 c = a^{2} + 2 a c \end{matrix}

szerint

a

páros, akkor viszont a jobb oldal 4-gyel osztható, tehát

c

is páros:

a = 2 x

c = 2 y

. Így

\begin{matrix} 2 x + y = x^{2} + 2 x y . \end{matrix}

Itt a jobb oldal csak akkor nem nagyobb a bal oldalnál, ha

x = 1

, de akkor

y = 1

, ami ellentmondás. Végül, ha pl.

a < b < c

, akkor

\begin{matrix} 2 c < (a + b) c, így 2 (a + b) > a b, \end{matrix}

azaz

(a - 2) (b - 2) \leq 3

, ezért

a \leq 3

. Ha

a = 1

, akkor

(b - 1) (c - 1) = 2

, ezért

b = 2

és

c = 3

. Az

a

b

és

c

permutációit figyelembe véve ez 6 megoldást ad. Ha

a = 2

, akkor

b c = 4

, ami lehetetlen. Ha pedig

a = 3

, akkor

(b + 1) (c + 1) = 7

, ami ugyancsak lehetetlen. Összesen tehát

1 + 6 = 7

megoldás adódott.

8. Általános termodinamikai összefüggéseket kihasználva belátható, hogy a (fajhőkkel arányos) hőkapacitásokra fennáll

\begin{matrix} C_{p} - C_{v} = \frac{T V α^{2}}{κ_{T}}, \end{matrix}

ahol

α

az izobár hőtágulási együttható (ennek négyzete szerepel a képletben, tehát az előjele érdektelen),

κ_{T}

pedig az izoterm kompresszibilitás, ami ugyancsak pozitív. Emiatt az állandó nyomáson mért fajhő (hőkapacitás) minden anyagra, még a negatív hőtágulási együtthatóval leírhatókra is nagyobb, mint az állandó térfogaton mért fajhő (hőkapacitás).

9. Az 1-essel összesen 24 szám kezdődik, ez összesen

5 \cdot 24 = 120

számjegy. Ugyanennyi 2-essel és 3-assal kezdődő szám van, ami az elöbbiekkel együtt

3 \cdot 120 = 360

számjegy. A 41-gyel kezdődő számok és a 42-vel kezdődőek is hatan vannak, ez további

12 \cdot 5 = 60

számjegy, az eddigiekkel összesen

360 + 60 = 420

, maradt még

433 - 420 = 13

. Az első három

43

-mal kezdődő szám: 43125, 43152, 43215, közülük a 13-adik számjegy a 2-es.

10. A Balmer-formula segítségével belátható, hogy a különböző energiaszint-pároknak megfelelő fotonok között nincs ugyanakkora frekvenciájú. A 7. energiaszintről alapállapotba ,,egyesével'' ugrálva 6 különböző hullámhosszúságú foton keletkezhet, egy szintet átugorva 5 különböző foton sugárzódhat ki és így tovább, a különböző fotonok száma tehát

\begin{matrix} 6 + 5 + 4 + 3 + 2 + 1 = 21. \end{matrix}

11. A három ajtó közül kettő mögött kecske van. Ha a játékos először ezek valamelyikére mutatott, akkor ‐ mivel a játékvezető felfedte a másik kecske helyét ‐ változtatás esetén nyer. Ha viszont kezdetben arra az egy ajtóra mutatott, amelyik mögött az autó van, akkor változtatás esetén veszít.
Annak a valószínűsége, hogy először olyan ajtóra mutat a játékos, ami mögött kecske van,

2 / 3

. Tehát ha az eredeti döntését mindig megváltoztatja, akkor

2 / 3

eséllyel nyer.

12. A Föld felszínének közelében kb.

E = 130

V/m erősségű elektromos tér figyelhető meg, ennek energiasűrűsége

\begin{matrix} w_{e} = \frac{1}{2} ε_{0} E^{2} \approx 10^{- 7} \frac{J}{m^{3}} . \end{matrix}

A földmágnességből származó mágneses indukció pl. Budapesten (átlagosan)

B = 2 \cdot 10^{- 5} T

nagyságú, az ennek megfelelő mágneses energiasűrűség pedig

\begin{matrix} w_{m} = \frac{1}{2 μ_{0}} B^{2} \approx 10^{- 4} \frac{J}{m^{3}} . \end{matrix}

Egy bizonyos térfogatra jutó mágneses energia tehát mintegy 1000-szer nagyobb, mint az ugyanakkora térfogathoz tartozó elektromos energia. Ennek a meglepően nagy aránytalanságnak a magyarázatát a légköri elektromosság és a földmágnesség különböző eredetében kereshetjük. Az elektromos mezőt a zivatarfelhőkben végbemenő töltésszétválás és a felszálló légmozgás hozza létre, a földmágnesség forrása pedig a Föld megolvadt magjában kialakuló konvektív plazmaáramlás. Mindkét jelenségkör nagyon összetett, bonyolult, és még nem minden részletében megértett folyamat.

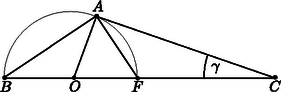
13. Jelöljük a

B C

oldal felezőpontját

F

-fel. Az

A

pont a

B F

szakasz fölé emelt Thalész-körön helyezkedik el, és a legkisebb szög (a

C

csúcsnál levő

γ

) akkor a legnagyobb, ha

C A

érinti a Thalész-kört. Ekkor

\begin{matrix} sin γ = \frac{O A}{O C} = \frac{1}{3}, azaz γ \approx 19, 47^{\circ} . \end{matrix}

13+1. Mivel nem akarjuk pontosan meghatározni az ütközések várható számát, hanem csak nagyságrendi becslést szeretnénk adni, az egyszerűség kedvéért tekintsük úgy, mintha minden ember mozdulatlan volna, csupán egyetlen kiszemelt ember mozogna egy találomra kiválasztott másik felé. A két kiválasztott ember távolságát becsülhetjük a pl. futballpálya átlójának felével, kb. 60 m-rel. Az ütközések száma a ,,nyílegyenes'' vonal jobb és bal oldali fél-fél méteres oldalsávjában, tehát összesen 60 m

^{2}

-nyi területen tartózkodó emberek átlagos számával egyenlő, ez pedig a

\begin{matrix} \frac{10 000 ember}{70 m \cdot 100 m} = 1, 4 \frac{ember}{m^{2}} \end{matrix}

átlagsűrűségből számíthatóan kb. 80. (A feladat a gáz- és folyadékmolekulák ütközését modellezi.)