Cím: 2002. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása
Szerző(k):  Károlyi Gyula 
Füzet: 2003/február, 67 - 77. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd), Matematika, Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Egy hegyesszögű háromszög oldalai páronként különbözők; magasságpontja M, beírt körének középpontja K, körülírt körének középpontja pedig O. Bizonyítsuk be, hogy ha egy kör átmegy a K, O, M pontokon és a háromszög egyik csúcsán, akkor átmegy egy másik csúcson is.

 
I. megoldás. A K, O, M pontok a háromszög belsejében helyezkednek el. Ha a csúcsokat A, B, C, a megfelelő szögeket α, β, γ jelöli, akkor BAM∢=90∘-β=CAO∢. Itt a második egyenlőség abból következik, hogy az AOC egyenlő szárú háromszögben a kerületi és középponti szögek tétele miatt AOC∢=2β. Mivel az AK félegyenes felezi a BAC szöget, megállapíthatjuk, hogy az AM és AO félegyenesek az AK félegyenesre szimmetrikusan helyezkednek el. A három félegyenes nem eshet egybe (különben a háromszög egyenlő szárú lenne). Azt kaptuk tehát, hogy a KM és KO szakaszok az A csúcsból ugyanolyan szög alatt látszanak, továbbá az AK egyenes elválasztja az M és O pontokat. Ez az állítás természetesen akkor is igaz, ha A helyébe a háromszög B vagy C csúcsát írjuk.
Tegyük fel most, hogy az A, M, K, O pontok egy körön helyezkednek el. A kerületi szögek tételének megfordítása szerint a KM és KO szakaszok hossza ekkor egyenlő. Ez a két szakasz a háromszög csúcsaiból ugyanolyan szög alatt látszik. Vizsgáljuk meg tehát, hogy mi azon P pontok mértani helye, melyekből a két egyenlő szakasz ugyanolyan szög alatt látszik.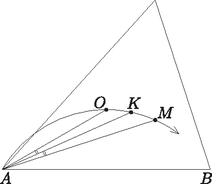
 
 

1. ábra
 

Ha egy adott P-re ez a szög φ, akkor P illeszkedik valamelyik, a KM szakaszra emelt φ szöghöz tartozó i látókörívre, és ugyanígy valamelyik, a KO szakaszra emelt φ szögű j látókörívre is. Azt mondjuk, hogy az i ívet a KM szakaszra befelé emeltük, ha az i ív és az O pont a KM egyenesnek ugyanazon az oldalán helyezkednek el; ellenkező esetben kifelé emelt látókörívről beszélünk. Félreértésről itt nem lehet szó, hiszen a feltétel szerint a K, O és M pontok nem esnek egy egyenesre. Ezt a szóhasználatot értelemszerűen követjük a j ívre vonatkozóan is.
Ha az i és j ívet is kifelé emeltük, akkor metszéspontjuk, amennyiben létezik, az MO szakasz f felező merőlegesén helyezkedik el, hiszen KM=KO miatt a két kör egybevágó. Ugyanez a helyzet akkor is, ha mindkét ívet befelé emeltük. Az egyetlen kivétel, ha a két látókörívnek közös K végpontjukon kívül még legalább két közös pontja van. Ez pontosan akkor következik be, ha a két ív ugyanannak a körvonalnak, vagyis a K, O, M pontokra illeszkedő k körvonalnak a része.
Elképzelhető-e, hogy valamelyik ívet (mondjuk az i ívet) kifelé, míg a másik ívet befelé emeltük? A két ív ebben az esetben pontosan akkor metszi egymást, ha φ kisebb a KMO szögnél. Ekkor j metszi az OM szakasz M-en túli meghosszabbítását, ahonnan a KM és KO szakaszok ugyanolyan szög alatt látszanak, vagyis éppen ez a pont lesz a két körív metszéspontja. Egy ilyen pont azonban nem lehet az ABC háromszög csúcsa, mert ekkor az ezen a csúcson és K-n átmenő egyenes nem választaná el az M és O pontok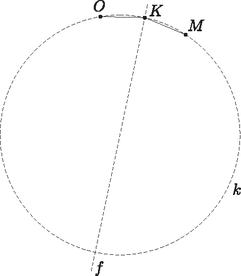at.
 
 

2. ábra
 

Összefoglalva megállapíthatjuk, hogy a háromszög minden egyes csúcsa vagy az f egyenesen, vagy a k körvonalon helyezkedik el. Mivel a K pont illeszkedik f-re, a csúcsok közül legfeljebb egy eshet f-re, vagyis legalább kettő a k körvonalra esik, és éppen ezt kellett bizonyítanunk.
 
II. megoldás (Rácz Béla András megoldása alapján). Jelölje a háromszög csúcsait A, B, C, és tegyük fel, hogy az A, M, K, O pontok egy k körön helyezkednek el. Jegyezzük meg, hogy ez a k kör egyértelmű, hiszen a négy pont különböző. Ahogyan azt az előző megoldás során láttuk, KM=KO, vagyis K illeszkedik az MO szakasz f felező merőlegesére. Jegyezzük meg, hogy a B, O és M pontok nem esnek egy egyenesre, mert abban az esetben AB=BC lenne.
Tekintsük az MBO szög e szögfelezőjének az MBO háromszög köré írt ℓ körrel alkotott L metszéspontját. A kerületi szögek tételének megfordítása miatt ML=LO, vagyis az L pont illeszkedik az f egyenesre. Amint az előző megoldás első felében kiderült, a K pont is illeszkedik az e egyenesre és az f egyenesre, most pedig látszik, hogy ugyanez az L pontra is igaz. Következésképpen, ha az e és f egyenesek nem esnek egybe, akkor K=L, vagyis a B, O, K és M pontok egyaránt az ℓ körre illeszkednek. Mivel a K, O, M pontok különbözők, szükségképpen k=ℓ, vagyis k átmegy a háromszög B csúcsán is.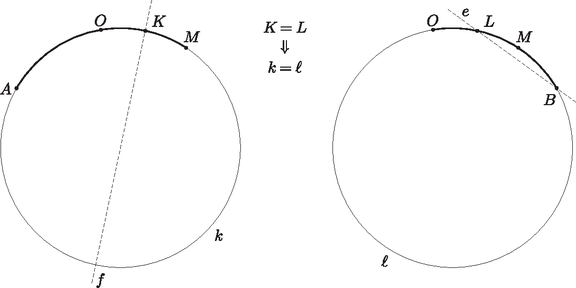
 
 

3. ábra
 

Ha az e és f egyenes egybeesik, akkor f áthalad a B csúcson, vagyis BM=BO=R, ahol R az ABC háromszög köré írt kör sugara. Ha azonban MC az M pontnak az AB oldalra eső merőleges vetülete, akkor 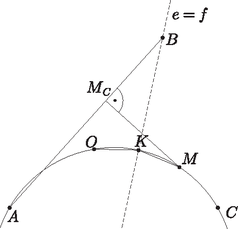BMC=BCcosβ=2Rsinαcosβ, vagyis
BM=BMCsinα=2Rcosβ.
Ezért cosβ=12, β=60∘. Egyszerű szögszámolással adódik, hogy ekkor az AC szakasz az M, K és O pontok mindegyikéből 120∘ szög alatt látszik. Mivel az M, K, O pontok az AC egyenesnek ugyanazon az oldalán vannak, ilyenkor az A, M, K, O, C pontok vannak egy körön, amely nem lehet más, mint k.
 
 

4. ábra

 
III. megoldás (Harangi Viktor megoldása alapján). Ahogyan azt már korábban is láttuk, a K, O, M pontok különbözők, KM=KO és az OM egyenes nem halad át az ABC háromszög egyetlen csúcsán sem. Tegyük fel, hogy az OM egyenes elválasztja az A csúcsot a többi kettőtől. Ekkor az OM szakasz f felező merőlegese (amely illeszkedik a K pontra) szükségképpen metszi a BC oldalt. Ellenkező esetben ugyanis az M és O pontok közül valamelyik (mondjuk M) a B és C pontokhoz is a másiknál közelebb helyezkedne el. Mivel K egyaránt rajta van az MBO és MCO szögek szögfelezőjén, a szögfelező tétel miatt a BK és a CK egyenes is M-hez közelebb metszené az OM szakaszt, ami miatt K is közelebb helyezkedne el M-hez, mint O, ami ellentmondásra vezetne.
A B és C csúcsok közül tehát az egyik az f egyenesnek ugyanazon az oldalán van, mint M, a másik pedig O-val van megegyező oldalon. Az általánosság megszorítása nélkül feltehetjük, hogy BM≤BO és CM≥CO, ahol legalább az egyik helyen határozott egyenlőtlenség áll. Az MO szakaszt tehát a BK egyenes M-hez, a CK egyenes pedig O-hoz metszi közelebb (valamelyik metszéspont esetleg egybeeshet az MO szakasz felezőpontjával, mindkettő azonban nem). Következésképpen az OM egyenes elválasztja a K pontot a B és C csúcsoktól. Megállapíthatjuk tehát, hogy a B és C csúcs is az MKO szögtartományban helyezkedik el.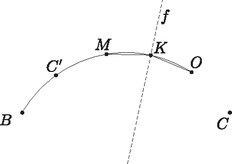
 
 

5. ábra
 

Tükrözzük most a C pontot az f egyenesre, így kapjuk a C' pontot. Ekkor KC'O∢=KCM∢=KCO∢ miatt, és mert C, C' a KO egyenes ugyanazon oldalára esik, láthatjuk, hogy a K, C, C', O pontok egy körön helyezkednek el, ami szimmetria okok miatt az M ponton is átmegy. C tehát illeszkedik a KOM háromszög köré írt körre. Ugyanilyen okok miatt B is illeszkedik erre a körre, az A csúcs viszont nem, hiszen az MO egyenes nem választja el az A és K pontokat. Ezzel az állítást bebizonyítottuk.
 

Megjegyzések. Szükség van-e arra a feltételre, hogy a háromszög oldalai páronként különbözők? Ha a háromszög egyenlő szárú, akkor a K, O, M pontok egy egyenesre esnek. Egy kör tehát csak akkor mehet át mindhárom ponton, ha közülük kettő egybeesik, vagyis ha a háromszög szabályos. Elegendő lett volna tehát annyit feltenni, hogy egy szabályostól különböző hegyesszögű háromszögről van szó.
Ha a háromszög nem hegyesszögű, akkor persze szabályos sem lehet, tehát nincsen szükség ilyen feltételre. Ha azonban a háromszög derékszögű, akkor az M pont egybeesik a háromszög egyik csúcsával. Ha tehát egy kör átmegy a K, O, M pontokon, akkor szükségképpen átmegy a háromszög egyik csúcsán is. Egy másik csúcson viszont akkor és csak akkor mehet át, ha a harmadik csúcsnál lévő szög 60∘. (Miért?) Derékszögű háromszögekre ezek szerint nem érvényes az állítás. Mi a helyzet, ha valamelyik szög tompaszög? Ebben az esetben valamivel több diszkusszióra van szükségünk a megoldás során, az állítás mindazonáltal érvényben marad.
 
Feladatok
1) Egy tompaszögű háromszög magasságpontja M, beírt körének középpontja K, körülírt körének középpontja pedig O. Bizonyítsuk be, hogy ha egy kör átmegy a K, O, M pontokon és a háromszög egyik csúcsán, akkor átmegy egy másik csúcson is.
2) Egy derékszögűtől különböző háromszöghöz pontosan akkor van olyan kör, amely átmegy a K, O, M pontokon és a háromszög egyik csúcsán, ha a háromszög valamelyik szöge 60∘.
 
2. feladat. Tekintsük a Fibonacci-számok f1=f2=1, fn=fn-1+fn-2 (n≥3) rekurzióval meghatározott sorozatát. Tegyük fel, hogy az a és b pozitív egész számokra az ab tört az fnfn-1 és fn+1fn törtek egyikénél kisebb, másikánál nagyobb. Mutassuk meg, hogy b≥fn+1.
 
I. megoldás (Kocsis Albert Tihamér és Zsbán Ambrus megoldása alapján). Az állítást n-re vonatkozó teljes indukcióval bizonyítjuk. Először is győződjünk meg arról, hogy az állítás n=2,3 esetén igaz. Valóban, ha n=2, akkor feltételünk 1<ab<2, ahonnan b≥2=f3. Ha pedig n=3, akkor 32<ab<2 miatt b≥3=f3. A továbbiakban tegyük fel tehát, hogy m≥3 és az állítást 2≤n≤m esetén már igazoltuk.
Legyen most n=m+1, és tegyük fel, hogy fnfn-1<fn+1fn, továbbá az a, b pozitív egészekre fm+1fm=fnfn-1<ab<fn+1fn=fm+2fm+1. Az egyenlőtlenségben szereplő számokat eggyel csökkentve kapjuk, hogy
fm-1fm=fm+1-fmfm<a-bb<fm+2-fm+1fm+1=fmfm+1.
Mivel az egyenlőtlenség mindkét szélén (és így középen is) pozitív számok állnak, a benne szereplő kifejezések reciprokát véve az egyenlőtlenség iránya megváltozik, és a következőt kapjuk:
fmfm-1>ba-b>fm+1fm.
Ezért az indukciós feltevésünk alapján a-b≥fm+1. Az imént nyert egyenlőtlenségben szereplő számokat megint eggyel csökkentve, majd az így kapott számok reciprokát véve most az
fm-1fm-2<a-b2b-a<fmfm-1
egyenlőtlenségre jutunk, ahonnan ismét az indukciós feltételt alkalmazva megállapíthatjuk, hogy 2b-a≥fm.
Az így nyert két eredményt összegezve:
b=(2b-a)+(a-b)≥fm+fm+1=fm+2=fn+1
adódik, ami azt jelenti, hogy ebben az esetben az állítás n=m+1 esetén is igaz. Hogy az indukciós lépést teljessé tegyük, meg kell vizsgálnunk azt is, mi történik, ha fm+1fm=fnfn-1>ab>fn+1fn=fm+2fm+1. Ebben az esetben is szóról szóra elmondhatjuk az előző érvelést; az egyetlen különbség, hogy a felírt egyenlőtlenségekben mindenhol fel kell cserélnünk a ,,<'' és ,,>'' relációk szerepét.
 
II. megoldás (Egri Attila megoldása alapján). A megoldás során feltesszük, hogy fnfn-1<ab<fn+1fn. Minden számot megszorozva a pozitív bfn-1fn számmal a
bfn2<afn-1fn<bfn-1fn+1
egyenlőtlenségre jutunk. Itt az első két szám különbsége, fn⋅(afn-1-bfn) olyan pozitív egész szám, amely osztható fn-nel, ezért nagysága legalább fn. Hasonló okok miatt a második két szám különbsége, fn-1⋅(bfn+1-afn) legalább fn-1. Következésképpen a két szélső szám különbsége:
b(fn-1fn+1-fn2)≥fn+fn-1=fn+1.
Elegendő tehát annyit megmutatni, hogy kn=fn-1fn+1-fn2=1.
Ha n=2, akkor kn=1, ha pedig n=3, akkor kn=-1. Még néhány értéket megvizsgálva azt tapasztaljuk, hogy kn értéke felváltva 1 és -1, vagyis kn=(-1)n. Valóban, n=2 esetén ez így van, ha pedig valamely n≥2 egész számra már beláttuk, akkor
kn+1=fnfn+2-fn+12=fn(fn+fn+1)-fn+12==fn2-fn+1(fn+1-fn)=fn2-fn+1fn-1=-kn=-(-1)n=(-1)n+1.

Mivel esetünkben b és fn+1 is pozitív, szükségképpen kn is pozitív, vagyis értéke nem lehet más, mint 1, amint azt bizonyítani kívántuk. Teljesen hasonló módon járhatunk el akkor is, ha fnfn-1>ab>fn+1fn.
 

Megjegyzés. Ebből a megoldásból leolvasható az az általánosabb eredmény is, mely szerint ha az a, b, x, y, z, v pozitív egészekre yz-xv=1 és xy<ab<zv, akkor szükségképpen b≥y+v.
 
III. megoldás. Tegyük fel az egyszerűség kedvéért, hogy n páros. Az előző megoldás során használt fn-1fn+1-fn2=(-1)n összefüggés alapján tehát a feltétel most fnfn-1<ab<fn+1fn alakban teljesül. Az
ab-fnfn-1=afn-1-bfnbfn-1
különbség pozitív, ezért itt az egész értékű számláló legalább 1. Következésképp
1bfn-1≤ab-fnfn-1<fn+1fn-fnfn-1=1fn-1fn,
ahonnan bfn-1>fn-1fn, vagyis b>fn.
Vizsgáljuk az fn+2fn+1 törtet, ez kisebb, mint fn+1fn. Ha
fn+2fn+1<ab<fn+1fn
is teljesül, akkor az előző érveléshez hasonló módon kapjuk, hogy
1bfn≤fn+1fn-ab<fn+1fn-fn+2fn+1=1fn+1fn,
ahonnan b>fn+1.
Ha ab=fn+2fn+1, akkor b≥fn+1, ugyanis fn+2 és fn+1 relatív prímek. Erről így győződhetünk meg: ha egy d pozitív egész szám osztója fn+2-nek és fn+1-nek is, akkor osztója az fn=fn+2-fn+1 különbségnek is. Ezt a gondolatmenetet tovább folytatva látható, hogy d osztója az fn-1,fn-2,...,f1 számoknak is. Mivel f1=1, d nem lehet más, mint 1.
Már csak azt kell megvizsgálnunk, mi van akkor, ha fnfn-1<ab<fn+2fn+1. Ehhez az ℓn=fn+2fn-1-fnfn+1 különbséget tekintve, teljes indukcióval könnyen kapható, hogy ℓn=(-1)n, és ezért
1bfn-1≤ab-fnfn-1<fn+2fn+1-fnfn-1=1fn+1fn-1,
ahonnan ismét b>fn+1 adódik.
Teljesen hasonló eljárással érhetünk célt akkor is, ha n páratlan szám.
 

Többen az úgynevezett Farey-sorozatok elméletét használták fel bizonyításuk során. Az alábbiakban erre mutatunk egy példát.
 
IV. megoldás (Pallos Péter megoldása alapján). Az F1=(01;11) sorozatból kiindulva rekurzív módon készítsük el a következő sorozatokat. Ha az Fn sorozatot már definiáltuk, akkor annak bármely két egymást követő ab és cd eleme közé illesszük be az a+cb+d törtet. Könnyű ellenőrizni, hogy ha az Fn sorozat szigorúan növekedő volt, akkor ugyanez igaz az így kapott Fn+1 sorozatra is. Megoldásunk az alábbi két tételre támaszkodik: 1) az Fn sorozatban minden tört redukált alakban jelenik meg; 2) minden 0 és 1 közé eső racionális szám eleme valamelyik Fn sorozatnak.
Vegyük észre, hogy fn-1fn és fnfn+1 szomszédos elemei az Fn sorozatnak. Valóban, ez n=2 esetén így van, ha pedig valamely n≥2 egész számra fn-1fn és fnfn+1 az Fn sorozat szomszédos elemei, akkor az Fn+1 sorozatban e két tört közé éppen az
fn-1+fnfn+fn+1=fn+1fn+2
törtet illesztjük be, így az állítás n+1-re is teljesülni fog.
Mivel az fn sorozat szigorúan növekedő, a feladatban szereplő ab tört 1-nél nagyobb. A fent említett tételek alapján a ba tört tehát valamilyen redukált b'a' alakban megjelenik valamely Fm sorozatban. Mivel b'a' az fn-1fn és fnfn+1 törtek egyikénél nagyobb, másikánál kisebb, nyilvánvaló, hogy m>n. Az Fm sorozatok konstrukciójából adódóan viszont látható, hogy minden, az fn-1fn és fnfn+1 közé bekerülő tört számlálója legalább fn-1+fn lesz, amiért is
b≥b'≥fn-1+fn=fn+1,
ahogyan azt bizonyítani akartuk.
 

Megjegyzés. Ebben a megoldásban tulajdonképpen ,,ágyúval lőttünk verébre'', tudniillik a Farey-sorozatokra vonatkozó tételek bizonyításához éppen azokra a gondolatokra van szükség, amelyeket az előző megoldások során használtunk.
 
3. feladat. Bizonyítsuk be, hogy egy konvex 3n-szög összes oldalából és átlójából álló szakaszrendszert hármas csoportokra lehet osztani úgy, hogy minden egyes csoportban a három szakasz egy háromszög-vonalat alkot.
 
I. megoldás (Csikvári Péter megoldása alapján). A sokszög csúcsaihoz rendeljük hozzá a 0,1,2,...,3n-1 számokat, 3-as számrendszerben felírva. Minden leírt számnak legfeljebb n jegye van. Ha a jegyek száma n-nél kisebb, akkor írjunk a szám elé még annyi 0 számjegyet, hogy végül egy n számjegyből álló sorozatot kapjunk, amelynek tehát minden számjegye 0, 1 vagy 2. Úgy is fogalmazhattunk volna, hogy a sokszög csúcsaihoz rendeljük hozzá az n hosszúságú 0‐1‐2 sorozatokat.
Tekintsük azokat a háromszögeket, melyekre teljesül a következő feltétel: bármelyik helyiértéket választjuk is ki, a háromszög csúcsaihoz rendelt három szám az adott helyiértéken vagy mind megegyezik, vagy páronként különböző. Világos, hogy bármely két csúcsot kiválasztva, pontosan egy olyan csúcsa lesz a sokszögnek, hogy a három csúcs által meghatározott háromszög kielégíti a fenti feltételt. Az eredeti sokszögnek tehát minden egyes oldala és átlója pontosan egy háromszögnek lesz valamelyik oldala, ami azt jelenti, hogy azok a szakasz-hármasok, melyek egy-egy háromszög három oldalát alkotják, rendelkeznek a feladatban megkövetelt tulajdonsággal.
 
II. megoldás. A bizonyítást n-re vonatkozó teljes indukcióval végezzük. Ha n=1, akkor az állítás nyilvánvaló. Az indukciós lépéshez tegyük fel, hogy valamilyen pozitív egész n-re az állítást már beláttuk. Tekintsünk most egy konvex 3n+1-szöget, és ennek csúcsait jelölje Ai, Bi, Ci, ahol 1≤i≤3n. Az Ai csúcsokat összekötő szakaszokat az indukciós feltevés miatt be tudjuk osztani hármas csoportokba az előírt módon, és ugyanez igaz a Bi csúcsokat összekötő szakaszokra és a Ci csúcsokat összekötő szakaszokra is.
A többi szakaszt pedig a következő módon oszthatjuk be. Alkossanak egy csoportot az AiBj, BjCk és CkAi szakaszok, valahányszor i+j+k osztható 3n-nel; három ilyen szakasz nyilván egy háromszögvonalat alkot. Mivel az i, j, k számok közül bármely kettőt lerögzítve, az oszthatósági feltétel a harmadik számot egyértelműen meghatározza, minden szakasz pontosan egy hármas csoportban fog szerepelni. Ezek szerint az állítás (n+1)-re is igaz, az indukciós lépést befejeztük.
 
III. megoldás (Steller Gábor megoldása alapján). Mint az előző megoldásokban is láttuk, célunk olyan háromszögeket találni, melyek mindhárom csúcsa az eredeti sokszögnek is csúcsa, minden szakasz valamelyik háromszögnek oldala, továbbá minden szakasz csak egy háromszögnek lehet oldala, amit úgy is fogalmazhatunk, hogy bármely két háromszögnek legfeljebb egy közös csúcsa van. Ismét teljes indukciót használunk. Tegyük fel hogy egy P1P2...P3n sokszög esetén már megtaláltuk a keresett PiPjPk háromszögeket, ezek száma a feltételek szerint éppen a szakaszok számának harmada, vagyis
13(3n2n)=3n-1(3n-1)2.

Jelölje egy konvex 3n+1-szög csúcsait Ai, Bi, Ci (1≤i≤3n). Tekintsük az AiBiCi háromszögeket, ahol 1≤i≤3n. Nevezzük ezeket egyes típusú háromszögeknek. Ezen kívül minden, az előző felosztásban szereplő PiPjPk háromszögre készítsük el az AiAjAk, BiBjBk, CiCjCk (kettes típusú) és az AiBjCk, AiCjBk, BiAjCk, BiCjAk, CiAjBk, CiBjAk (hármas típusú) háromszögeket is. Ez éppen
9⋅3n-1(3n-1)2+3n=3n(3n+1-3)2+3n=3n(3n+1-1)2
háromszög, éppen annyi, amennyi az alkalmas felosztáshoz szükséges. Ezért elegendő annyit megmutatni, hogy bármely két fenti háromszögnek legfeljebb egy közös csúcsa van.
Az egyes típusú háromszögeknek nyilván nincs közös csúcsuk, és kettes típusú háromszöggel is csak legfeljebb egy közös csúcsuk lehet. A kettes típusú háromszögeknek vagy nincs közös csúcsuk, vagy az indukciós feltevés miatt legfeljebb egy közös csúcsuk van. A hármas típusú háromszögeket tekintve, ezeknek mind az egyes, mind a kettes típusú háromszögekkel legfeljebb egy közös csúcsa lehet. Végezetül pedig két hármas típusú háromszögnek is csak legfeljebb egy közös csúcsa lehet az indukciós feltevés miatt. Ha ugyanis mondjuk AiBjCk és AiBjCk' is hármas típusú háromszögek, akkor az eredeti 3n-szög felbontásában szerepelnie kellett a PiPjPk és PiPjPk' háromszögeknek is, ami csak k=k' esetén lehetséges.
 
IV. megoldás (Harangi Viktor megoldása alapján). Az általánosság megszorítása nélkül feltehetjük, hogy a sokszög szabályos; ez lehetőséget nyújt egy geometriai jellegű okoskodásra. Ismét n szerinti teljes indukciót alkalmazunk. Ha n=1, akkor az állítás semmitmondó. Tegyük fel, hogy valamely n≥1 esetén a feladatot már megoldottuk, és tekintsünk egy P szabályos 3n+1-szöget. Ennek csúcsait jelöljük meg az A, B, C betűkkel úgy, hogy valamilyen körüljárás szerint végighaladva a sokszög csúcsain, egy A jelű csúcs után mindig B jelű csúcs következzék, B jelű után C jelű, azután pedig ismét A jelű. Az azonos betűvel jelölt csúcsok egy-egy szabályos 3n-szöget alkotnak, melyeknek élei feltevésünk szerint már beoszthatók hármas csoportokra a kívánt módon. Most már csak a különböző jelű csúcsokat összekötő éleket kell beosztani.
Tekintsük a P sokszög egy A jelű csúcsán átmenő t szimmetriatengelyét. Mivel P-nek páratlan sok csúcsa van, ezen nem helyezkedhet el más csúcs. Egy A jelű csúcsot t-re tükrözve ismét A jelű csúcsot kapunk, B jelű csúcsot tükrözve C jelűt kapunk, C jelűt tükrözve pedig B jelű csúcshoz jutunk. Hasonlóképpen B és C jelű csúcsokon átmenő szimmetriatengelyekre való tükrözésnél éppen a B, illetve C jelű csúcsok lesznek azok, amelyek ugyanolyan jelű csúcsba kerülnek.
Konstrukciónk ezek után legyen a következő: egy ABC típusú háromszög élei pontosan akkor alkossanak egy hármas csoportot, ha a háromszög szimmetrikus az A jelű csúcson áthaladó szimmetriatengelyre. Azt állítjuk, hogy ezzel a P sokszög minden AB, BC és CA típusú élét pontosan egyszer használtuk fel, amiből az indukciós lépés helyessége következik.
Valóban, egy AB típusú él pontosan abban az egy háromszögben lesz benne, amelynek harmadik csúcsát úgy kapjuk, hogy a B jelű csúcsot tükrözzük a P sokszög A jelű csúcson áthaladó szimmetriatengelyére; fenti megállapításaink alapján ez éppen egy C jelű csúcs lesz. Szimmetria okok miatt minden AC típusú él is pontosan egy háromszögben lesz benne. Végül egy BC típusú élből kiindulva, tekintsük annak felező merőlegesét. Ez szimmetriatengelye lesz a P sokszögnek, éppen ezért áthalad annak egy jól meghatározott csúcsán, ami a fenti megállapítások miatt csakis A jelű lehet. Ez és csakis ez lehet a keresett háromszög harmadik csúcsa.
 

Végezetül lássuk azt a megoldást, amely rávilágít a feladat valódi geometriai, vagy ha úgy tetszik, algebrai hátterére. A keresett hármas csoportokra való felosztás ugyanis megvalósítható a 3 elemű test feletti n-dimenziós affin tér egyeneseinek segítségével. Hogy ez pontosan mit is jelent, az remélhetőleg kiderül az alábbi gondolatmenetből.
 
V. megoldás (Rácz Béla András megoldása alapján). Legyen p egy tetszőleges prímszám. A következő általános tételt fogjuk bebizonyítani: egy pn szögpontú teljes gráf éleit csoportosítani lehet úgy, hogy az egyes csoportokban lévő élek egy-egy p szögpontú teljes gráf élhalmazát alkossák. Láthatjuk, hogy p=3 esetén ez ekvivalens a kitűzött feladattal.
Tekintsük az a=(a1,a2,...,an) sorozatokat, ahol minden i-re ai p-nél kisebb nemnegatív egész. Ezek száma éppen pn. Ezek lesznek a p elemű test feletti n-dimenziós affin tér pontjai, melyeket az adott teljes gráf szögpontjaival azonosítunk. Ezekre a pontokra egyben vektorként is gondolunk ugyanúgy, ahogyan a 3-dimenziós euklideszi tér pontjait azonosíthatjuk az origóból oda mutató vektorokkal. Az a és v pontok összegén, vagy ha úgy jobban tetszik, az a pont v vektorral való eltoltján az a+v=(a1+v1,a2+v2,...,an+vn) pontot értjük, ahol az ai+vi összegeket moduló p kell tekinteni. Nyilván két pont különbségét is értelmezhetjük hasonló módon, és igaz lesz az, hogy a+(b-a)=b. A v pont (vektor) α-szorosán, ahol α∈{0,1,...,p-1} pedig az αv=(αv1,αv2,...,αvn) pontot (vektort) értjük, ahol természetesen az αvi szorzatokat ismét csak moduló p kell értelmezni. Ezt persze megtehetjük tetszőleges β egész szám esetén is, és ha α és β ugyanolyan maradékot adnak p-vel osztva, akkor nyilván αv és βv ugyanazt a pontot jelöli ki.
Hogyan lehetne értelmezni két különböző a és b ponton átmenő egyenest? Kézenfekvő, hogy az a ponthoz adjuk hozzá a v=b-a vektor skalárszorosait, ahogy azt az euklideszi esetben is tennénk. Nem nehéz megmutatni, hogy minden egyenes p különböző pontból áll. Először is, legfeljebb p pont lehet az egyenesen, hiszen elegendő a v vektor 0,1,...,p-1-szeresét hozzáadni a-hoz. Ha most a+jv=a+kv lenne két különböző j,k∈{0,1,...,p-1} számra, akkor a v vektor minden egyes vi koordinátájára jvi és kvi megegyezne moduló p. Vagyis (k-j)vi osztható lenne p-vel, ami csak úgy lehetséges, ha minden vi=0, ami ellentmond annak, hogy a és b különböző pontok voltak.
Bármely két különböző pont meghatároz tehát egy egyenest, melynek p pontja van. A sorsdöntő észrevétel az, hogy bármely két különböző egyenesnek legfeljebb egy közös pontja van, vagy másképp szólva, bármely két pont pontosan egy egyeneshez tartozik hozzá. Ebből a bizonyítandó állítás már következik: a keresett p szögpontú teljes gráfokat éppen a különböző egyeneseknek feleltethetjük meg.
 
Feladatok
1) Igazoljuk, hogy az a és b pontokon átmenő egyenes meghatározásában a és b szerepe felcserélhető.
2) Igazoljuk, hogy ha c=a+α(b-a) és d=a+β(b-a) az a és b pontok által meghatározott egyenes két különböző pontja, akkor a és b rajta van a c és d pontok által meghatározott egyenesen. Hogyan következik ebből a megoldásban említett ,,sorsdöntő'' észrevétel?
3) Hogyan értelmezhetnénk két egyenes párhuzamosságát?
4) Hogyan lehetne síkokat definiálni? Hány pontja lesz egy síknak? Hogyan nézhet ki két sík közös pontjainak halmaza?
5) Milyen problémákba ütköznénk, ha egy p prímszám helyett egy m összetett számra próbálnánk a fenti tételt és annak bizonyítását átvinni?