| Cím: | A. M. Turing különös világa: A Turing-géptől a rejtjelfejtő Bombe-ig | ||
| Szerző(k): | Dénes Tamás | ||
| Füzet: | 2003/január, 7 - 15. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A. M. Turing születésének 90. évfordulójára emlékezve Alan Mathison Turing éppen kilencven éve született a londoni Paddington-ban 1912. június 23-án. Apja Julius Mathison Turing az Indian Civil Service (Indiai Polgári Szolgálat) tagjaként sokat tartózkodott külföldön. Anyja Ethel Sara Stoney, a Madras vasutak főmérnökének lánya volt, így érthető, hogy Alan szülei Indiában találkoztak és házasodtak össze, de Angliában éltek, így ő is ott született. Amikor Alan egy éves volt, édesanyja követte férjét indiai kiküldetésére, de Alan a család egyik barátjánál maradt Angliában. Beíratták az állami iskolába, de ez nem fejlesztette igazán a kimagasló tehetségű gyereket, ezért néhány hónap múlva otthagyta az iskolát. Ezután a jóval erősebb színvonalú Hazlehurst Preparatory School-ba íratták be, ahol több tantárgyból elnyerte a kiváló tanuló címet. Még az iskolában elkezdett érdeklődni a sakk iránt, ami aztán végigkísérte egész életét. 1926-ban beiratkozott egy patinás középiskolába, a Sherborne School-ba. Ez volt az általános sztrájk éve Angliában, így Turing rendszeresen tett meg 60 mérföldet kerékpáron, otthona és az iskola között. Talán ennek is köszönhette, hogy később versenyszintű atléta vált belőle (hosszútávfutásban ért el kitűnő eredményeket). Turing tehetsége korán kirajzolódott és annak ellenére, hogy tanárai megrótták kézírásáért, angoljáért és azért is, mert a matematikai problémák megoldásában egyéni megoldásokat választott, hamarosan saját útját kezdte járni. Elnyert minden lehetséges matematikai díjat, amit a Sherborne School-ban lehetett. Osztályfőnöke írta Róla: ,,Ha az iskolában van, az a célja, hogy minél többet tanuljon. Ha magában van, feje az iskolában jár.'' Turing már iskolai évei alatt elmélyült a matematikában, ezért tanárai abban támogatták, hogy önmagát képezze, saját elképzelései szerint haladjon. Olvasta Einstein cikkeit a relativitás- elméletről, valamint olvasott a kvantummechanikáról A. S. Eddington (1882‐1944) könyvéből (The nature of the physical world). Turing 1931-ben beiratkozott a cambridge-i King's College matematika szakára. Cambridge sok szempontból könnyebbnek bizonyult az addigi iskoláknál egy olyan ,,renitens'' gondolkodású embernek, mint Turing. Itt kifejthette saját gondolatait, már 1933-ban Russell-t (Introduction to mathematical philosophy), valamint Neumann János írásait olvasta a kvantummechanika matematikájáról. 1933-ban kezdődött Turing érdeklődése a matematikai logika iránt is. Erről így emlékszik a cambridge-i Morel Science Club évkönyve: ,,A. M. Turing elolvasta a Mathematics and Logic című munkát és úgy vélte, hogy a matematika egyszerű logikai megközelítése nem megfelelő.'' Az 1934‐35-ös tanévben hallgatta Max Newman (1897‐1984) előadásait a matematika alapjairól. Ezen a kurzuson foglalkoztak Gödel nemteljességi elméletével és Hilbert eldönthetőségi problémájával (Entscheidungsproblem), melyet a nagy német matematikus, David Hilbert (1862‐1943) vetett fel, részben már az 1900-as Párizsi Nemzetközi Matematikai Kongresszuson (,,Hilbert tizedik problémája''), általánosabb formájában pedig a Bolognai Nemzetközi Matematikai Kongresszuson 1928-ban. Hilbert azt kérdezte, hogy lehetséges-e általános algoritmust adni a matematikai problémák megoldására, vagy egyáltalán létezhet-e elvileg ilyen algoritmus? Igazán nagy jelentőségű lépést e kérdés megválaszolásában egy osztrák matematikus, Kurt Gödel (1906‐1978) 1931-ben bebizonyított tétele jelentett, mely szerint lényegében minden axiómarendszerben megfogalmazható eldönthetetlen állítás, amit az adott axiómarendszer keretein belül sem bizonyítani, sem pedig megcáfolni nem lehet. Első látásra az ,,eldönthetőség'' egyszerű kérdés, hiszen egy adott matematikai állításhoz kell találni egy algoritmust, amelynek segítségével kideríthető, hogy az állítás igaz, vagy hamis. Ekkor kezdett Turing foglalkozni az algoritmus fogalmának pontos meghatározásával. 1937-ben megjelent [8] cikke nagy feltűnést keltett. Ebben a cikkében vezette be az absztrakt gép fogalmát, amelyet máig is Turing-gépnek neveznek. A Turing-gép tulajdonképpen egy ,,darab absztrakt matematika'', és bár elnevezése arra utal, nem technikai eszköz. A Turing-gép, mint minden igazán zseniális elképzelés, könnyen leírható. A szakirodalomban többféle leírás található, mi most az alábbit választottuk. 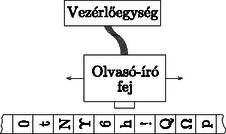 1. ábra Képzeljünk el egy olyan automatát, amely egy végtelen hosszú szalagból, egy ettől független vezérlőegységből, és egy olvasó-író fejből áll. A szalag egymás melletti mezőkre van felosztva, mindegyiken egy-egy jel áll; ezek a jelek egy véges ábécé elemei, és véges sok kivétellel minden mezőn az a speciális jel található, ami az ,,üres'' mezőt jelöli. (A jelek egyike annak a jelölésére szolgál, hogy az illető mező után következő valamennyi mező üres.) Az olvasó-író fej minden lépésben a szalag egyik mezője fölött áll, kezdetben a legelső nem ,,üres'' mezője fölött. A vezérlőegység véges sok állapot valamelyikében van, kezdetben a START állapotban; mindegyik lépésben a fejjel leolvastatja az éppen alatta lévő mező jelét és attól, valamint saját állapotától függően a következőket teszi: átkerül egy másik állapotba, felülíratja az aktuális mezőt, és a fejet az attól eggyel jobbra vagy balra álló mező fölé állítja vagy helyben hagyja. A gép akkor áll meg, amikor vezérlőegysége a STOP állapotba jut. Ebben az absztrakt definícióban benne van a jelek hosszabb jelsorozatokká való összeláncolásának és így tetszőleges bonyolultságú utasítások végrehajtásának és a végrehajtás közben keletkezett jelek (adatok) tárolásának lehetősége. A Turing-gép tehát valójában egy absztrakt automata, amit mai szemmel nagyjából úgy képzelhetünk el, mint egy végtelen nagy tárolókapacitással rendelkező (és bármilyen hosszú ideig futni tudó) ,,célszámítógépet'', mellyel egyetlenegy ,,gyárilag beépített'' program hajtható végre. Eképpen azt is gondolhatjuk, hogy minden, intuitív értelemben vett ,,programnak'' megfelel egy Turing-gép (és viszont). Ez a sok tapasztalattal és elméleti eredménnyel valószínűsített és ezért általánosan elfogadott elképzelés az ún. Church-tézis. Ennek értelmében tehát a Turing-gép tökéletes modellje a program fogalmának. Ugyanekkor Turing definiálta az úgynevezett ,,kiszámítható számot'', mint az olyan valós számot, amelynek akárhányadik tizedesjegye előállítható egy alkalmas Turing-géppel, az üres szalagból kiindulva. Megmutatta például, hogy a kiszámítható, de csak megszámlálhatóan sok ilyen valós szám van, tehát a legtöbb valós szám nem kiszámítható. Turing ezután leírt egy nem kiszámítható számot, megjegyezve, hogy ez paradoxon, hiszen véges sok jellel írt le egy olyan számot, ami ,,nem írható le'' véges számú jellel. Lényegében ugyanezt a paradoxont már 1905-ben felvetette Jules Antoine Richard (1862‐1956) francia matematikus (lásd [1] 165. o.) mint az úgynevezett írógép-paradoxont: Legyenek a halmaz elemei azok a természetes számok, amelyeket (pl. magyar nyelven) leírva legfeljebb 200 billentyűleütéssel tudunk definiálni. Mivel a billentyűk száma véges, a halmaz is véges. Legyen a legkisebb természetes szám, amely nem eleme a halmaznak. Ugyanakkor a ,,legyen az a legkisebb természetes szám, amely nem definiálható magyar nyelven legfeljebb kétszáz billentyűleütéssel'' leírása 200 billentyűleütésnél kevesebbet igényel, ami így nyilvánvaló képtelenség. Turing látta a talált paradoxon feloldásának kulcsát: nem dönthető el (egy másik Turing-gép felhasználásával) hogy egy, akár legfeljebb 200 karakter hosszúságú programot megvalósító Turing-gép kiszámít-e egyáltalán valamit, azaz véges sok lépés után megáll-e. Ezért nincs olyan (a fenti értelemben korlátozott) eljárás, ami tetszőleges természetes számról eldöntené, hogy az kiszámítható-e; így aztán a legkisebb nem kiszámítható természetes szám ebben az értelemben nem számítható ki. (Nem kevésbé fontos a Richard-féle ‐ halmazelméleti ‐ írógépparadoxon feloldása: a látszólagos ellentmondást itt a naiv halmazfogalom tisztázatlansága okozza. A halmaz intuitív fogalmát axiomatikus keretek közé szorítva a paradoxon eltűnik.) Turing-gépekkel kapcsolatos munkásságával megelőzte saját korát, hiszen jóval azelőtt leírta a modern számítógép lényegét, hogy annak technikai feltételei adottak lettek volna. Amíg Turing 1936 és 1938 között Princetonban volt, játszott a gondolattal, hogy tervez egy működő számítógépet. 1938-ban, mikor visszatért Cambridge-be, valóban elkezdett építeni egy analóg mechanikus berendezést a Riemann-hipotézis tanulmányozására (ez a mai napig a matematika egyik leghíresebb megoldatlan problémája). A Riemann-hipotézis a prímszámok számával, illetve azok eloszlásával kapcsolatos, amely problémakör nem csupán a matematikusok fantáziáját mozgatta meg, mivel a hipotézis empirikus ellenőrzése rendkívüli számítási kapacitásokat igényel. Nem véletlen tehát, hogy sokszor a prímszámokkal kapcsolatos problémák inspirálták a számítástechnika fejlődését (lásd [1]). Nem sokkal ezután Turing tevékenysége egészen új fordulatot vett, amikor kapcsolatba került a Government Code and Cypher School-lal (az angol titkosszolgálat rejtjelfejtő szolgálata), akik felkérték, hogy segítsen a német Enigma rejtjelző rendszer feltörésében. Az Enigma egy külsőre írógéphez hasonlító rejtjelző gép volt, melyet Arthur Scherbius német elektromérnök szabadalmaztatott 1918-ban, majd a II. világháborúban a német vezérkar szigorúan titkos üzeneteinek rejtjelzésére használták és tökéletesen megfejthetetlennek tartották. Az Enigma megfejtésére irányuló angol projektet ULTRA-nak nevezték és központja a fenti elnevezésű ,,iskola'' volt, illetve ennek szigorúan titkos körülmények között működő részlegei (lásd [5], [11], [4]). Az ULTRA-ban részt vett három lengyel rejtjelfejtő (Rejewski, Rozycki és Zygalski), akik már 1933-ban elkezdték vizsgálni az Enigma-t. 1938-ban a német megszállás elől Franciaországba menekültek, majd szintén a német megszállás elől Angliába, ahol részt vettek az ULTRA-ban. Ezt az úgynevezett ,,lengyel csoport''-ot nemigen említik az ULTRA történetét feldolgozó írók, pedig jelentőségük meghatározó volt. Amikor kitört a II. világháború, Turing azonnal teljes idejét a Bletchley Park-nak szentelte, ahol az angol titkosszolgálat rejtjelfejtő központja működött. Turing brilliáns ötletei a kódok megfejtésében és az elektronikus számítógép kifejlesztésében nagyban hozzájárultak az Enigma rendszer feltöréséhez, melynek eredményeként sok-sok emberi életet sikerült megmenteni. Paradox módon, eme időszak nagyon boldog periódusa volt életének, melyről Newman így ír: ,,Talán életének legboldogabb időszaka volt, amelyben legjobban kamatoztathatta sziporkázó kreativitását.'' W. G. Welchmannal együtt Turing, a ,,lengyel csoport'' korábbi munkájára alapozva, megtervezte azt a rejtjelző gépet, amely 1940 végétől dekódolta az összes üzenetet, amelyet a német légierő az Enigmával rejtjelezve küldött. Ezt a berendezést Bombe-nak nevezték el (lásd a címlapot). A német haditengerészet Enigma rejtjelző gépének feltörése jóval nehezebb feladatnak bizonyult, azonban éppen ez a kihívás volt az, ami Turingot legjobban vonzotta. 1941 közepén Turing statisztikus módszere az elfogott rejtjeles üzenetek feldolgozásával lehetővé tette a német haditengerészet rejtjeles üzeneteinek gyakorlatilag a német vezérkarral egyidőben való megfejtését. Ezt a Bletchley Park nagy sikereként tartja számon a történelem. Kevesebb szó esik azonban arról a Turing által vezetett tevékenységről, amely a világ első elektronikus számítógépének, a Colossus-nak létrehozása volt. A szűkszavúság annak köszönhető, hogy a Colossus megtervezése, létrehozása és főleg üzemeltetése (szinte csak rejtjelzési és rejtjelfejtési feladatokra használták!) szigorúan titkos körülmények között történt, olyannyira, hogy csupán néhány eredeti fénykép készült róla. A háború befejeztével számítógéptervezés feladatával hívták meg a londoni National Physical Laboratory-ba. Erre vonatkozó tervjavaslatát Automatic Computing Engine (ACE) címmel 1946 márciusában adta le. A Colossus megépítésének tapasztalatai után ma már érthető a magyarázat a gyorsan elkészült tervekre. Nem csoda tehát, hogy Turing eredeti, részletekbe menő és számos rajzmelléklettel gazdagon illusztrált dokumentációja igazi modern számítógépet mutatott be. Ugyanakkor az ACE tervezett memória-méreteit túlzottnak tartották a döntéshozók, így ez a terv megvalósítását késleltette. Turing 1947-ben visszatért Cambridge-be, ahol olyan, a számítógépektől és a matematikától látszólag távoli területeket kezdett tanulmányozni, mint a neurológia és a pszichológia. De ez alatt sem nem feledkezett el a számítógépekről, számítógépes programozási ,,kódokat'' készített. Turing a háború után komolyan foglalkozott a tudományon kívüli világgal is. Tagja volt a Walton Athletic Club-nak és rekordidővel nyerte a 3 és 10 mérföldes futóbajnokságot. 1947-ben maratoni futásban is negyedik helyezett lett. 1948-ban Newman a University of Manchester matematika professzoraként állást ajánlott Turingnak, amit ő el is fogadott. 1950-ben publikálta Computing machinery and intelligence című cikkét a Mind folyóiratban [10], amelyet életművének kiemelkedő teljesítményeként tart számon a mai tudomány. Ebben a cikkében a mesterséges és természetes intelligencia legmélyebb problémáit vizsgálta. Itt írta le az általa javasolt és az ő nevét viselő tesztet, amely a mesterséges és természetes intelligencia megkülönböztetését helyezte egzakt alapokra. A. M. Turing a mesterséges intelligencia kutatások előfutárának is tekinthető, ő vetette fel elsőként azt, hogy mit is jelent a ,,gépi intelligencia''. Az első megválaszolásra váró kérdés persze az volt, hogy létezik-e ilyesmi, hiszen máig tartja magát az a többségi felfogás, hogy intelligenciával csupán az ember rendelkezik, ezért a ,,gépi intelligencia'' szóösszetétel értelmetlen. Turing azt is látta, hogy az intelligencia és gondolkodás fogalmai elválaszthatatlanok egymástól, ezért fogalmazta meg 1950-ben megjelent, klasszikussá vált cikkében egyetlen mondatba sűrített kérdését: ,, tudnak-e a gépek gondolkodni?'' Turing szerint a ,,gondolkodni'' szó inkább érzelmi kérdéssé teszi e problémakört, ezért el is veti, mint túlságosan bizonytalan (szubjektív) fogalmat. Ugyanakkor az 1950-es években sokan úgy gondolták, hogy Kurt Gödel nemteljességi tétele a mesterséges intelligencia lehetetlenségét is bizonyítja: A mesterséges intelligencia mindig ,,egy program'', azaz egy Turing-gép (Church-tézis). Az ebben a gépben tárolt axiómarendszer meghatároz egy ,,nyelvet'', amelyen megfogalmazható olyan kérdés, amelyre ebben az axiómarendszerben nem vezethető le igen-nem jellegű válasz (Gödel-tétel). Tehát e mesterséges intelligencia számára érthető nyelven megfogalmazható olyan kérdés, amelyre az nem tud sem igennel, sem nemmel válaszolni! Bár ez az érvelés több sebből vérzik, csupán egyet emelek ki ezek közül: Ha a mesterséges intelligenciát, mint az emberi intelligenciát utánzó konstrukciót fogjuk fel, akkor ennek megvalósíthatatlanságát nem bizonyítja az az érv, hogy bizonyos kérdésekre nem tud egyértelműen felelni, hiszen ez az emberi gondolkodásnak is jellemzője. A rekurzív függvények elméletének, a matematikai nyelvészetnek jelentős alakja, a magyarországi kibernetikai iskola megalapítója, Kalmár László (1905‐1976) az 1948-as amszterdami Filozófiai kongresszuson tartott előadásában bebizonyította, hogy a Church-tézis a Gödel-tételből levezethető, így nem bizonyíthatja abszolút eldönthetetlen probléma létezését. Kalmár László hangsúlyozta, hogy ezeket a tételeket (Gödel, Church) szabatosan úgy kellene megfogalmazni, hogy a kérdéses problémasereg általános rekurzív eljárással nem oldható meg, nem pedig abszolút megoldhatatlanságról beszélni (lásd [6], [7]). Turingot az ellenvetések és főleg a ,,gépi intelligencia'' fogalmának bizonytalansága csak inspirálta egy új megközelítés felvetésére. Ennek lényege, hogy a szubjektív és tudományosan megfoghatatlan fogalmak helyett olyan módszert kell konstruálni, amelyet jól definiált technikai fogalmakkal lehet leírni. Ezt, az általa ,,utánzási játéknak'' nevezett módszert manapság Turing-teszt, vagy Turing-próba néven ismerjük. A Turing-teszt lényege (lásd 2. ábra): Képzeljük el, hogy egy C számítógép és egy E ember két külön helyiségben van és mindketten elektronikus kapcsolatban vannak egy harmadik helyiségben levő K személlyel, aki elektronikus úton kérdéseket tehet fel mindkettejüknek. K-nak az a célja, hogy a kérdéseire érkező válaszok alapján meg tudja különböztetni, hogy melyik válasz származik C-től és melyik E-től. 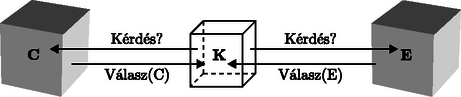 2. ábra. A Turing-teszt vázlata A teszt egyik óriási előnye, hogy ‐ az intelligenciáról, gondolkodásról való elmeélesítő gondolatkísérletek helyett ‐ a gyakorlatban kivitelezhető és a probléma lényegét megragadó eszközt ad a kezünkbe. Hiszen most már az eredeti helyett azzal a jól kezelhető kérdéssel állunk szemben, hogy ,,van-e olyan gép, amely ezt a játékot jól tudja játszani?'' A mesterséges intelligencia kutatások célkitűzése tehát a gépek alkalmassá tétele arra, hogy az embert minél pontosabban tudják utánozni. Ebben a korszakos cikkében Turing kifejezte meggyőződését, hogy a XX. század végére a gépek már elég jól fogják játszani ezt a játékot ahhoz, hogy egy átlagos kérdezőnek nem lesz 70%-nál több esélye az azonosításra 5 percnyi kérdezés után. Turingot a Royal Society of London 1951-ben tagjává választotta, alapvetően a Turing-gépekre vonatkozó munkásságának elismeréseként. 1951‐52-ben a matematika biológiai alkalmazásaival, az élő organizmusok modellezésének kutatásával foglalkozott. A GCHQ-nak (az angol titkosszolgálatnak) a hidegháborús évek alatt is a rejtjelfejtő műveleti csoport tevékenysége állt a középpontjában, melynek bázisa a Bletchley Park volt. Itt folytatta tevékenységét Turing a továbbiakban is, bár manchesteri kollégái erről mit sem sejtettek. Turing 1954. június 7-én kálium-cianid mérgezésben halt meg, amikor éppen egy elektrolízis kísérleten dolgozott. A mérget egy félig elfogyasztott almában találták meg mellette. A nyomozás önkezűséget állapított meg, de édesanyja meg volt győződve arról, hogy baleset történt. A Turing-teszt napjaink e-kommunikációjában Vajon ha A. M. Turing megérte volna éppen 2002-ben esedékes 90. születésnapját, hogyan látná saját ötven évvel ezelőtti elképzeléseit? Valószínűleg elismerné, hogy a fantáziája nem volt elegendő ahhoz, hogy előre lássa azt a technikai robbanást, amely a számítástechnikában, elektronikában, kommunikáció-technológiában bekövetkezett, s amelynek eredményeként a jelenünk, mindennapjaink részévé, napi gyakorlattá vált a Turing-teszt. A mai információ alapú társadalom ugyanis egy ún. ,,fekete doboz'' modellt valósít meg. Ebben a modellben (lásd 3. ábra) egy óriási információtárolóval (ez a ,,fekete doboz'') kommunikál minden felhasználó úgy, hogy a felhasználók egymás számára valójában ismeretlenek és csak a ,,fekete doboz''-hoz való csatlakozás követel meg egyszerűbb, vagy szigorúbb azonosítást (,,bemutatkozást''). Ma az internet egyik fő vonzereje a ,,globális névtelenség'', ami egyúttal számos visszaélés és bűncselekmény forrása is. A modell tehát úgy működik, hogy mindenki (személy, cég, intézmény stb.) egy közös dobozba (,,fekete doboz'') juttatja el az információit, és ebből mindenki annyit vehet ki, amennyire a ,,fekete doboz'' engedélyt ad. 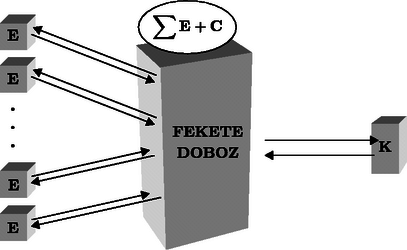 3. ábra. Globális kommunikáció modellje A 3. ábra globális kommunikációs modellje pontosan úgy néz ki, mint egy megsokszorozott Turing-modell, ahol mindenki a géppel kommunikál elektronikusan, így mindenki lehet kérdező (K) és kérdezett (E), a gép pedig összegyűjti és tárolja a információt. A. M. Turing idézett 1950-es cikkében tesztjét így fogalmazta meg: ,,Azt állíthatjuk, hogy egy gép gondolkodik, ha kérdéseket tehetünk fel neki, éspedig tetszőleges kérdéseket és az úgy válaszol, hogy ha nem ,,nézünk oda'', nem tudjuk, hogy a felelet géptől, vagy embertől származik-e.'' Turing gondolatmenete látnoki volt, ugyanis tökéletesen illeszkedik a jelen e-társadalmának 3. ábrán felvázolt globális kommunikációs hálózataira. A kommunikációs hálózat minden felhasználója () valóban egy monitor előtt ül és kérdéseket tesz fel. A monitoron megjelenő válaszok tartalmából azonban nem dönthető el biztosan a válaszoló ,,személye'', így annak valódi, vagy virtuális volta sem! A titkolódzás az e-kommunikációban általánossá válik, kilép a titkosszolgálatok szűk világából és mindennapjaink része lesz. Egyre nyilvánvalóbb a ,,nyíltan titkolódzás'' szükségessége, amely ,,paradox játék'' nagyon hasonlít a Turing-tesztre, sőt mára önálló területté vált a kriptográfiában, ez a ,,zero-knowledge proof'', azaz az ,,előismeretek nélküli bizonyítás''. A probléma megfogalmazása igen egyszerű, ha észrevesszük, hogy a globális kommunikáció 3. ábra szerinti modelljében a szerepek felcserélhetők, azaz bárki lehet kérdező és kérdezett, valamint fenti gondolatmenetünk szerint a gép és a számtalan felhasználó sem különböztethető meg. Tételezzük fel, hogy a ,,fekete dobozban'' egy labirintus van, amely egy titkos ajtót rejt, amelyen mindenképpen át kell jutni ahhoz, hogy a labirintus egyik feléből a másikba jussunk (lásd 4. ábra). A B játékos ismeri az ajtó titkát (ki tudja nyitni azt!), de úgy kell ezt bebizonyítania az A játékosnak, hogy közben magát a titkot ne árulja el. Ezt nevezi a nemzetközi szakirodalom ,,zero-knowledge proof''-nak, azokat az eljárásokat pedig, amelyek alkalmasak az ilyenfajta bizonyításra, ,,zero-knowledge protocol''-nak. 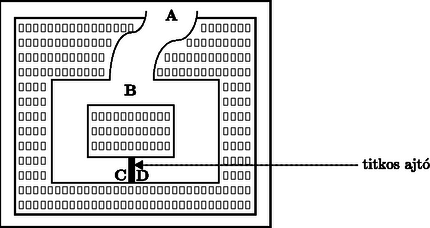 4. ábra. Labirintus titkos ajtóval Íme egy általános eljárás (protokoll) az előismeret nélküli bizonyításra:
Így a B játékos bebizonyítja, hogy ismeri a titkot, de A-nak mégsem kell elárulnia azt. Ha csak egyszer játsszák el a 2.‐3. lépéseket (), akkor az A játékos bizalmatlanul mondhatná, hogy valószínűséggel, véletlenül is kerülhetett a titkos ajtó megfelelő oldalára a B játékos. Ha azonban 10-szer, vagy akár 20-szor ismétlik meg a 2.‐3. lépéseket, akkor már mindössze vagy a tévedés valószínűsége. A ,,zero-knowledge protocol''-ok jelentősége egyre nyilvánvalóbb, így a szakirodalomban és a gyakorlati információ-védelemben is egyre nagyobb szerepet töltenek be. Könnyen belátható, hogy ilyen ,,labirintus'' szituációban vagyunk minden bankautomatánál, kártyával történő fizetéskor, telefonálás közben, vagy amikor belépünk az e-mail boxunkba. Hivatkozások jegyzéke
 |