Cím:	A 33. Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):	Gnädig Péter ,  Honyek Gyula ,  Szegedi Ervin
Füzet:	2002/november, 492 - 500. oldal	PDF  |  MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1   Honyek Gyula ‐ Szegedi Ervin ‐ Gnädig Péter   Elméleti forduló   1. feladat. Földbe hatoló radar   1. A hullám $v$ fázissebességét (az azonos fázisú helyzetek haladási sebességét) az $\begin{array}{c}{\displaystyle \omega t-\beta z=\text{állandó}\mathrm{,}\text{azaz}\omega \Delta t-\beta \Delta z=0}\end{array}$ összefüggés határozza meg. Innen $\begin{array}{c}{\displaystyle v=\frac{\Delta z}{\Delta t}=\frac{\omega }{\beta }=\frac{1}{\sqrt[]{\frac{\mu \epsilon }{2}\left(\sqrt[]{1+\frac{{\sigma }^2}{{\epsilon }^2{\omega }^2}}+1\right)}}\approx \frac{1}{\sqrt[]{\mu \epsilon }}\mathrm{.}}\end{array}$   Megjegyzések. (i) A fentebb kiszámított fázissebesség ‐ az adott közelítésben ‐ független a hullám frekvenciájától, és alakilag a fény terjedési sebességével egyezik meg. (Természetesen a látható fény frekvenciatartományában a képlet nem érvényes.) (ii) A radarhullámok nem végtelen síkhullámok, hanem térben és időben korlátozott kiterjedésű hullám-vonulatok (hullámcsomagok). Ezek terjedését nem a fázissebesség, hanem az ún. csoportsebesség jellemzi, amely a $\beta \left(\omega \right)$ függvény differenciálhányadosának reciproka, és a nagysága általában különbözik a fázissebességtől. Amennyiben $\beta$ arányos $\omega$-val (a feladatban használható közelítésben ez teljesül), a kétféle sebesség megegyezik. 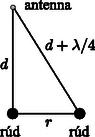  2. A földbe hatoló hullámok érzékelhetőségi távolságára jellemző ,,behatolási mélység'' (vagyis az a mélység, ahol a hullám amplitúdója a felszíni érték $1/e\approx 0\mathrm{,}37$-szerese) az $\alpha$ a csillapodási együttható reciproka: $\begin{array}{c}{\displaystyle \delta =\frac{1}{\alpha }=\frac{1}{\omega \sqrt[]{\frac{\mu \epsilon }{2}\left(\sqrt[]{1+\frac{{\sigma }^2}{{\epsilon }^2{\omega }^2}}-1\right)}}\approx \frac{1}{\omega \sqrt[]{\frac{\mu \epsilon }{2}\left[\left(1+\frac{{\sigma }^2}{2{\epsilon }^2{\omega }^2}\right)-1\right]}}=\frac{2}{\sigma }\sqrt[]{\frac{\epsilon }{\mu }}\approx 16\text{m. }}\end{array}$     1. ábra   3. A rudakról visszaverődő hullámok fáziskülönbsége akkor lesz ${180}^{\circ }$, ha az egyik rúd és a műszer távolsága éppen egy negyed hullámhossznyival nagyobb, mint a másik rúd és a műszer távolsága. Az 1. ábrán látható helyzetben tehát fennáll $\begin{array}{c}{\displaystyle r^2+d^2={\left(d+\frac{\lambda }{4}\right)}^2\mathrm{,}}\end{array}$ ahonnan ${\lambda }^2+4\lambda d-4r^2=0$, melynek megoldása $\lambda =12\mathrm{,}5$cm. A hullám terjedési sebessége a megadott számadatokból $v=1\mathrm{,}0\cdot {10}^{10}$cm/s, a kérdéses frekvencia tehát 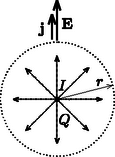$\begin{array}{c}{\displaystyle f_{\underset{}{\overset{}{\text{min}}}}=\frac{v}{\lambda }=800\text{MHz}\mathrm{.}}\end{array}$   4. Ha a detektor a rúdhoz legközelebbi helyzettől $x$ távolságra van, akkor a radarimpulzusok visszaérkezési ideje a $d$ mélységben fekvő rúdról $\begin{array}{c}{\displaystyle t\left(x\right)=2\frac{\sqrt[]{d^2+x^2}}{v}\ge t_{\underset{}{\overset{}{\text{min}}}}=\frac{2d}{v}\mathrm{.}}\end{array}$ Innen $\begin{array}{c}{\displaystyle d=\frac{v{t}_{\underset{}{\overset{}{\text{min}}}}}{2}=5\text{m}\mathrm{.}}\end{array}$   2. feladat. Elektromos jelek érzékelése       2. ábra   1. Ha egy gömb alakú, kicsiny elektródából homogén és végtelen közegben $I$ állandó áram folyik ki, akkor a szimmetria miatt nyilvánvaló, hogy az áramsűrűség csak az elektródától mért távolságtól függ, az iránytól nem. A töltésmegmaradás miatt egy tetszőleges $r$ sugarú, elektróda középpontú gömbfelületen $I$ áram folyik ki át (2. ábra), ezért $\begin{array}{c}{\displaystyle j=\frac{I}{4\pi r^2}\mathrm{,}}\end{array}$ vagy az irányokat is figyelembe véve $\begin{array}{c}{\displaystyle \text{j}=\frac{I}{4\pi r^3}\text{r}\mathrm{.}}\end{array}$   2. Ha az előzőekben vizsgált szituációban a közeg fajlagos ellenállása $\varrho$, akkor a differenciális Ohm-törvény alapján az elektróda által létrehozott elektromos térerősség az $\text{r}$ helyvektorú pontban 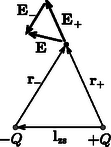$\begin{array}{c}{\displaystyle \text{E}=\varrho \cdot \text{j}=\frac{I\varrho }{4\pi r^3}\text{r}\mathrm{.}}\end{array}$ Vegyük észre, hogy ez az elektromos mező egy $Q={\epsilon }_0\varrho I$ nagyságú pontszerű töltés, vagy egy töltött gömb (gömbön kívüli) elektromos terével egyezik meg.     3. ábra   Tekintsük most a feladatban leírt esetet! A zsákmány belsejében elképzelt két, egymástól viszonylag távol lévő gömb egyikéből $I_{\text{zs}}$ áram folyik ki, a másik gömbbe pedig $I_{\text{zs}}$ áram folyik be. A gömbök között végtelen, homogén, $\varrho$ fajlagos ellenállású közeg van. A kialakuló elektromos mező és árameloszlás (az elektromos mezőt leíró egyenletek linearitása miatt) felfogható úgy, mint egy végtelen, homogén közegben elhelyezkedő $+Q$ töltésű és egy tőle $l_{\text{zs}}$ távolságra levő $-Q$ töltésű gömbelektróda elektromos és áramterének lineáris szuperpozíciója. A 3. ábra jelöléseivel az egyes mezők térerősségei és potenciáljai: $\begin{array}{c}{\displaystyle {\text{E}}_{+}=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{r_{+}^3}{\text{r}}_{+}=\frac{\varrho I_{\text{zs}}}{4\pi r_{+}^3}{\text{r}}_{+}\mathrm{,}{U}_{+}=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{r_{+}}=\frac{\varrho I_{\text{zs}}}{4\pi r_{+}}\mathrm{,}}\end{array}$ illetve $\begin{array}{c}{\displaystyle {\text{E}}_{-}=\frac{1}{4\pi {\epsilon }_0}\frac{\left(-Q\right)}{r_{-}^3}{\text{r}}_{-}=-\frac{\varrho I_{\text{zs}}}{4\pi r_{-}^3}{\text{r}}_{-}\mathrm{,}{U}_{-}=\frac{1}{4\pi {\epsilon }_0}\frac{\left(-Q\right)}{r_{-}}=-\frac{\varrho I_{\text{zs}}}{4\pi r_{-}}\mathrm{.}}\end{array}$ A szuperpozíció eredménye: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{E}}& {\displaystyle ={\text{E}}_{+}+{\text{E}}_{-}=\frac{\varrho I_{\text{zs}}}{4\pi }\left(\frac{{\text{r}}_{+}}{r_{+}^3}-\frac{{\text{r}}_{-}}{r_{-}^3}\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle U}& {\displaystyle =U_{+}+U_{-}=\frac{\varrho I_{\text{zs}}}{4\pi }\left(\frac{1}{r_{+}}-\frac{1}{r_{-}}\right)\mathrm{.}}\hfill \end{array}}}\end{array}$ A feladatban vizsgálandó $P$ pontban $r_{+}=r_{-}=r$, valamint ${\text{r}}_{+}-{\text{r}}_{-}={\text{l}}_{\text{zs}}$, ezért a ragadozó helyén az elektromos térerősség $\begin{array}{c}{\displaystyle {\text{E}}_P=\frac{\varrho I_{\text{zs}}}{4\pi r^3}{\text{l}}_{\text{zs}}\mathrm{.}}\end{array}$ Felhasználva, hogy $r\approx y$, $\begin{array}{c}{\displaystyle {\text{E}}_P=\frac{\varrho I_{\text{zs}}}{4\pi y^3}{\text{l}}_{\text{zs}}\mathrm{.}}\end{array}$   3. Jelölje a zsákmányállatot modellező két gömb alakú áramforrás közül a negatív elektróda potenciálját $U_x$, a pozitív elektródáét pedig $U_y$. Ezek a potenciálok az általános képlet segítségével az $r_{\text{zs}}$ sugarú elektródák felületén is meghatározható: $\begin{array}{c}{\displaystyle U_x=\frac{\varrho I_{\text{zs}}}{4\pi }\left(\frac{1}{l_{\text{zs}}-r_{\text{zs}}}-\frac{1}{r_{\text{zs}}}\right)\mathrm{,}{U}_y=\frac{\varrho I_{\text{zs}}}{4\pi }\left(\frac{1}{r_{\text{zs}}}-\frac{1}{l_{\text{zs}}-r_{\text{zs}}}\right)}\end{array}$ Az elektródák közötti $U_{\text{zs}}$ feszültség a potenciálok különbségeként kapható: $\begin{array}{c}{\displaystyle U_{\text{zs}}=U_y-U_x=\frac{\varrho I_{\text{zs}}}{2\pi r_{\text{zs}}}\frac{l_{\text{zs}}-2r_{\text{zs}}}{l_{\text{zs}}-r_{\text{zs}}}\mathrm{.}}\end{array}$ Felhasználva, hogy $r_{\text{zs}}\ll l_{\text{zs}}$, a zsákmányban elképzelt forrásgömbök közötti feszültség: $\begin{array}{c}{\displaystyle U_{\text{zs}}=\frac{\varrho I_{\text{zs}}}{2\pi r_{\text{zs}}}\mathrm{.}}\end{array}$ A forrásgömbök közötti $R_{\text{zs}}$ ellenállás, és a forrás $P_{\text{zs}}$ teljesítménye könnyen kaphatók: $\begin{array}{c}{\displaystyle R_{\text{zs}}=\frac{U_{\text{zs}}}{I_{\text{zs}}}=\frac{\varrho }{2\pi r_{\text{zs}}}\mathrm{,}{P}_{\text{zs}}=U_{\text{zs}}{I}_{\text{zs}}=\frac{\varrho I_{\text{zs}}^2}{2\pi r_{\text{zs}}}\mathrm{.}}\end{array}$   4. A zsákmány által keltett elektromos mező homogénnek tekinthető a ragadozó helyén, térerőssége a korábban meghatározott ${\text{E}}_P$, ezért a helyettesítő kapcsolásban $U$-val jelölt feszültség: $\begin{array}{c}{\displaystyle U=E_{\text{r}}{l}_{\text{d}}=\frac{\varrho I_{\text{zs}}}{4\pi y^3}{l}_{\text{zs}}{l}_{\text{d}}\mathrm{,}}\end{array}$ ahol $l_{\text{d}}$ a ragadozó érzékelő (detektáló) gömbjeinek távolságát jelöli, a gömbök sugara pedig $r_{\text{d}}$ $\left(r_{\text{d}}\ll l_{\text{d}}\right)$. A környező tengervíz $R_{\text{v}}$ ellenállása az $R_{\text{zs}}$-vel való analógia alapján: $\begin{array}{c}{\displaystyle R_{\text{v}}=\frac{\varrho }{2\pi r_{\text{d}}}\mathrm{.}}\end{array}$ A modellben szereplő soros kapcsolású áramkörben a kérdezett $U_{\text{d}}$ feszültség és $P_{\text{d}}$ teljesítmény egyszerűen számolható: $\begin{array}{c}{\displaystyle U_{\text{d}}=U\frac{R_{\text{d}}}{R_{\text{d}}+R_{\text{v}}}=\frac{\varrho I_{\text{zs}}}{4\pi y^3}{l}_{\text{zs}}{l}_{\text{d}}\frac{R_{\text{d}}}{R_{\text{d}}+\frac{\varrho }{2\pi r_{\text{d}}}}\mathrm{,}}\end{array}$ illetve $\begin{array}{c}{\displaystyle P_{\text{d}}=\frac{U_{\text{d}}^2}{R_{\text{d}}}={\left(\frac{\varrho I_{\text{zs}}}{4\pi y^3}{l}_{\text{zs}}{l}_{\text{d}}\right)}^2\frac{R_{\text{d}}}{{\left(R_{\text{d}}+\frac{\varrho }{2\pi r_{\text{d}}}\right)}^2}\mathrm{.}}\end{array}$   Megjegyzés. Az áramkör helyettesítő kapcsolása alapján megállapíthatjuk, hogy az elrendezés éppen olyan, mintha egy $U$ elektromotoros erejű, $R_{\text{v}}$ belső ellenállású feszültségforrásra $R_{\text{d}}$ nagyságú terhelő ellenállást kötöttünk volna. Jóllehet a verseny során a résztvevőktől nem kérték annak belátását, hogy a rendszer (vagyis a ragadozó + zsákmány + tengervíz) elektromos szempontból a megadott áramkörrel helyettesíthető, de ,,versenyen kívül'' tanulságos lehet ennek végiggondolása. Induljunk ki abból a helyzetből, amelyben a ragadozó halon még nem tud áram folyni (mondjuk azért, mert a hal ,,kikapcsolta'' a detektáló egységét, vagyis annak belső ellenállása végtelen nagy). A hal közelében $E_{\text{r}}$ az elektromos térerősség, az egymástól $l_{\text{d}}$ távol levő érzékelői között tehát $U=E_{\text{r}}{l}_{\text{d}}$ feszültség alakul ki. Kapcsoljuk most be a hal detektáló egységét, csökkentsük le a hal belső ellenállását a megadott $R_{\text{d}}$ értékre! Ekkor a halon keresztül valamekkora $I$ áram indul meg, s ez a ragadozó halat modellező két gömböt elektromosan töltötté teszi (az egyik pozitív, a másik negatív töltésű lesz). Ha nem lenne a környező tengervíz, akkor a hal testében folyó áramnak ‐ a töltésmegmaradás törvénye miatt ‐ előbb-utóbb meg kellene szűnnie. Ilyen esetben tehát a gömbök feltöltődése csak addig tarthatna, amíg az feltöltődés következtében kialakuló elektromos erőtér a külső erőtérrel együtt éppen nulla potenciálkülönbséget eredményez a két gömb között. Más a helyzet azonban akkor, amikor a hal testén átáramló töltések a környező tengervízben vissza tudnak jutni az eredeti helyükre. Ekkor folyamatos $I$ áram alakul ki, a halra (a modellben a két gömbre) jutó $U_{\text{d}}$ feszültség pedig nullától különböző lesz. Ez a feszültség kétféle módon is kiszámítható. Egyrészt úgy, mint $\begin{array}{c}{\displaystyle U_{\text{d}}=I{R}_{\text{d}}}\end{array}$ (Ohm-törvény). Másrészt úgy is megkapható, mint az eredő elektromos térerősségnek (vagyis a zsákmány által a ragadozó helyén létrehozott ,,külső'' $E_{\text{r}}$ és a gömbök feltöltődése miatt kialakuló $E_1$ különbségének) és az $l_{\text{d}}$ távolságnak a szorzata: $\begin{array}{c}{\displaystyle U_{\text{d}}=\left(E_{\text{r}}-E_1\right)l_{\text{d}}\mathrm{.}}\end{array}$ A jobb oldalon a zárójelet felbontva az első tag éppen a külső erőtér által létrehozott $U$ feszültséggel egyezik meg, a második tag pedig kifejezhető a környező tengervíz ,,effektív ellenállásával'': $\begin{array}{c}{\displaystyle E_1{l}_{\text{d}}=I{R}_{\text{v}}\mathrm{.}}\end{array}$ Mindezeket összevetve végül felírhatjuk, hogy $U-I{R}_{\text{v}}=I{R}_{\text{d}}\mathrm{,}$ s ez valóban a megadott helyettesítő kapcsolás feszültség-áram viszonyainak felel meg.   5. Az $R_{\text{d}}$ függvényében vizsgált $P_{\text{d}}$ teljesítmény akkor maximális, ha az $\begin{array}{c}{\displaystyle \frac{R_{\text{d}}}{{\left(R_{\text{d}}+\frac{\varrho }{2\pi r_{\text{d}}}\right)}^2}}\end{array}$ kifejezés maximális, vagy ennek reciproka minimális. Közismert, hogy ez $\begin{array}{c}{\displaystyle R_{\text{d}}=R_{\text{v}}=\frac{\varrho }{2\pi r_{\text{d}}}}\end{array}$ esetén következik be (vagyis akkor, amikor a ,,telepet'' éppen a ,,belső ellenállásával'' egyenlő nagyságú ellenállással terheljük). Ezt például a számtani és a mértani közép közötti egyenlőtlenség felhasználásával, vagy deriválással láthatjuk be. $P_{\text{d}}$ maximuma behelyettesítéssel kapható: $\begin{array}{c}{\displaystyle P_{\text{d}}^{\text{(max)}}=\frac{\varrho {\left(I_{\text{zs}}{l}_{\text{zs}}{l}_{\text{d}}\right)}^2{r}_{\text{d}}}{32\pi y^6}\mathrm{.}}\end{array}$   3. feladat. Lejtős úton mozgó nehéz jármű   1. Egy-egy kerék tehetetlenségi nyomatékának meghatározása Egy 0,025 $M$ tömegű, 0,8 $R$ sugarú küllő tehetetlenségi nyomatéka (a végpontjára vonatkoztatva) az ismert $\Theta =m{l}^2/3$ elméleti formula alapján ${\Theta }_{\text{<span style="font-size:10px;">küllő</span>}}=5\mathrm{,}33\cdot {10}^{-3}M{R}^2$. A kerék hengeres részének tehetetlenségi nyomatéka a tömör henger és a lyukat kitöltő tömör henger tehetetlenségi nyomatékának különbségeként számolható. A tömeg- és területarányok egyenlősége alapján kapható, hogy $m_{\text{<span style="font-size:10px;">tömör</span>}}=2\mathrm{,}22M$, $m_{\text{<span style="font-size:10px;">lyuk</span>}}=1\mathrm{,}42M$, a sugarak pedig $0\mathrm{,}8R$ és $R$. Felhasználva, hogy egy tömör henger esetén $\Theta =m{R}^2/2$, a vizsgált henger tehetetlenségi nyomatéka ${\Theta }_{\text{<span style="font-size:10px;">henger</span>}}={\Theta }_{\text{<span style="font-size:10px;">tömör</span>}}-{\Theta }_{\text{<span style="font-size:10px;">lyuk</span>}}=\frac{1}{2}\left[m_{\text{<span style="font-size:10px;">tömör</span>}}{R}^2-m_{\text{<span style="font-size:10px;">lyuk</span>}}{\left(0\mathrm{,}8R\right)}^2\right]=0\mathrm{,}656M{R}^2\mathrm{,}$ a kerék egészének tehetetlenségi nyomatéka pedig: $\Theta ={\Theta }_{\text{<span style="font-size:10px;">henger</span>}}+8{\Theta }_{\text{<span style="font-size:10px;">küllő</span>}}=0\mathrm{,}699M{R}^2\approx 0\mathrm{,}7M{R}^2\mathrm{.}$   2. A mozgásegyenletek Az $5M$ tömegű kocsitestre a nehézségi erő és a kerekek (azok forgástengelye) által kifejtett erő hat. 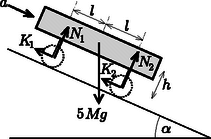    4. ábra   A kerekek által kifejtett erőket célszerű lejtővel párhuzamos és arra merőleges komponensekre bontani. Mivel a kocsitest a lejtőn lefelé haladva gyorsul, de nem forog, mozgásegyenletei a 4. ábra jelöléseivel a következő alakba írhatók: $\begin{array}{c}{\displaystyle 5Ma=5Mg\text{sin}\alpha -K_1-K_2\mathrm{,}}\end{array}$ (1) $\begin{array}{c}{\displaystyle 5Mg\text{cos}\alpha =N_1+N_2\mathrm{,}}\end{array}$ (2) $\begin{array}{c}{\displaystyle N_{2}l=N_{1}l+K_{1}h+K_{2}h\mathrm{.}}\end{array}$ (3) Az $M$ tömegű, $R$ sugarú, $0\mathrm{,}7M{R}^2$ tehetetlenségi nyomatékú hátsó kerékre a gravitációs erőn túl tengelynél a kocsitest, a talajjal érintkező pontban pedig a lejtő fejt ki erőt (5. ábra). A kerék tömegközéppontjának gyorsulása $a$, a szöggyorsulást pedig jelölje ${\beta }_1$. A kerék mozgásegyenletei: 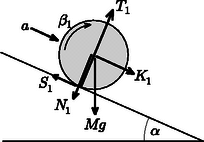$\begin{array}{c}{\displaystyle Ma=K_1-S_1\mathrm{,}}\end{array}$ (4) $\begin{array}{c}{\displaystyle Mg\text{cos}\alpha +N_1=T_1\mathrm{,}}\end{array}$ (5) $\begin{array}{c}{\displaystyle 0\mathrm{,}7M{R}^2{\beta }_1=S_{1}R\mathrm{.}}\end{array}$ (6) Ha a hátsó kerék tisztán gördül, akkor: $\begin{array}{c}{\displaystyle a=R{\beta }_1\mathrm{,}}\end{array}$ (7/a) ha viszont csúszva gördül, akkor: $\begin{array}{c}{\displaystyle S_1={\mu }_{\text{k}}{N}_1\mathrm{.}}\end{array}$ (7/b)     5. ábra 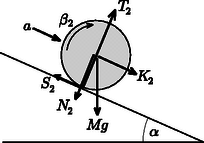      6. ábra   Az első keréknél (6. ábra) a hátsó kerékhez hasonlóan: $\begin{array}{c}{\displaystyle Ma=K_2-S_2\mathrm{,}}\end{array}$ (8) $\begin{array}{c}{\displaystyle Mg\text{cos}\alpha +N_2=T_2\mathrm{,}}\end{array}$ (9) $\begin{array}{c}{\displaystyle 0\mathrm{,}7M{R}^2{\beta }_2=S_{2}R\mathrm{.}}\end{array}$ (10) Tiszta gördülésnél $\begin{array}{c}{\displaystyle a=R{\beta }_2\mathrm{,}}\end{array}$ (11/a) ha pedig csúszva gördül, akkor: $\begin{array}{c}{\displaystyle S_2={\mu }_{\text{k}}{N}_2\mathrm{.}}\end{array}$ (11/b) 3. A különböző mozgástípusok elemzése a) Tételezzük fel, hogy olyanok a viszonyok, hogy mindkét kerék tisztán gördül. Ekkor az $\left(1\right)$‐$\left(11\right)$ egyenletrendszer tiszta gördülésre vonatkozó egyenleteinek megoldása: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle a}& {\displaystyle =\frac{5}{6}g\text{sin}\alpha \mathrm{,}{\beta }_1={\beta }_2=\frac{5}{6}\frac{g}{R}\text{sin}\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle S_1}& {\displaystyle =S_2=\frac{7}{12}Mg\text{sin}\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle K_1}& {\displaystyle =K_2=\frac{5}{12}Mg\text{sin}\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle N_1}& {\displaystyle =\left(\frac{5}{2}\text{cos}\alpha -\frac{5h}{12l}\right)Mg\mathrm{,}{N}_2=\left(\frac{5}{2}\text{cos}\alpha +\frac{5h}{12l}\right)Mg}\hfill \\ \hfill {\displaystyle T_1}& {\displaystyle =\left(\frac{7}{2}\text{cos}\alpha -\frac{5h}{12l}\right)Mg\mathrm{,}{T}_2=\left(\frac{7}{2}\text{cos}\alpha +\frac{5h}{12l}\right)Mg\mathrm{.}}\hfill \end{array}}}\end{array}$ A feltételezett tiszta gördülés akkor jön létre, ha $S_1\le {\mu }_{\text{s}}{T}_1$ és $S_2\le {\mu }_{\text{s}}{T}_2$ teljesül. Az erők behelyettesítésével látható, hogy a két feltétel közül a hátsó kerékre vonatkozó az erősebb, nevezetesen (a lejtő hajlásszögére megfogalmazva) $\begin{array}{c}{\displaystyle \text{tg}\alpha \le \frac{{\mu }_{\text{s}}}{1+\frac{5h}{7l}{\mu }_{\text{s}}}\mathrm{.}}\end{array}$ b) Ha a lejtő hajlásszöge egy kicsit meghaladja ezt a kritikus értéket, akkor a hátsó kerék csúszva, az első kerék pedig tisztán gördül. Az $\left(1\right)$‐$\left(11\right)$ egyenletrendszernek ezt az állapotot leíró egyenleteiből ‐ hosszú számolással ‐ a következőt kaphatjuk: $\begin{array}{c}{\displaystyle a=\frac{\left(1+\frac{5h{\mu }_{\text{k}}}{14l}\right)\text{sin}\alpha -\frac{1}{2}{\mu }_{\text{k}}\text{cos}\alpha }{\frac{11}{10}+\frac{5h}{11l}{\mu }_{\text{k}}}\mathrm{.}}\end{array}$ Az első kerék tiszta gördülésének feltétele: $S_2\le {\mu }_{\text{s}}{T}_2$. Ezt a feltételt a hajlásszögre kifejtve a következő adódik: $\begin{array}{c}{\displaystyle \text{tg}\alpha \le \frac{6{\mu }_{\text{s}}+77{\mu }_{\text{k}}+\frac{325h}{7l}{\mu }_{\text{s}}{\mu }_{\text{k}}}{14-\frac{5h}{l}\left({\mu }_{\text{s}}-{\mu }_{\text{k}}\right)}\mathrm{.}}\end{array}$ c) Ha a lejtő hajlásszöge ezt kritikus értéket is meghaladja, akkor mindkét kerék csúszva gördül. Az $\left(1\right)$‐$\left(11\right)$ egyenletrendszer ide vonatkozó egyenleteiből a kocsi gyorsulására és a kerekek szöggyorsulására a következő eredmény adódik: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle a}& {\displaystyle =g\left(\text{sin}\alpha -{\mu }_{\text{k}}\text{cos}\alpha \right)\mathrm{,}}\hfill \\ \hfill {\displaystyle {\beta }_1}& {\displaystyle =\frac{5}{7}\frac{g}{R}{\mu }_{\text{k}}\left(7-\frac{5h}{l}{\mu }_{\text{k}}\right)\text{cos}\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle {\beta }_2}& {\displaystyle =\frac{5}{7}\frac{g}{R}{\mu }_{\text{k}}\left(7+\frac{5h}{l}{\mu }_{\text{k}}\right)\text{cos}\alpha \mathrm{.}}\hfill \end{array}}}\end{array}$   4. A hirtelen megcsúszó jármű esete Vizsgáljuk azt az esetet, amikor az álló helyzetből induló jármű kerekei $d$ úton tisztán gördülnek, majd $s-d$ úton mozgásuk csúszva gördülés. Jelölje $a_{\text{t}}$, illetve $a_{\text{cs}}$ a jármű gyorsulását a tiszta gördülés, illetve a csúszás szakaszában, ${\beta }_{\text{<span style="font-size:10px;">első</span>}}$, illetve ${\beta }_{\text{<span style="font-size:10px;">hátsó</span>}}$ a kerekek szöggyorsulását a csúszva gördülés idején. (Ezeket a mennyiségeket a 3. részfeladatban meghatároztuk.) Az egyenletesen változó mozgásra vonatkozó kinematikai összefüggések felhasználásával könnyen kapható a jármű végsebessége, illetve az egyes kerekek szögsebessége: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle v}& {\displaystyle =\sqrt[]{2a_{\text{t}}d+2a_{\text{cs}}\left(d-s\right)}\mathrm{,}}\hfill \\ \hfill {\displaystyle {\omega }_{\text{<span style="font-size:10px;">első</span>}}}& {\displaystyle =\frac{\sqrt[]{2a_{\text{t}}d}}{R}+{\beta }_{\text{<span style="font-size:10px;">első</span>}}\frac{\sqrt[]{2a_{\text{t}}d+2a_{\text{cs}}\left(d-s\right)}-\sqrt[]{2a_{\text{t}}d}}{a_{\text{cs}}}\mathrm{,}}\hfill \\ \hfill {\displaystyle {\omega }_{\text{<span style="font-size:10px;">hátsó</span>}}}& {\displaystyle =\frac{\sqrt[]{2a_{\text{t}}d}}{R}+{\beta }_{\text{<span style="font-size:10px;">hátsó</span>}}\frac{\sqrt[]{2a_{\text{t}}d+2a_{\text{cs}}\left(d-s\right)}-\sqrt[]{2a_{\text{t}}d}}{a_{\text{cs}}}\mathrm{.}}\hfill \end{array}}}\end{array}$   Kísérleti forduló   I. feladat. Az $e/k_{\text{B}}$ arány meghatározása elektrolízissel   A rész: A kémcsövön lévő önkényes skála kalibrálása A rendelkezésre álló vékonyabb huzalból és az acélgolyóból ,,matematikai'' ingát lehetett készíteni. Ennek lengésidejét stopperrel megmérve $g$ ismeretében meg lehetett határozni az inga (centiméterben mért) hosszát, majd a huzal segítségével kalibrálni lehetett a kémcsövön lévő ‐ ismeretlen léptékű ‐ skálát.   B rész: Az $e/k_{\text{B}}$ arány meghatározása A kémcsövet szájával lefelé fordítva kellett a vízbe helyezni, elhelyezve benne az egyik elektródát. Vezetékekkel lehetett létrehozni az áramkört, amelyben mérhető volt az áramerősség. A víz alatt a vezetéket nehezékkel lehetett rögzíteni. Érdemes volt úgy megválasztani a polaritást, hogy a kémcsőben hidrogén gyűljön össze, mert ennek mennyisége éppen kétszerese a keletkező oxigén mennyiségének. Az áramerősség és az idő szorzata a töltést adja meg, ezt az elemi töltés kétszeresével leosztva megkapjuk a keletkező hidrogén molekulák számát. Az ideális gáz állapotegyenletét felírhatjuk a részecskeszám és a Boltzmann-állandó segítségével. A nyomás és a hőmérséklet pillanatnyi értékét a verseny szervezői közölték a diákokkal, akiknek így csak a térfogatváltozást kellett mérniük az előző részfeladatban kalibrált skála segítségével. A mért adatokból rövid számolás után meg lehetett határozni az $e/k_{\text{B}}$ arányt. A mérés során az egyenletes elektrolízis érdekében érdemes volt alacsony, 4 mA-nél nem nagyobb áramerősséget választani, és ezzel legalább egy órányit mérni. Ezzel a módszerrel nagyjából $10\%$-os pontossággal határozható meg az $e/k_{\text{B}}$ arány.   II. feladat. Optikai ,,fekete'' doboz   Az optikai fekete dobozban két optikai rácsot helyeztek el. Ezeket egymásra merőlegesen, vagyis keresztezett állásban, belülről felragasztották a doboz két szemközti falára. A doboz belsejében az optikai rácsokon kívül még egy megdöntött helyzetű planparalel (sík-párhuzamos) lemez is volt. A planparalel lemezre abból lehetett következtetni, hogy az optikai tengelyen haladó direkt fénysugarat az eszköz egy kissé eltérítette. Ha viszont megdöntöttük a dobozt, akkor egy bizonyos szögben történő megdöntéskor az eltérítés megszűnt. Ebből a megdöntésből lehetett megadni a planparalel lemez helyzetét a dobozban, illetve a direkt sugár eltérítéséből kaphatták meg a versenyzők a lemez vastagságát. Ehhez le kellett vezetniük az eltérítés formuláját, és ismerniük kellett az üveg törésmutatóját. A planparalel lemez adatait $20\%$-os pontossággal lehetett megkapni. A keresztezett állású optikai rácsok, valamint a dobozon lévő párhuzamos rések érdekes, meglepő hatást eredményeztek. Ha az egyik oldalról küldtük be a fényt, akkor a másik oldalon négyzetrácsszerű elhajlási képet kaptunk, ami lényegében megegyezett azzal, mintha a két rács közvetlenül érintkezne egymással. Ha viszont a doboz másik oldaláról érkezett a fény, akkor az elhajlási kép olyan volt, mintha csak egy rács lenne a dobozban, az elhajlási maximumok csak egy sorban helyezkedtek el, mégpedig a résekkel párhuzamosan. Ennek az oka az, hogy ekkor az első rács a résekre merőleges elhajlást ad, amelyek közül a második rács csak a direkt sugarat engedi érvényesülni a második résen. A rendszer ,,félvezető'', aszimmetrikus jellegét szórakoztató és egyben tanulságos is önállóan végiggondolni. Az öt magyar versenyzőből hárman jöttek rá teljes mértékben a ,,fekete doboz'' tartalmára, ami ‐ a többi ország versenyzőihez képest ‐ nagyon jó aránynak számít. Az optikai rácsok ismert elhajlási formulájából ki lehetett számítani, hogy az egyik rács rácsállandója $2\mu$m értékű, míg a másiké $1\mu$m nagyságú volt, amit $10\%$-os pontossággal lehetett meghatározni. Ebben a mérésben a versenyzőknek ‐ a kísérleti feladatoknál szinte kötelező eljárástól eltérve ‐ nem kellett hibabecsléssel foglalkozniuk. A rendezők így próbálták egy kicsit könnyebbé tenni a meglehetősen időigényes mérési feladatokat. 1A feladatok szövegét a KöMaL októberi számában közöltük.