Cím:	A 2001-2002. évi Arany Dániel Matematikai Tanulóverseny feladatai
Füzet:	2002/november, 467 - 472. oldal	PDF  |  MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. KEZDŐK Első forduló   Mindkét kategória   1. Oldja meg a következő egyenlőtlenséget a valós számok halmazán! $\begin{array}{c}{\displaystyle \frac{2x}{|x-3|-5}+\frac{1}{x+2}\ge 1}\end{array}$ (6 pont)   2. Az $ABC$ derékszögű háromszög 3 egység hosszúságú $AB$ átfogójának harmadoló pontjai $E$ és $G$. Számítsa ki a $C{E}^2+C{G}^2$ összeg pontos értékét! (6 pont)   3. Hány olyan ${10}^6$-nál kisebb természetes szám van, amely számjegyeinek összege páros és a rákövetkező természetes szám számjegyeinek összege is páros? (8 pont)   4. Egy hegyesszögű háromszögben a szokásos jelölésekkel $ac=b^2-a^2$. Bizonyítsa be, hogy $\beta =2\alpha$! (10 pont)   5. Mely $m$ és $n$ 1-nél nagyobb egész számokra teljesül, hogy $m$ osztója $n$-nek és $m^n\le n^m$? (10 pont)   Második (döntő) forduló   I. kategória: Általános tanterv szerint tanuló szakközépiskolások és gimnáziumi tanulók   1. Mi a szükséges és elégséges feltétele, hogy egy konvex $ABCD$ négyszög $AB$ és $CD$ oldalának felezőpontjai által meghatározott szakasz felezze a négyszög területét?   2. Mely $x$, $y$ és $z$ számokra teljesül az alábbi egyenlőség? $\begin{array}{c}{\displaystyle 4x^3+2y^3+z^3=2002\cdot xyz}\end{array}$   3. Mutassa meg, hogy egy kocka csúcsainak halmazából kiválasztható néhány 4-elemű részhalmaz úgy, hogy a kocka bármely három csúcsát a kiválasztott 4-elemű részhalmazok közül pontosan egy tartalmazza!   II. kategória: Speciális matematika tantervű gimnáziumi tanulók   1. Jelöljük az $ABC$ háromszög körülírt körén az $A$-t nem tartalmazó $BC$ ív felezőpontját $D$-vel! Legyen $D$ tükörképe a $BC$ egyenesre $E$, az $EA$ szakasz felezőpontja pedig $K$. Igazolja, hogy $K$ és a háromszög oldalfelező pontjai egy körön helyezkednek el!   2. Mely $x$ és $y$ egész számokra teljesül az alábbi egyenlőség? $\begin{array}{c}{\displaystyle x^2{y}^2-x^{2}y-x{y}^2+xy+x+y=2}\end{array}$   3. Legyen $n\ge 6$. Bizonyítsa be, hogy ha egy $n$ elemű halmazból kiválasztható néhány 5-elemű részhalmaz úgy, hogy az $n$ elemű halmaz minden 3-elemű részhalmazát a kiválasztott 5-elemű részhalmazok közül pontosan egy tartalmazza, akkor $n\ge 16$.   HALADÓK I. kategória: Szakközépiskolák   Első (iskolai) forduló   1. Bizonyítsuk be, hogy minden $0<a<1$ számra $\begin{array}{c}{\displaystyle \frac{{2000}^2}{1-a}+\frac{1}{a}\ge {2001}^2!}\end{array}$ Milyen $a$-ra áll fenn egyenlőség?   2. Az $ABC$ háromszög $AB$ oldalának $B$-hez közelebbi harmadolópontja $H$, a $BC$ oldal $B$-hez legközelebbi negyedelőpontja $N_1$, $C$-hez legközelebbi negyedelőpontja $N_2$. A $CA$ oldal felezőpontja $F$. Bizonyítsa be, hogy az $FH{N}_1$ és az $FH{N}_2$ háromszögek területének összege az $ABC$ háromszög területének felével egyenlő!   3. Oldjuk meg a valós számok halmazán az $\begin{array}{c}{\displaystyle {\left(x^2+y^2\right)}^3={\left(x^3-y^3\right)}^2}\end{array}$ egyenletet!   4. Bizonyítsuk be, hogy $2001$ egymást követő pozitív egész szám között mindig van olyan, amelyre igaz, hogy a számjegyeinek összege osztható $27$-tel!   5. Egy $20\times 25$-ös téglalapban elhelyeztünk tetszőlegesen $120$ db egységnyi oldalú négyzetet. Bizonyítsuk be, hogy még egy olyan egységnyi átmérőjű kör is elfér a téglalapban, amelynek nincs közös belső pontja a négyzetekkel! (Négyzeten most négyzetlapot, körön pedig körlapot értünk.)   Második forduló   1. Bizonyítsuk be, hogy $\begin{array}{c}{\displaystyle 1\cdot 2\cdot \text{...}\cdot 2001+2002\cdot 2003\cdot \text{...}\cdot 4002}\end{array}$ osztható $4003$-mal!   2. Oldjuk meg a természetes számok halmazán a $\sqrt[]{x+y}+\sqrt[]{x-y}=10$ egyenletet!   3. Az $a$ és $b$ befogójú derékszögű háromszög átfogóhoz tartozó magassága az átfogó negyedrésze. Mekkora ekkor ${\left(\frac{a}{b}\right)}^6+{\left(\frac{b}{a}\right)}^6$ értéke?   4. Egy $1$ egység széles egyenes vonalzóval egy síkon szerkeszthetünk. Más segédeszközünk ‐ ceruzán kívül ‐ nincs. A szerkesztés során a következő lépések hajthatók végre: $a)$ tetszőleges számú pontot felvehetünk az adott síkon, $b)$ két felvett ponton át egyenes húzható a vonalzóval, $c)$ bármely megrajzolt egyenessel attól egységnyi távolságra lévő párhuzamos egyenes húzható. Szerkesszünk $\sqrt[]{34}$ egység hosszú szakaszt a megengedett szerkesztési lépések alapján!   Harmadik (döntő) forduló   1. Az $a$, $b$, $c$, $d$ egész számokra $a<b<c<d$ teljesül. Tudjuk, hogy az $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle E}& \hfill {\displaystyle =}\hfill & {\displaystyle \left(b-a\right)\left(b+c+d\right)\left(c+a+d\right)+\left(c-b\right)\left(c+a+d\right)\left(a+b+d\right)+}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle +\left(a-c\right)\left(a+b+d\right)\left(b+c+d\right)}\hfill \end{array}}}\end{array}$ kifejezés értéke prímszám. Mi ennek a prímszámnak az értéke?   2. Az $ABC$ derékszögű háromszög $BC$ befogójának $D$ pontjában az $AD$ szakaszra állított merőleges az $AB$ átfogót az $E$ pontban metszi. Az $E$ pont $BC$-re eső merőleges vetülete az $F$ pont. Bizonyítsuk be, hogy a $CF$ szakasz hossza akkor minimális, ha a $D$ pont rajta van az $A$ csúcsból induló szögfelezőn.   3. $a)$ Bizonyítsuk be, hogy végtelen sok olyan $k$ egész szám van, amelyre $k$ és $k+1$ is két pozitív egész szám négyzetének összegeként írható fel. $b)$ Igazoljuk azt is, hogy nem létezik olyan $k$ egész szám, amelyre a $k$, $k+1$, $k+2$ és $k+3$ számok mindegyike felbontható két négyzetszám összegére.   II. kategória: Általános matematika tantervű gimnáziumok   Első (iskolai) forduló   1. Bizonyítsuk be, hogy ha az $x$ és $y$ valós számokra igaz, hogy $x+y+xy$ racionális szám, $x^4+y^4$ pedig irracionális szám, akkor $xy$ csak irracionális szám lehet.   2. Az $O$ középpontú egységnyi sugarú körbe írt $ABCD$ trapézban $BOC\sphericalangle =AOD\sphericalangle ={120}^{\circ }$, ahol $BC$ és $AD$ a trapéz szárai. Mutassuk meg, hogy a trapéz területe legfeljebb $\sqrt[]{3}$ területegység értékű!   3. Adott a valós számok halmazán értelmezett $x\mapsto x^2-4|x-1|-p$ függvény, ahol $p$ valós paraméter. Határozzuk meg $p$ értékét úgy, hogy $x$-nek pontosan $3$ különböző értékére legyen az adott függvény értéke $1$.   4. Bizonyítsuk be, hogy $2001$ egymást követő pozitív egész szám között mindig van olyan, amelyre igaz, hogy a számjegyeinek összege osztható $27$-tel!   5. Egy $20\times 25$-ös téglalapban elhelyeztünk tetszőlegesen $120$ db egységnyi oldalú négyzetet. Bizonyítsuk be, hogy még egy olyan egységnyi átmérőjű kör is elfér a téglalapban, amelynek nincs közös belső pontja a négyzetekkel! (Négyzeten most négyzetlapot, körön pedig körlapot értünk.)   Második forduló   1. Oldjuk meg az egész számok körében az $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle ab+cd}& {\displaystyle =-1}\hfill \\ \hfill {\displaystyle ac+bd}& {\displaystyle =-1}\hfill \\ \hfill {\displaystyle ad+bc}& {\displaystyle =-1}\hfill \end{array}}}\end{array}$ egyenletrendszert!   2. Az $a$ és $b$ befogójú derékszögű háromszög átfogóhoz tartozó magassága az átfogó negyedrésze. Mekkora ekkor ${\left(\frac{a}{b}\right)}^6+{\left(\frac{b}{a}\right)}^6$ értéke?   3. Bizonyítsuk be, hogy ha az $a$, $b$, $c$ valós számokra teljesül az $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}$ összefüggés, akkor $\begin{array}{c}{\displaystyle \frac{1}{a^{1001}}+\frac{1}{b^{1001}}+\frac{1}{c^{1001}}=\frac{1}{a^{1001}+b^{1001}+c^{1001}}\mathrm{.}}\end{array}$   4. Az $ABCD$ konvex négyszög $AC$ és $BD$ átlója merőleges egymásra. Az $AB$ oldal $K$ felezőpontjából állítsunk merőlegest $DC$ oldalegyenesre. Ennek talppontja legyen $P$. Az $AD$ oldal $L$ felezőpontjából a $BC$ oldalegyenesre állított merőleges talppontja legyen $Q$. Bizonyítsuk be, hogy a $KP$ és $LQ$ egyenesek az $AC$ átló egyenesén metszik egymást!   Harmadik (döntő) forduló   1. Hány olyan pozitív egész tízes számrendszerbeli $n$-jegyű szám van, amelynek számjegyösszege $n^3-40$, ahol $n$ pozitív egész szám?   2. Az $ABC$ háromszögben $BC<CA<AB$. A $BC$ oldal felező merőlegese a $P$, az $AC$ oldal felező merőlegese a $Q$ pontban metszi a $C$ csúcsból induló magasság egyenesét. Mekkora a háromszög legnagyobb szöge, ha $4CP\cdot CQ=A{B}^2$?   3. Tekintsük az $\mathrm{1,2,3,}\text{...}\mathrm{,2002}$ számsorozatot! Ezt a sorozatot átrendezhetjük a következő módon: egy lépésben a sorozat utolsó tagját előbbre helyezhetjük (akárhányadik helyre az $\mathrm{1.,2.,3.,}\text{...}\mathrm{,2002.}$ sorszámú hely közül) azzal a megszorítással, hogy az előrébb helyezett tag nem előzhet meg nála nagyobb számot. A kapott új sorozatra ismét alkalmazható az előbb leírt lépés, egészen addig, amíg lehetséges. Bizonyítsuk be, hogy bármely lépés után olyan sorozatot kapunk, amelyben a $\left(2k-1\right)$-edik és a $2k$-adik tag közül az egyik páros, a másik pedig páratlan szám, bármely $1\le k\le 1001$ esetén.   III. kategória: Speciális matematika tantervű gimnáziumok   Első (iskolai) forduló   1. Bizonyítsuk be, hogy ha az $a$, $b$, $c$ valós számokra teljesül az $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}$ összefüggés, akkor $\begin{array}{c}{\displaystyle \frac{1}{a^{1001}}+\frac{1}{b^{1001}}+\frac{1}{c^{1001}}=\frac{1}{a^{1001}+b^{1001}+c^{1001}}\mathrm{.}}\end{array}$   2. Az $a$ oldalú $N$ négyzetet a középpontja körül elforgatva az $N\text{'}$ négyzetet kapjuk. A két négyzet közös része olyan nyolcszög, amelynek mindegyik oldala $b$ hosszú. $a)$ Fejezzük ki a nyolcszög területét $a$-val és $b$-vel! $b)$ Ha az $N$ és $N\text{'}$ négyzet metszetének területe $t$, uniójának területe pedig $T$, akkor igazoljuk, hogy $\sqrt[]{t\cdot T}<a^2<\sqrt[]{\frac{t^2+T^2}{2}}$. 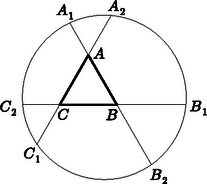3. A $k$ kör belsejében levő $ABC$ szabályos háromszög oldalegyenesei a $k$ kört az $A_1$, $A_2$, $B_1$, $B_2$, $C_1$, $C_2$ pontokban metszik a következő betűzés szerint: az $AB$ oldalegyenes metszéspontjai a körrel $A_1$ és $B_2$. Hasonlóan: a $BC$ egyenes metszetei a körrel $B_1$, illetve $C_2$, és a $CA$ egyenes metszetei a körrel $C_1$, illetve $A_2$ az ábrának megfelelően.     Bizonyítsuk be, hogy $\begin{array}{c}{\displaystyle A{A}_1+B{B}_1+C{C}_1=A{A}_2+B{B}_2+C{C}_2\mathrm{.}}\end{array}$   4. $121$ darab pozitív egész számról tudjuk, hogy összegük $360$. Bizonyítsuk be, hogy az adott $121$ darab pozitív egész szám közül ki lehet néhányat választani úgy, hogy a kiválasztott számok összege $120$ legyen.   Második (döntő) forduló   1. Bizonyítsuk be, hogy az összes olyan pozitív egész alapú számrendszerben, amelyben az $\overline{abc}$ és a $\overline{cba}$ pozitív egész szám hányadosa 2, teljesül az $a+c=b$ összefüggés.   2. Adott egy $2k+1$ oldalú szabályos sokszög, melynek belsejében vagy határán felveszünk egy $P$ pontot. $P$-nek a sokszög csúcsaitól mért távolságát jelölje (nagyság szerinti sorrendben) $d_1\le d_2\le \text{...}\le 2_{2k+1}$. Milyen $P$ pont esetén lesz $d_{k+1}$ maximális?   3. Van $N$ darab chip, amelyek képesek egymás tesztelésére a következő módon: ha kettőt összekapcsolunk, akkor mindkettő kijelzi a másik chipről, hogy jó-e vagy hibás. A jó chip mindig helyesen válaszol, a hibás chip véletlenszerű eredményt ad. Tudjuk, hogy az összes chipnek több mint a fele jó. Lehetséges-e $N$-nél kevesebb teszt végrehajtásával kiválasztani egy jó chipet?