Kezdőlap


Cím:	Mathematica
Szerző(k):	Lóczi Lajos
Füzet:	2002/szeptember, 351 - 357. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Idén, 2002-ben ünnepli 14. születésnapját a Mathematica. E kezdetben Stephen Wolfram nevéhez fűződő számítógépes matematikai programot az évek során kiváló szakemberek tucatjai fejlesztették tovább (jelenleg a 4.1-es verziónál tartunk), s mára a legbonyolultabb számítógépes rendszerek között tartják számon. Felhasználói tábora meghaladja az egymilliót és szinte minden tudományterület képviselői megtalálhatók közöttük. Sokoldalúságának és teljesítményének köszönhetően a kutatásban és az iparban egyaránt használják. Kétszáznál több könyv és tucatnyi Mathematica-hoz (sőt, magában Mathematica-ban) írt programcsomag, alkalmazás látott napvilágot.
Mindez annak tudható be, hogy a Mathematica éppúgy alkalmas nagypontosságú számítások gyors elvégzésére, mint szimbolikus (pl. algebrai) kifejezések és objektumok kezelésére. A legkülönfélébb két- és háromdimenziós ábrák, grafikonok készíthetők segítségével. A Mathematica egyben logikusan átgondolt és felépített programnyelv is: rugalmassága éppen abban rejlik, hogy a sok száz beépített matematikai függvényt, illetve utasítást szabadon ötvözhetjük a saját magunk által megírottakkal.
A Mathematica-ról e jelen bevezetőnél bővebb ismertetőt tartalmaz az [1] cikk. Részletes magyar nyelvű útmutató a program használatáról a [2] könyv. Wolfram [3] könyve teljességre törekszik. Elmélyülve a Wolfram Research [4] honlapján, rengeteg érdekes információra lelhetünk. Szintén ők működtek közre az [5] (folyamatosan bővülő) internetes matematikai enciklopédia elkészítésében. Egy új kezdeményezés, a webMathematica segítségével a böngészőprogramok által internetről futtatható Mathematica-alkalmazások hozhatók létre. Ezzel kapcsolatban a [6] és [7] webcímre utalunk.
Kedvcsinálóul néhány (önkényesen, s semmiképpen sem szisztematikusan választott) feladatot oldunk meg a Mathematica segítségével. A feladatok rövidek és inkább csak illusztratív jellegűek, összetettebb problémák részekre bontásakor azonban sok-sok ehhez hasonlóval találkozhatunk. A megoldásokhoz rövid magyarázatot fűzünk, ezekkel igyekszünk megvilágítani egy-egy parancs működését. Az általunk begépelendő parancsokat írógépbetű-típussal emeltük ki.

Példák

1. Hozzuk egyszerűbb alakra a

\begin{matrix} (\sqrt[]{2 + \sqrt[]{3}} + \sqrt[]{2 - \sqrt[]{3}}) (\sqrt[]{5 + \sqrt[]{21}} - \sqrt[]{5 - \sqrt[]{21}}) \end{matrix}

kifejezést.

A Mathematica fő egyszerűsítő parancsát

\begin{matrix} FullSimplify[(\sqrt[]{2 + \sqrt[]{3}} + \sqrt[]{2 - \sqrt[]{3}}) (\sqrt[]{5 + \sqrt[]{21}} - \sqrt[]{5 - \sqrt[]{21}})] \end{matrix}

használva eredményül

6

adódik. Figyeljük meg, hogy a Mathematica különbséget tesz a kis- és nagybetűk között. A beépített parancsnevek nagy kezdőbetűvel írandók. Függvény- és parancsargumentumok megadásakor szögletes zárójelet kell használnunk.

2. Írjuk fel a

cos 4 x + sin 5 x

kifejezést az egyszeres szögek szögfüggvényei segítségével.

A TrigExpand[Cos[4 x]+Sin[5 x]] utasítás eredményeként

\begin{matrix} Cos {[x]}^{4} + 5 Cos {[x]}^{4} Sin [x] - 6 Cos {[x]}^{2} Sin {[x]}^{2} - 10 Cos {[x]}^{2} Sin {[x]}^{3} + Sin {[x]}^{4} + Sin {[x]}^{5} \end{matrix}

adódik.

3. Bontsuk szorzattá az előbbi kifejezést.

A TrigFactor[%] parancs hatására ezt kapjuk (a % jel az előző eredményt jelenti):

\begin{matrix} - {(Cos [\frac{x}{2}] + Sin [\frac{x}{2}])}^{2} (- 1 + 2 Sin [x]) (1 + 2 Sin [3 x]) \end{matrix}

(Melyik utasítással nyerhető vissza ebből az eredeti

cos 4 x + sin 5 x

alak?)

4. Adjuk meg

cos 3^{\circ}

pontos értékét.

A Mathematica FullSimplify[FunctionExpand[Cos[3 Degree]]] utasítása az alábbi legegyszerűbb alakot adja meg:

\begin{matrix} \frac{1}{2} \cdot \sqrt[]{\frac{1}{2} (4 + \sqrt[]{7 + \sqrt[]{5} + \sqrt[]{6 (5 + \sqrt[]{5})}})} \end{matrix}

5. Alakítsuk szorzattá az

x^{15} - 1

polinomot.

A Factor[x

^{15}

-1] utasítás 4 tényezőre bontja polinomunkat:

\begin{matrix} (- 1 + x) (1 + x + x^{2}) (1 + x + x^{2} + x^{3} + x^{4}) (1 - x + x^{3} - x^{4} + x^{5} - x^{7} + x^{8}) \end{matrix}

Ebben a felbontásban minden együttható racionális szám. Ha a racionális számtestet a

\sqrt[]{5}

elemmel bővítjük,

\begin{matrix} Factor[x^{15} -1,Extension \to \sqrt[]{5}] \end{matrix}

a polinom tovább bontható:

\begin{matrix} \begin{matrix} \frac{1}{16} (- 1 + x) (- 2 - x + \sqrt[]{5} x - 2 x^{2}) (1 + x + x^{2}) (2 + x + \sqrt[]{5} x + 2 x^{2}) \cdot \\ \cdot (- 2 + x + \sqrt[]{5} x - x^{2} - \sqrt[]{5} x^{2} + x^{3} + \sqrt[]{5} x^{3} - 2 x^{4}) \cdot \\ \cdot (2 - x + \sqrt[]{5} x + x^{2} - \sqrt[]{5} x^{2} - x^{3} + \sqrt[]{5} x^{3} + 2 x^{4}) . \end{matrix} \end{matrix}

6. Adjuk meg a

2^{67} - 1

szám prímtényezős felbontását.

A FactorInteger[2

^{67}

-1] parancs ezt adja:

\begin{matrix} {{193707721,1}, {761838257287,1}} \end{matrix}

azaz

2^{67} - 1

felírható, mint két óriási prímszám (nevezetesen

193 707 721

és

761 838 257 287

) első hatványának szorzata.

7. Oldjuk meg az

x + y + z = 2

x y + x z + y z = - 5

x y z = - 6

egyenletrendszert.

Ezt a Mathematica-ban így tehetjük meg:

\begin{matrix} Solve[x+y+z==2 && x y+x z+y z==-5 && x y z==-6] \end{matrix}

A Mathematica a dupla egyenlőségjellel vizsgálja két kifejezés egyenlőségét, a szimpla egyenlőségjel változó értékének definiálására szolgál. A && jel jelenti a logikai és műveletét. A változóneveket nem írhatjuk egybe, a szóköz jelenti a szorzást. Megoldásként egy listában a változók mind a hat lehetséges sorrendjét megkapjuk:

\begin{matrix} \begin{matrix} {{x \to - 2, y \to 1, z \to 3}, {x \to - 2, y \to 3, z \to 1}, {x \to 1, y \to - 2, z \to 3}, \\ {x \to 1, y \to 3, z \to - 2}, {x \to 3, y \to - 2, z \to 1}, {x \to 3, y \to 1, z \to - 2}} \end{matrix} \end{matrix}

8. Oldjuk meg az

a x^{2} + b x + c = 0

egyenletet, ahol

a

b

c

tetszőleges számok.

A Reduce[a x

^{2}

+b x+c==0,x] parancs eredménye:

\begin{matrix} \begin{matrix} x = = \frac{- b - \sqrt[]{b^{2} - 4 a c}}{2 a} & & a \neq 0 | | x = = \frac{- b + \sqrt[]{b^{2} - 4 a c}}{2 a} & & a \neq 0 | | \\ a = = 0 & & b = = 0 & & c = = 0 | | a = = 0 & & x = = - \frac{c}{b} & & b \neq 0 \end{matrix} \end{matrix}

A Reduce parancsot használtuk, amely paramétert is tartalmazó egyenlet általános megoldását adja meg. A Solve utasítás csak az ún. generikus megoldásokat adná meg, jelen esetben csak a másodfokú egyenlet megoldóképletét, ami az

a = 0

esetben nem lenne megfelelő. A

| |

jel jelenti a logikai megengedő vagy műveletét. (Ennek prioritása alacsonyabb az és (

& &

) műveleténél, ezért nem szükségesek zárójelek). A fenti eredmény értelmezése tehát: ha

a \neq 0

, akkor

x

egyenlő a másodfokú egyenlet két megoldásával; ha

a = 0

, de

b \neq 0

, akkor az elsőfokú egyenlet megoldóképletét kapjuk vissza; végül, ha

a = b = c = 0

, akkor

x

-re nincs megkötés.

9. Tudjuk, hogy

a + b + c = 1

a^{2} + b^{2} + c^{2} = 2

és

a^{3} + b^{3} + c^{3} = 3

. Mennyivel egyenlő ekkor

a^{5} + b^{5} + c^{5}

\begin{matrix} \begin{matrix} Eliminate[ & {mennyi==a^{5} +b^{5} +c^{5}, a+b+c==1, a^{2} +b^{2} +c^{2} ==2, a^{3} +b^{3} +c^{3} ==3}, \\ {a,b,c}] \end{matrix} \end{matrix}

Erre ezt kapjuk:

\begin{matrix} mennyi = = 6 \end{matrix}

Az Eliminate utasítás ugyanis kiküszöböli a felsorolt egyenletekből a megadott változókat (jelen esetben

a

b

c

-t). Ami megmarad, éppen az ötödik hatványösszeg. (Hogyan oldható meg a feladat általánosabban: a jobb oldalakon álló 1, 2, 3 számok helyett

α

β

γ

paraméterekkel?)

10. Határozzuk meg

{(a + b + c + d)}^{17}

-ben

a^{3} b^{13} d

együtthatóját.

Egy lehetséges megoldást ad az alábbi utasítás:

\begin{matrix} Coefficient[Expand[(a+b+c+d)^{17}], a^{3} b^{13} d] \end{matrix}

A kifejezést az Expand bontja ki. Az eredmény

9520

11. Igazoljuk, hogy

{(\sum_{k = 1}^{n} k)}^{2} = \sum_{k = 1}^{n} k^{3}

, tetszőleges

n \geq 1

természetes szám esetén.

Az állítást a

\begin{matrix} Sum[k, {k, 1, n}]^{2} == Sum[k^{3}, {k, 1, n}] \end{matrix}

parancs eredményeként adódó True (azonosan igaz logikai érték) bizonyítja. (Természetesen a Mathematica-val külön-külön kiszámolva a két oldalt

(\frac{1}{4} n^{2} {(1 + n)}^{2})

magunk is megállapíthatjuk azok egyenlőségét.)

12. Oldjuk meg az

| | x - 1 | - 1 | + | | x | - 4 | < 3

egyenlőtlenséget.

Ehhez először betöltjük az < <Algebra`InequalitySolve` csomagot. Ezután az

\begin{matrix} InequalitySolve[Abs[Abs[x-1]-1]+Abs[Abs[x]-4]<3, x] \end{matrix}

parancs adja meg a megoldást:

\frac{3}{2} < x < \frac{9}{2}

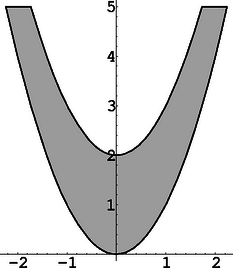
13. Határozzuk meg a

0 \leq y - x^{2} \leq 2

és a

- 5 \leq x \leq 5

0 \leq y \leq 5

egyenlőtlenségekkel határolt síkbeli tartomány területét.

A tartomány speciális alakja miatt olvassuk be a < <Calculus`Integration` csomagot. Ezután a keresett terület a következő határozott integrállal számolható ki:

\begin{matrix} Integrate[Boole[0 \leq y-x^{2} \leq 2], {x, -5, 5}, {y, 0, 5}] \end{matrix}

Az eredmény

- 4 \sqrt[]{3} + \frac{20 \sqrt[]{5}}{3}

lesz.
Magát a tartományt egyébként a < <Graphics`InequalityGraphics` csomag beolvasása után az InequalityPlot[0

\leq

y-x

^{2} \leq

2, {x, -5, 5}, {y, 0, 5}] utasítás rajzolja ki.

1. ábra

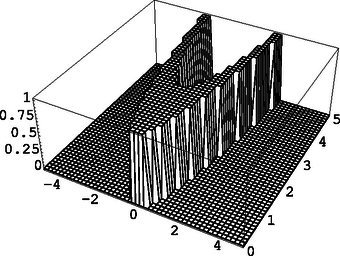
A Boole logikai függvény értéke ott 1, ahol a megadott egyenlőtlenség fennáll, másutt zérus. Ez a Plot3D[Boole[0

\leq

y-x

^{2} \leq

2], {x, -5, 5}, {y, 0, 5}] paranccsal szemléltethető.

2. ábra

14. Hozzuk egyszerűbb alakra a ,,(ha A, akkor B) és (A vagy B)'' logikai állítást.

A LogicalExpand[Implies[A, B] && (A || B)] parancs eredménye értelmében a fenti állítás logikailag egyenértékű a

B

állítással.

15. Adjuk meg azon pozitív egészeket, melyek egyszerre

n^{4} + n^{2}

és

k^{3} + 1

alakúak, alkalmas

1 \leq n \leq 10^{4}

1 \leq k \leq 10^{4}

pozitív egészekkel.

Az alábbi parancs

\begin{matrix} Intersection[Table[n^{4} +n^{2}, {n, 1, 10000}], Table[k^{3} +1, {k, 1, 10000}]] \end{matrix}

két megoldást szolgáltat:

\begin{matrix} {2,1332} \end{matrix}

(Ellenőrzés:

1^{4} + 1^{2} = 2 = 1^{3} + 1

, illetve

6^{4} + 6^{2} = 1332 = 11^{3} + 1

.) A megoldás során két, a kívánt alakú számokból álló listát hozunk létre, majd vesszük ezen listák (vagy ha tetszik, halmazok) metszetét. Tudnánk még ilyen tulajdonságú számokat találni?

16.

1

és

10000

között

4 k + 1

vagy

4 k + 3

alakú prímből van több?

4 k + 1

alakú,

10000

-nél kisebb prímek száma

609

, míg a

4 k + 3

alakúaké

619

, amint ezt az alábbi parancsok kiszámolják:

\begin{matrix} \begin{matrix} Length[Select[Range[10000]], (PrimeQ[#] && Mod[#,4]==1)&] \\ Length[Select[Range[10000]], (PrimeQ[#] && Mod[#,4]==3)&] \end{matrix} \end{matrix}

Vegyük szemügyre például az első sort. A Select parancs egy listába gyűjti ki azokat az elemeket a Range[10000] által létrehozott

{1,2, ...,10000}

listából, melyeket # helyébe helyettesítve a

\begin{matrix} ,,(prím-e #) és (4-gyel maradékosan osztva 1-et ad-e maradékul #)'' \end{matrix}

nyitott mondatban igaz értéket kapunk. (Az ilyen nyitott mondatot vagy függvényt a Mathematica-ban tiszta függvénynek nevezzük. A tiszta függvényt & jellel kell lezárnunk.) Végül a Length megszámolja, hány elemet tartalmaz e kiválogatott lista.

17. Előfordul-e valahol a

π

szám tizedestört alakjában az

1234

szám?

Erre a kérdésre számítógép nélkül aligha válaszolhatnánk. A Mathematica-val a megoldás elegáns: az

1234

sorozat már az első

15 000

jegy között előfordul, mert a

\begin{matrix} StringMatchQ[ToString[N[π, 15000]], "*1234*"] \end{matrix}

parancs True, azaz igaz értéket ad. Az N függvénnyel először meghatároztuk

π

értékét

15 000

jegy pontossággal, ezt karakterlánccá alakítottuk át, majd megnéztük, ez tartalmazza-e valahol az "1234" jelsorozatot. Azt is meg tudjuk mondani, hogy pontosan hol: a

\begin{matrix} StringPosition[ToString[N[π, 15000]], "1234"] \end{matrix}

utasítás eredménye

{{13809, 13812}}

, tehát

π

jegyei között az "1234" szám a tizedesvessző után először a

13 807

‐

13 810

. helyen fordul elő. (Figyelembe vettük ugyanis, hogy a karakterlánccá alakított

π

-jegyek első két tagja a 3-as és maga a tizedespont.) Meg tudnánk-e oldani a feladatot úgy is, hogy nem alakítjuk át a tizedesjegyeket karakterlánccá?

18. Hány nullára végződik 1000 faktoriálisa?

E jól ismert kérdésre két megoldást is adunk, a válasz egyébként 249. Az első megoldás egy ciklus segítségével számol:

\begin{matrix} a=1000!;n=0;While[\frac{a}{10} \in Integers, n++; a= \frac{a}{10}];n \end{matrix}

Az értékadások után addig osztjuk az

1000!

számot 10-zel, amíg csak egész az eredmény. Minden egyes osztáskor eggyel növeljük

n

értékét, így a nullák számát az

n

változó tartalmazza a ciklus végén, amit ki is íratunk. (A pontosvessző teszi lehetővé, hogy több utasítást írjunk egymás után egy sorba.)
Második megoldásunk általánosabb. Egy

f

függvényt definiálunk, mely tetszőleges, 4-nél nagyobb egész számot elfogad bemenetként, majd megadja, hogy hány nullára végződik

n

faktoriálisa:

\begin{matrix} f[n_Integer/;n>4] := Length[Split[IntegerDigits[n!]][[-1]]] \end{matrix}

Először

n!

számjegyeit az IntegerDigits segítségével egyesével egy listába tesszük. E listát a Split olyan részlistákra bontja, melyek az eredeti lista egymás után álló azonos elemeiből állnak. Ennek vesszük utolsó elemét a [[-1]] utasítással (az

n > 4

feltétel garantálja, hogy valóban nullák állnak hátul), majd meghatározzuk az így adódó lista hosszát. (Például a Split[IntegerDigits[10!]] eredménye a

{{3}, {6}, {2}, {8,8}, {0,0}}

lista, melynek utolsó eleme

{0,0}

.) f[1000] eredménye természetesen ezzel a módszerrel is 249.

19. Írjunk függvényt egy szám faktoriálisának kiszámítására.

A számtalan lehetőség közül egy hatékony megoldást szolgáltat az alábbi definíció:

\begin{matrix} faktorialis[n_/; n \in Integers && n \geq 1] := Apply[Times, Range[n]] \end{matrix}

Hogy megvilágítsuk a definíció jobb oldalának működését, tekintsük az

n = 3

esetet. Ekkor Range[3] értéke az

{1,2,3}

lista (melyet a Mathematica List[1,2,3] alakban tárol). Ennek fejét, azaz a List szót az Apply parancs Times-ra, azaz a szorzásra cseréli. Viszont Times[1,2,3] eredménye

1 \cdot 2 \cdot 3

, azaz 6.

20. Írjuk meg a komplexgyokrajzolo függvényt, melynek bemenete egy egyváltozós polinom, eredménye pedig e polinom gyökeinek képe a komplex számsíkon.

A Mathematica-ban mindez egyetlen összetett utasításként megvalósítható:

\begin{matrix} \begin{matrix} komplexgyokrajzolo[polinom_] := \\ ListPlot[Cases[NSolve[polinom==0][[All, 1, 2]], \\ z:(_Complex|_Real) \to {Re[z], Im[z]}], PlotStyle \to PointSize[0.03]] \end{matrix} \end{matrix}

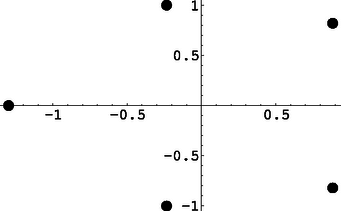
A nullára rendezett egyenletet először numerikusan megoldjuk (NSolve). Az eredmény egy (általában) komplex számokat tartalmazó speciális szerkezetű lista. A komplex számok közvetlenül még nem ábrázolhatók. Ezért e számokat rendre kigyűjtjük (erre szolgál az [[All, 1, 2]] operátor), majd (a valós-képzetes résznek megfelelően) valós koordináta-párokká alakítjuk, és egy új listában helyezzük el őket (ezt a Cases teszi meg). Végül ábrázoljuk ezt az új listát (ListPlot). (Mivel a Mathematica által választott pontméretet kicsinek találtuk, a PointSize segítségével megnöveltük a pontok méretét). Mindez az

x^{5} + x^{2} + 2

polinomra alkalmazva a 3. ábrán látható módon fest.

3. ábra

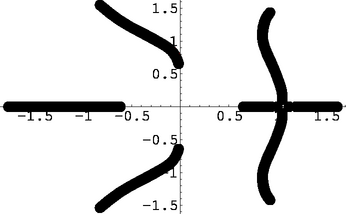
Végül az

x^{5} + n x^{2} + 2

egyenlet gyökeit ábrázoltuk, amint

n

(- 5)

-től

5

-ig fut,

\frac{1}{10}

-es lépésekben (4. ábra).

4. ábra

Hivatkozások

[1] Lóczi Lajos: A Mathematica első évtizede, Természet Világa, 129. évf. 11. sz. (1998) 515‐518. oldal
[2] Szili László ‐ Tóth János: Matematika és Mathematica, ELTE Eötvös Kiadó, Budapest, 1996.
[3] Stephen Wolfram: The Mathematica Book, 4th edition, Wolfram Media/Cambridge University Press, 1999.
[4] www.wolfram.com
[5] mathworld.wolfram.com
[6] www.integrals.com
[7] www.wolfram.com/products/webmathematica/examples