Cím: A háromszögek súlypontjáról
Szerző(k):  Légrádi Imre 
Füzet: 2002/május, 299 - 302. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A háromszögeket fizikai értelemben (a tömegeloszlásuk különbözősége alapján) három csoportra oszthatjuk. Nulldimenziós háromszögnek nevezhetjük azokat, amelyeket három ‐ nem egy egyenesbe eső ‐ pontszerű, véges tömeggel rendelkező test jelöl ki. Az egydimenziós háromszöget három vékony, de tömeggel rendelkező (homogén tömegeloszlású) rúd alkotja. Végül kétdimenziós háromszögnek a vékony, de tömeggel rendelkező, (homogén tömegeloszlású) háromszög alakú lemezt nevezhetjük. Bármelyik típusú háromszöget tekintjük is, ha az a Föld felszínén helyezkedik el és a mérete a Föld sugarához képest kicsi, akkor a súlypontja azonosnak tekinthető a tömegközéppontjával.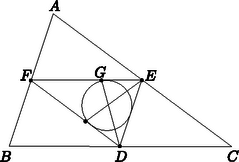
A geometriában egy háromszög súlypontja minden esetben a három súlyvonalának metszéspontja. Fizikai értelemben a súlypont már nem ilyen egyértelmű: helye függ attól, hogy hány ,,dimenziós'' háromszögről van szó.
A nulldimenziós háromszög súlypontjának helye úgy határozható meg, hogy először két tömegpont súlypontját keressük meg (ez a két pontot összekötő egyenest a tömegekkel fordított arányban osztja két részre); ezután ebbe a pontba képzelve a két pont tömegének összegét képviselő új pontot, ennek és a harmadik pontnak a közös súlypontját határozzuk meg. Ilyen esetben ‐ a tömegek nagyságától függően ‐ a háromszög fizikai súlypontja bárhova kerülhet azon a területen belül, amelyet a három tömegpont mint geometriai háromszög határoz meg. A fizikai súlypont csak akkor esik egybe a három pont által meghatározott háromszög geometriai súlypontjával, ha a három pont tömege egyenlő.
Hasonlóan egyszerű a kétdimenziós háromszög, vagyis a háromszög alakú (homogén) lap súlypontjának meghatározása. Az eljárás (a háromszöglapnak gondolatban vékony csíkokra való vagdosása) megtalálható például a közkedvelt ,,Holics Fizikában'' is, az I. kötet 2.2.3.2. pontjában, ezért itt nem foglalkozunk vele. A súlypont fizikai helyéül ez esetben is visszakapjuk a geometriai háromszög súlyvonalainak metszéspontját, vagyis a háromszög geometriai súlypontját.
Nem ilyen egyszerű azonban a vékony lécekből alkotott egydimenziós háromszög fizikai súlypontjának meghatározása. Minthogy a fizikában, a fizikai gyakorló- és versenyfeladatokban gyakran előfordul a vékony rudakból, lécekből vagy huzalokból készített háromszög (lásd pl. a 2000/2001. tanévi OKTV I. fordulóját), a következőkben ezt a problémát vizsgáljuk meg.

 
 

1. ábra
 

Tekintsünk egy egyenletes keresztmetszetű, homogén tömegeloszlású, azonos sűrűségű vékony rudakból álló háromszöget. Az oldalak hossza ‐ az 1. ábra jelöléseivel ‐ legyen BC=a, CA=b és AB=c (a≥b≥c). A tömegközéppont megkeresését a nulldimenziós háromszög esetére vezetjük vissza. Az egyes oldalak (rudak) tömegközéppontja a felezőpontjukban van, a hozzájuk rendelt tömeg pedig az oldal hosszúságával arányos. Ennek megfelelően a D pontba k⋅a, az E pontba k⋅b, az F pontba pedig k⋅c nagyságú tömeget képzelhetünk, ezen három tömegpont tömegközéppontja ugyanott van, mint az eredeti egydimenziós háromszögé. Az E pontbeli és az F pontbeli tömegek tömegközéppontja, a G pont az EF szakaszt a tömegekkel fordított arányban osztja, vagyis
GFGE=k⋅bk⋅c.
Ennek az aránypárnak a jobb oldalát írhatjuk b2:c2 alakban is, ami azt jelenti, hogy G az EF oldalt olyan arányban osztja ketté, ahogyan a DEF háromszög DF oldalának hossza aránylik DE oldalának hosszához. Ez nem más, mint a szögfelező-tételben szereplő arány; a DG egyenes tehát a DEF háromszög D csúcsára illeszkedő belső szög szögfelezője.
A nulldimenziós DEF háromszög tömegközéppontja tehát ezen a DG szögfelezőn található. Minthogy a nulldimenziós háromszög tömegközéppontjának megkeresését kezdhettük volna például a D és F pontokba képzelt k⋅a, illetve k⋅c tömegek közös tömegközéppontjának meghatározásával is, és kaptuk volna, hogy az a DF oldalt a2:c2 arányban osztja, azaz rajta volna a DEF háromszög E pontra illeszkedő belső szögfelezőjén, azt kell megállapítanunk, hogy a (megfelelő nagyságú tömegekkel rendelkező) nulldimenziós DEF háromszög tömegközéppontja a háromszög belső szögfelezőinek közös pontja kell legyen. Geometriából ismerjük, hogy ilyen pont csak egy van, és az a DEF háromszögbe írható kör középpontja.
Az egydimenziós háromszög súlypontja tehát nem a geometriában értelmezett súlypont, vagyis nem a háromszög súlyvonalainak metszéspontja, hanem a háromszög oldalfelező pontjai által meghatározott háromszögbe írható kör középpontja.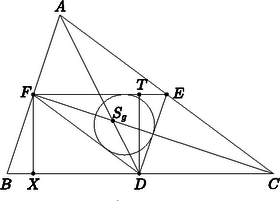
 
 

2. ábra
 

A geometriából azt is ismerjük, hogy a háromszög súlypontja a három oldal közül a leghosszabb oldalhoz van a legközelebb. Belátható, hogy az egydimenziós háromszög súlypontja is a leghosszabb oldalhoz van a legközelebb. A továbbiakban kimutatjuk, hogy az egydimenziós háromszög súlypontja közelebb van a leghosszabb oldalhoz (ha van a háromszögnek leghosszabb oldala), mint a háromszög súlyvonalainak metszéspontja, vagyis a geometriailag értelmezett súlypont, és a két távolság csak a szabályos háromszögben egyezik meg.
Tekintsük a 2. ábrát, amelyen az ABC háromszög két súlyvonalát (AD, illetve CF) és a geometriában értelmezett Sg súlypontját, valamint az oldalfelező pontjai által meghatározott DEF háromszögének a leghosszabb oldalhoz tartozó DT=FX magasságát is ábrázoltuk. Mint azt a matematikából ismerjük, a DEF háromszög beírható körének sugara r=t/s, ahol t a háromszög területe, azaz
t=a2⋅DT2=a⋅DT4
amelyben DT az EF=a2 hosszúságú, leghosszabb oldalhoz tartozó magasság, s pedig a DEF háromszög félkerülete:
s=a2+b2+c22=a+b+c4.

Láttuk, hogy az eredeti egydimenziós ABC háromszög tömegközéppontja a háromszög leghosszabb BC oldalától DT-r távolságban van. Súlyvonalainak metszéspontja ugyanezen oldaltól 23⋅XF=23⋅DT távolságra van, mert a súlyvonalak harmadolják egymást. Azt állítjuk tehát, hogy DT-r≤23⋅DT. Ennek igazolására írjuk be az egyenlőtlenség bal oldalába az előzőekben már felírt
r=ts=a⋅DTa+b+c
kifejezést. Egyszerűsítve DT-vel, amely nem lehet nulla, egyenlőtlenségünk a következő alakot ölti: 1-aa+b+c≤23. Minthogy a háromszög oldalai közül a a legnagyobb, az egyenlőtlenség bal oldalának értéke valóban legfeljebb 2/3. Egyenlőség akkor áll fenn, ha a=b=c, vagyis ha a háromszög szabályos. Ezzel igazoltuk állításunkat.
Hasonló módon igazolható, hogy az egydimenziós háromszög tömegközéppontja a legrövidebb c oldaltól messzebb van, mint a geometriai súlypont és ugyanezen oldal távolsága. A középső hosszúságú b oldaltól az egydimenziós háromszög súlypontja lehet közelebb is és lehet távolabb is, mint a geometriai súlypont, sőt, a két távolság éppen egybe is eshet, ha fennáll a b=(a+b)/2 összefüggés. Ez az eset fordult elő az idézett OKTV. I. fordulójában, a II. kategória 4. feladatánál, amely így szólt:
 
Az a, b, c oldalhosszúságú derékszögű háromszög oldalai azonos anyagú vékony rudakból állnak, amelyek mereven kapcsolódnak egymáshoz. A b oldalával vízszintes felületre illeszkedő függőleges síkú háromszög labilis egyensúlyi helyzetéből eldől.
a) Mekkora sebességgel éri el a B csúcs a vízszintes felületet, ha a dőlés közben a háromszög nem csúszik meg. (A b oldal súrlódásmentes csuklóval van rögzítve.)
b) Hol és mekkora sebességgel érkezne a B csúcs a vízszintes felülethez, ha a b oldal szabadon csúszhatna, és minden súrlódás elhanyagolható lenne? (a=30cm, c=50cm.)
 
A megoldás során több versenyző a háromszög súlypontját automatikusan, minden kisérő megjegyzés nélkül (a cikkben leírtak szerint elvileg hibásan!) ott vette fel, ahol a geometriailag értelmezett súlypont van, vagyis a súlyvonalak metszéspontjában. Ez a pont a b=40cm-es oldaltól 10 cm távolságra van. A háromszög fizikai értelemben vett igazi súlypontja nem esik egybe a súlyvonalak metszéspontjával, de az is éppen 10 cm távolságra van a b oldaltól, így ez az elvi hiba a további számítások eredményét nem rontotta el. A véletlen egybeesés azért fordult elő, mert a megadott adatokkal b éppen a másik két oldal számtani közepével egyezett meg. Ha a háromszög a leghosszabb, c=50cm-es oldalával illeszkedett volna a síkra, akkor a kétféle súlypont összekeverése numerikusan is észrevehető hibát okozott volna (a helyes 7 cm helyett 8 cm-rel számoltak volna).
Érdekes feladat lehet a különböző ,,dimenziójú'' háromszögek mintájára a négy tömegpontból álló nulldimenziós, rudakból összerakott egydimenziós, vékony lemezekből készített kétdimenziós és végül a tömör, háromdimenziós tetraéder súlypontjának megkeresése; ennek a problémának a tanulmányozását azonban az Olvasóra hagyjuk.