|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A lapunkban megjelenő feladatok mintamegoldásainak írása közben sokszor jelent problémát annak eldöntése, hogy egy állítás közismert-e, s ezért nem kell bizonyítani, vagy pedig nem az, és ezért a bizonyítását is le kell írni. Különösen így volt ez a B. 3478. feladatnál, amit nagyon sokféleképpen lehetett megoldani.
E cikknek az a célja, hogy a háromszögekkel kapcsolatos néhány állítás egyszerű bizonyításait összegyűjtse. A háromszögekkel kapcsolatban rengeteg tétel van, mi csak azokkal foglalkozunk, amelyek kapcsolódnak a háromszöghöz tartozó körökhöz. Ezeknek is csak egy részét ismertetjük, egyáltalán nem foglalkozunk pl. a Feuerbach körrel. Az érdeklődő olvasó további szép tételeket találhat az irodalomjegyzékben szereplő könyvekben.
A háromszögben a három oldal, csúcs, szög stb. szerepe szimmetrikus. Ezért állításainkban és bizonyításainkban a rövidség kedvéért sokszor csak szerepel. Ezeket persze úgy kell érteni, hogy a háromszög tetszőleges oldalára, csúcsára, szögére igaz a megfelelő állítás.
Legyenek a háromszög csúcsai , , , oldalai , , , szögei , , , a szokásos jelölésekkel a háromszög területét jelölje , kerületét , a beírható kör sugara legyen , a hozzáírt körök sugarai , , , a háromszög köré írható kör sugara , végül ezen körök középpontjai legyenek rendre , , , és (1. ábra).
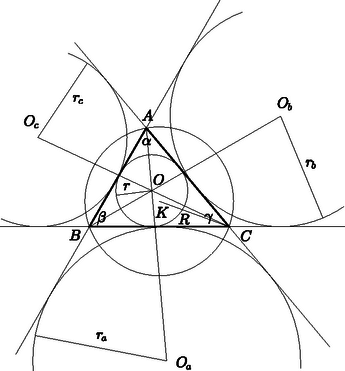 1. ábra
Első állításunkat általánosított szinusztételnek is szokás nevezni.
1. állítás. .
Bizonyítás. Messe a háromszög köré írható körének átmérője a kört másodszor az pontban. Ekkor . Ha , akkor , az állítás nyilvánvaló (2/1. ábra). Ha nem derékszög, akkor (2/2. ábra), vagy (2/3. ábra), de felhasználva a összefüggést, valamint azt, hogy a háromszög -nél lévő szöge Thalész tétele miatt derékszög, mindig teljesül, hogy . | |
Ha a T=b⋅c⋅sinα2 területképletben az oldalakat kifejezzük az 1. állításból adódó 2Rsinβ-val, illetve 2Rsinγ-val, akkor a következőt kapjuk:
3. állítás. T=2R2sinαsinβsinγ.
Tudjuk, hogy O a háromszög három belső szögfelezőjének, Oa, Ob és Oc pedig két-két külső- és egy-egy belső szögfelezőjének a metszéspontja. Mivel a háromszög bármely csúcsához tartozó külső és belső szögfelező merőleges egymásra, ezért igaz a következő:
4. állítás. Az OaObOc háromszög magasságpontja O, magasságvonalai pedig megegyeznek az ABC háromszög belső szögfelezőivel.
Ebből következik, hogy az OBOaC négyszög húrnégyszög, mert B-nél és C-nél lévő szögei egyaránt derékszögek. A négyszöget az OOa átló két közös átfogójú derékszögű háromszögre bontja, ezért a négyszög köré írható kör középpontja az OOa szakasz felezőpontja. A négyszög köré írt kört megrajzolva (3. ábra) látszik, hogy OCB∢=OOaB∢ és OBC∢=OOaC∢, mert az egy íven nyugvó kerületi szögek egyenlőek. Vagyis BOaC∢=OOaB∢+OOaC∢=γ2+β2. Ezzel bebizonyítottuk a következőt:
5. állítás. Az OaObOc háromszög szögei rendre: β+γ2, γ+α2 és α+β2.
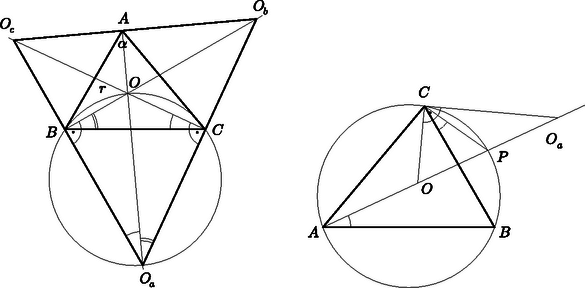 3. ábra 4. ábra
Következő állításunk az eddigieknél kevésbé ismert (bár megtalálható a Geometriai feladatok gyűjteménye I. kötetében).
6. állítás. A háromszög köré írható kör felezi a beírható kör középpontját a hozzáírható körök középpontjaival összekötő szakaszokat.
Bizonyítás. Messe a köré írható kör az OOa szakaszt P-ben (4. ábra). (Mivel COaB∢=β+γ2<180∘-α=180∘-CAB∢, ezért Oa a köré írható körön kívül helyezkedik el, vagyis P mindig létrejön.) Ekkor PCB∢=PAB∢, mert mindkettő a PB ívhez tartozó kerületi szög. Ezért PCO∢=PCB∢+BCO∢=α2+γ2. Az OCOa háromszögben C-nél derékszög van, az Oa-nál lévő szögről már láttuk, hogy β2, ezért az O-nál lévő szög 90∘-β2=α2+γ2. Vagyis POC∢=PCO∢, tehát a POC háromszög egyenlő szárú, PO=PC. Ugyanígy láthatjuk be, hogy PO=PB. Ez azt jelenti, hogy az OBC háromszög köré írható kör középpontja P. Ez a kör azonban megegyezik az OBOaC húrnégyszög köré írható körrel, hiszen mindkét sokszögnek csúcsa O, B és C. Azt viszont a 4. állítás után beláttuk, hogy az OBOaC köré írható kör középpontja az OOa szakasz felezőpontja. Tehát P felezi OOa-t. |
7. állítás. A hozzáírt körök középpontjai által meghatározott háromszög köré írható körének sugara 2R.
Bizonyítás. Ha az O pontból kétszeresére nagyítjuk a köré írható kört, akkor a keletkezett 2R sugarú kör az 5. állítás miatt átmegy az Oa, Ob és Oc pontok mindegyikén (5. ábra). |
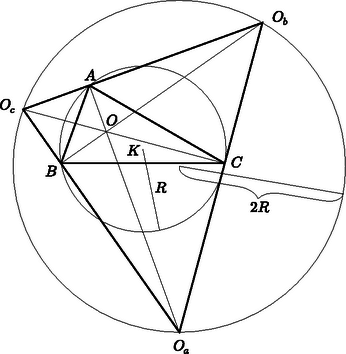 5. ábra
(A 6. és 7. állításokat a fentieknél egyszerűbben beláthatja az, aki ismeri a Feuerbach-kör tulajdonságait ‐ lásd pl. [2], 69‐70. oldal ‐, a 3. állításból ugyanis következik, hogy az OaObOc háromszög Feuerbach-köre megegyezik az ABC háromszög körülírt körével. Ebből pedig nemcsak 6. és 7. következik, hanem az is, hogy a körülírt kör felezi a hozzáírt körök középpontjai által meghatározott szakaszokat.)
A továbbiakban a beírt és a hozzáírt körök sugarait fejezzük ki az oldalakkal és a területtel. Ehhez először meghatározzuk ezen körök és az oldalegyenesek érintési pontjainak a háromszög csúcsaitól való távolságát. Jelöljük az érintési pontokat a 6. ábrán látható módon D, E, F, G, H, I-vel. Mivel egy külső pontból egy körhöz húzott két érintőszakasz hossza egyenlő, ezért AH=AI, BG=BI és CH=CG, továbbá a 6. ábra jelöléseinek megfelelően AE=AF=x, BD=BF=y és CD=CE=z.
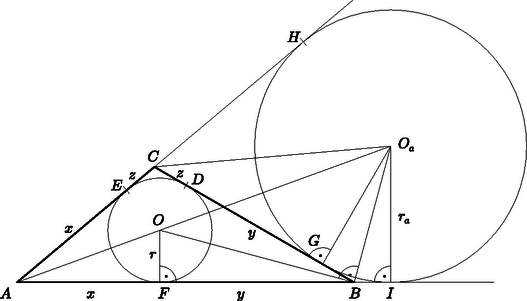 6. ábra
Az x+y=c, y+z=a és z+x=b összefüggésekből következik, hogy 2x+2y+2z=a+b+c=2s, azaz x+y+z=s, és így A hozzáírt körhöz húzott érintőszakaszokra pedig | 2AH=AH+AI=(AC+CG)+(AB+BG)=AC+AB+BC=2s, |
tehát | AH=AI=s,BG=BI=s-c,CH=CG=s-b. | (2) |
8. állítás. T=r⋅s=ra(s-a)=rb(s-b)=rc(s-c).
Bizonyítás. Az ABC háromszög területe megegyezik az OAB, OBC és OCA háromszögek területének összegével. E három háromszög O-hoz tartozó magasságai r hosszúak, így területeik rendre c⋅r2, a⋅r2 és b⋅r2. Ezeket összeadva kapjuk, hogy T=r⋅s.
A hozzáírt kör esetén azt kell felhasználnunk, hogy az ABC háromszög területe megegyezik az OaAB és OaCA háromszögek területei összegének és az OaBC háromszög területének különbségével, azaz | T=c⋅ra2+b⋅ra2-a⋅ra2=ra(s-a). |
9. állítás. A beírt kör sugarának reciproka megegyezik a hozzáírt körök sugarának reciprokösszegével.
Bizonyítás. A 8. állítás szerint | 1ra+1rb+1rc=s-aT+s-bT+s-cT=3s-(a+b+c)T=sT=1r. |
10. állítás (Héron képlete). T=s(s-a)(s-b)(s-c).
Bizonyítás. A 6. ábrán látható OBF és BOaI háromszögek hasonlóak, mert F-nél illetve I-nél derékszögük van, a külső és a belső szögfelezők merőlegessége miatt pedig OBF∢ és BOaI∢ merőleges szárú hegyesszögek. Ezért a két háromszög megfelelő oldalainak aránya megegyezik: Ezt (1), (2) és a 8. állítás felhasználásával átalakítva: | rs-b=s-cra,azaz(s-b)(s-c)=r⋅ra=Ts⋅Ts-a, |
amiből T2=s(s-a)(s-b)(s-c) adódik. |
11. állítás. 4R=ra+rb+rc-r.
Bizonyítás. A 2. és a 8. állítás alapján elegendő azt megmutatnunk, hogy |
abcT=Ts-a+Ts-b+Ts-c-Ts. |
 PDF | MathML
PDF | MathML 


