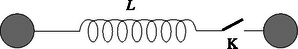|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az I. kategória (szakközépiskolások) feladatai 1. feladat. Egyenletesen növekvő gyorsulással mozgó test gyorsulása -kor , t1=1s-kor a1=3m/s2. A sebessége t0=0-kor v0=1m/s.
a) Mekkora lesz a sebessége t2=10s-kor?
b) Határozzuk meg a mozgás v-t függvényét, majd vázoljuk fel egy v-t koordináta-rendszerben!
c) Becsüljük meg, hogy mekkora utat fut be a test a 0<t<10 s-os intervallum első és az utolsó másodpercében!
Megoldás. A gyorsulás‐idő diagram az 1. ábrán látható. A test gyorsulása t2=10s-kor a2=12m/s2. A sebességváltozást a grafikon alatti (trapéz alakú) terület nagysága adja meg: Δv=70m/s, és mivel a testnek kezdősebessége is volt, a t2 idő alatt elért sebessége: 71m/s.
b) A fentihez hasonló számítás elvégezve (de t2 helyére egy általános t időt írva) megkapjuk a mozgás v-t függvényét. Ez (az SI rendszerben számolt mértékegységek elhagyásával) Ez a függvény egy transzformált normál-parabola (2. ábra).
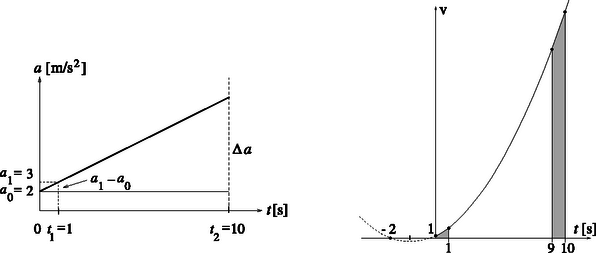 1. ábra 2. ábra 1. ábra 2. ábra
c) A 0<t<1 s és a 9s<t<10s időközökben megtett utak a fenti v-t grafikon megfelelő területeinek meghatározásával számíthatók. Mivel ilyen rövid időközökhöz tartozó értékek igen jó közelíthetők egyenes szakaszokkal, lényegében egy-egy trapéz területének meghatározására egyszerűsödik a feladat. Eszerint az első másodpercben közelítőleg 2,25m, a tizedikben pedig kb. 65,25m utat tesz meg a test.
Megjegyzés: A közelítés jogossága ellenőrizhető az integrálással kapott pontos értékkel való összehasonlítás útján. Ezzel a két útszakasz hossza: s1=2,17m, illetve s2=65,17m. A relatív hiba az első esetben kb. 4%, a másodiknál pedig 0,1%.
2. feladat. Vízszintes tengelyű, M tömegű, R sugarú henger súrlódásmentesen foroghat. A hengerpalástra tekert fonál másik végéhez egy m tömegű nehezéket erősítettünk. Kezdetben a fonál függőleges egyenest alkot, feszítetlen állapotban. A nehezéket erről a szintről h-val magasabbra emeljük, majd kezdősebesség nélkül elengedjük. Az elengedéstől szá- mítva mennyi idő múlva tesz meg a nehezék 2h utat? (A fonál nyújthatatlan, a kölcsönhatás pillanatszerű és abszolút rugalmatlan. Adatok: M=2kg, R=0,2 m, m=3 kg, h=1,2m.)
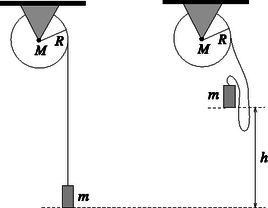 3. ábra 3. ábra
Megoldás. A nehezék sebessége ,,ütközéskor'' v=2gh. A fonál pillanatszerű erőlökése alatt a nehézségi erő elhanyagolható, vagyis a rendszernek a forgástengelyre vonatkoztatott perdülete megmarad: A fonál nyújthatatlansága (kényszerfeltétel) miatt u=Rω. Ezekből az egyenletekből
Innen kezdve a nehezék u kezdősebességgel, egyenletesen gyorsulva folytatja útját. A nehezék mozgásegyenlete: a henger forgásának egyenlete: ahol β=a/R. Ezekből a nehezék gyorsulása:
A mozgás első szakaszának megtételéhez szükséges idő: t1=2h/g=0,495s. A mozgás második szakaszának idejét az úttörvényből kapjuk: h=ut+12at2, ahonnan A 2h út megtételéhez szükséges idő t=t1+t2=0,76s.
3. feladat. Két, igen nagy távolságban elhelyezett R sugarú fémgömböt egy L induktivitású tekerccsel kötünk össze a 4. ábra szerint. Az egyik gömbnek töltést adunk. A kapcsoló zárása után mennyi idő múlva csökken a töltés ezen a gömbön a felére? Mennyi idő múlva lesz újra annyi, mint kezdetben?
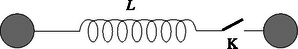 4. ábra 4. ábra
Megoldás. Ha az első gömb töltése kezdetben Q, akkor a potenciálja A másik gömb potenciálja kezdetben 0. Mivel a tekercs két vége között ily módon potenciálkülönbség van, a tekercsen áram kezd folyni, azaz a töltés átáramlik az egyik gömbről a másikra. Világos ebből, hogy a rendszer egy rezgőkör, amelyben a kondenzátort a fémgömbök képezik.
Megjegyzés. Egy ideális rezgőkörben csillapítatlan harmonikus rezgések jönnek létre, vagyis a töltés az egyik fegyverzetről teljes egészében átáramlik a másikra, majd maradéktalanul visszaáramlik az elsőre. A továbbiakban a rendszert ideális rezgőkörrel közelítjük, vagyis elhanyagoljuk az egy periódus alatti energiaveszteséget, noha részben a Joule-hő, részben a dipólantenna-sugárzás ténylegesen csökkenti a rendszer energiáját.
Mekkora lesz a ,,helyettesítő kondenzátor'' kapacitása? (Figyelembe kell venni, hogy most az eredő töltés nem nulla.) A következő gondolatmenettel juthatunk célhoz: mondjuk azt, hogy a Q töltés az első gömbön Q/2 és Q/2 töltések, a második gömbön a 0 töltés Q/2 és -Q/2 töltések alakjában van jelen. A két gömb Q/2 töltéseitől származó potenciálok különbsége 0, míg a Q/2 és -Q/2 (egyik és másik gömb) töltésektől származó potenciálok különbsége Umax=U0. Eszerint a helyettesítő kondenzátor töltése Q/2, feszültsége pedig U0, tehát a kapacitása: Rezgőkörünk periódusideje eszerint: Ennyi idő múlva lesz az első gömbön ismét a kezdeti töltés.
Amikor az első gömb töltése Q/2, akkor a másodiké is annyi, tehát a potenciálkülönbség a tekercsen 0, az eltelt idő eszerint a negyed periódus:
A II. kategória feladatai
1. feladat. Egy ℓ hosszúságú, homogén anyageloszlású kötél vége R sugarú henger tetejére van kikötve. A kötelet hirtelen elengedjük. Mekkora gyorsulással indul meg a kötél? Súrlódás nincs, a henger rögzítve van. Adjuk meg a kezdeti gyorsulás nagyságát, ha a kötél hossza Rπ/4, Rπ/2, 2R.
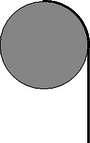 5. ábra 5. ábra
Megoldás. A kötelet a nehézségi erő és a súrlódásmentes felület által kifejtett kényszererő gyorsítja. A nyújthatatlan kötél minden darabkájának a kötél ottani érintője irányába mutató és azonos nagyságú tangenciális gyorsulása van. A kezdeti pillanatban ugyanis a sebesség még nulla, így centripetális gyorsulással nem kell számolnunk.
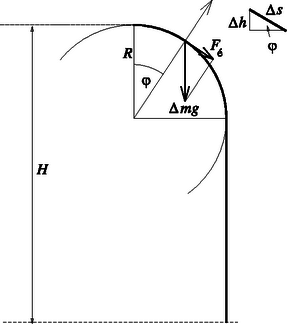 6. ábra 6. ábra
Osszuk fel a kötelet kicsiny Δs hosszú darabokra, és a függőleges irány és a kötéldarabkához húzott sugár közti szög legyen φ (6. ábra)! Mivel a kényszererő merőleges a kényszerfelületre, a kötéldarabkára ható eredő külső erő ‐ érintő irányú lévén ‐ a nehézségi erő érintőirányú vetületével azonos. (A kötéldarabkákra a szomszédok által kifejtett erő is hat, a belső erők azonban az összegezés során kiesnek.) A Δs hosszúságú kötéldarabkára ható nehézségi erő érintőirányú komponensének nagysága: ahol M a kötél tömege. A 6. ábráról leolvasható, hogy tehát Az egész kötélre ható külső erő érintőirányú komponenseinek összege: ahol H a kötél függőleges vetületének hossza.
A kötél kezdőpillanatbeli gyorsulása tehát: a=F/M=Hg/ℓ.
Ha ℓ=Rπ/4, akkor H=R(1-2/2) és
Ha ℓ=Rπ/2, akkor H=R és
Ha ℓ=2R, akkor H=R(3-π/2) és
2. feladat. Könnyen mozgó dugattyúval elzárt hengerben m=180 g tömegű, héliumból és hidrogénből álló gázkeverékkel állandó nyomáson Q=156kJ hőt közlünk. Ennek hatására a gázkeverék 56kJ munkát végzett. Hány g hidrogén volt a hengerben? Mekkora a gázkeverék hőmérsékletváltozása?
Megoldás. Jelöljük a hidrogéngáz tömegét m1-gyel, a héliumgáz tömegét pedig m2-vel (m1+m2=180 g). Az I. főtételből a belső energia megváltozása: | ΔE=Q+W=Q-Wgáz=156kJ-56kJ=100kJ. |
A gáz állandó (külső) nyomáson tágul, a folyamat tehát izobár, így továbbá ahol f1,2 és N1,2 a szabadsági fokok számát, illetve a molekulák számát jelöli. A fenti két egyenletből | ΔE=(f12N1+f22N2)pΔVN1+N2=(f12N1+f22N2)WgázN1+N2, |
majd ebből | 2ΔEWgáz=f1N1+f2N2N1+N2,azaz20056=5N1+3N2N1+N2 |
következik. Innen a molekulák számának arányára N1/N2=0,4, a tömegarányra pedig (a móltömegek figyelembe vételével) adódik. Mivel m=m1+m2=180 g, a hidrogéngáz tömege m1=m/6=30 g.
A hőmérsékletváltozás az állapotegyenletből számítható: | pΔV=Wgáz=(N1+N2)RΔT=(m1M1+m2M2)RΔT, |
ahonnan | ΔT=Wgáz⋅M1M2R(m1M2+m2M1)=128K. |
3. feladat. Tömegspektrográf A1 résén különböző sebességgel kirepülő Cl- ionok először egymásra merőleges elektromos és mágneses mezőn, majd az A2 rés után csak mágneses mezőn haladnak át. A 35Cl és 37Cl izotópok egymástól Δx=4cm távolságban csapódnak a fotólemezbe. A mágneses mező indukciója B=0,02T.
a) Mekkora sebességgel haladnak át a Cl izotópok az A2 résen?
b) Milyen nagyságú és irányú elektromos térerősség van az A1 és A2 rés között?
Megoldás. a) A 7. ábrán látható, hogy a klorid-ionok egyenes pályán haladnak az ionforrástól az A1 és az A2 réseken keresztül. Ez (az ionforrásból általában különböző sebességgel induló) ionok közül csak azok számára lehetséges, amelyek jól meghatározott sebességgel rendelkeznek. A többi ion a mágneses térbe jutva eltérül az egyenes iránytól. A keresztezett elektrosztatikai és mágneses tér ezek szerint ,,sebességszűrőként'' szerepel, az A2 rés után tehát már csak egyetlen sebességgel kell számolnunk.
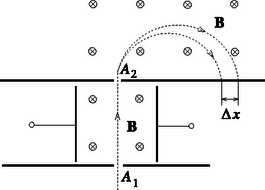 7. ábra 7. ábra
Az A2 rés után már tisztán mágneses mező van, amelynek indukciójára merőlegesen lépnek be az ionok. Itt egyenletes körmozgással haladnak a becsapódásig. A mágneses Lorentz-erő adja a centripetális eredő erőt. A mozgásegyenlet: amelyből a két izotóp pályasugara: | r1=m1vBe,illetver2=m2vBe. |
Felhasználva, hogy | Δx=2(r2-r1)=2vBe(m2-m1)=2vBeΔm, |
a kérdéses sebesség:
b) A sebességszűrő csak azokat a részecskéket nem téríti el, amelyekre az elektromos és a mágneses erők ellentétes irányúak és egyenlő abszolút értékűek: eE=Bev, ebből az elektromos érerősség nagysága: Az elektromos mező homogén, és a térerősség-vektora balról jobbra mutat.
A III. kategória feladatai 1. feladat. Az L hosszúságú vékony pálca az asztal lapja felett H magasságból vízszintes helyzetben szabadon esik, és az egyik vége éppen az asztal sarkával ütközik. Az ütközés abszolút rugalmas és pillanatszerű. Az ütközéstől számítva mennyi idő alatt tesz meg a pálca egy teljes fordulatot? Hol lesz ekkor a pálca középpontja? (H=80cm, L=40cm, és számoljunk g=10m/s-mal!)
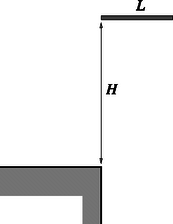 8. ábra 8. ábra 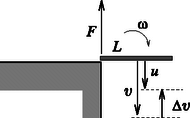 9. ábra 9. ábra
Megoldás. Az asztallal való ,,pillanatszerű'' (valójában ,,nagyon rövid'' Δt ideig tartó) kölcsönhatás során csak függőleges erők hatnak (9. ábra). Az impulzustétel: Itt F az asztal által függőlegesen felfele kifejtett (Δt kicsinysége miatt igen nagy) erőt jelöli, amely mellett a pálcára ható nehézségi erő elhanyagolható; v=2gH≈4m/s a pálca tömegközéppontjának ütközés előtti, u pedig az ütközés utáni sebessége.
A perdülettétel a pálca tömegközéppontjára felírva: (ω a pálca szögsebessége az ütközés után, Θ=112mL2.)
Az ütközés tökéletesen rugalmas, így alkalmazható a mechanikai energia megmaradásának tétele is:
Az (1)‐(3) egyenletrendszer megoldása illetve Egy teljes fordulat ideje (5) szerint ennyi idő alatt a tömegközéppont | Δy=uT+12gT2=π3⋅L(1+π3⋅LH)=0,63m |
utat tesz meg. (Érdekes, hogy Δy nem függ g számszerű értékétől.) 2. feladat. Azonos a II. kategória 2. feladatával.
3. feladat. Egy katódsugárcsőben a katódból elhanyagolható kezdősebességgel kilépő elektronok U0=182V feszültségen gyorsulnak, majd egy keskeny, lyukas kondenzátoron haladnak keresztül, amelyre a 10. ábrán látható nagyfrekvenciás négyszögrezgés alakú feszültség van kapcsolva, amelynek csúcsfeszültsége UM=102,4V, és periódusideje T=5⋅10-9s.
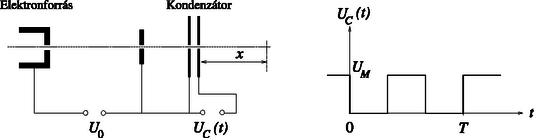 10. ábra 10. ábra
Ha a négyszögrezgés nincs bekapcsolva, akkor a kondenzátoron áthaladó elektronnyaláb állandó áramerőssége I=1μA. Ábrázoljuk áramerősség ‐ idő grafikonon az áramerősség időbeli változását a cső azon helyein, amelyek a kondenzátortól x1=10cm, x2=20cm, x3=15cm távolságra vannak, ha a négyszögrezgés be van kapcsolva! (A négyszögrezgés polaritása olyan, hogy UC(t)>0 esetén a kondenzátoron áthaladó elektronok sebessége növekszik. A kondenzátor olyan keskeny, hogy az elektronok elhanyagolható idő alatt áthaladnak rajta.)
Megoldás. A négyszögrezgés periódusideje T=5ns. A négyszögrezgés első félperiódusában az elektronok sebességgel indulnak a kondenzátortól, míg a második félperiódusban az elektronok sebessége.
A kondenzátor utáni térrészben ,,lassú'' és ,,gyors'' töltéscsomagok haladnak. A lassúak hosszúságúak, a gyorsak hosszúságúak. (Mindkét típusú töltéscsomag mozgása egyenletesnek tekinthető, hiszen az elektronok közötti kölcsönhatás a megadott kicsiny áramerősség mellett jó közelítéssel elhanyagolható.)
A gyors töltéscsomagok utolérhetik a lassúakat, ezért egy adott pillanatban egy adott helyen lehetséges, hogy a kétféle töltéscsomag egyszerre van jelen, előfordulhat, hogy csak az egyik van ott, és az is lehetséges, hogy éppen egyik féle sincs jelen!
A kétféle töltéscsomagban azonos számú elektron halad. A kondenzátor bal oldali lemezéhez egyenlő (T/2) idők alatt egyenlő számú elektron érkezik, ezek vagy felgyorsulnak (ekkor a csomag térbeli kiterjedése megnyúlik), vagy változatlan sebességgel és hosszban haladnak tovább. A kétféle töltéscsomagban haladó elektronok száma:
A tér egy adott pontján mindkét sebességű töltéscsomag azonos idő alatt halad keresztül. Ha a tér valamely pontjában csak az egyikféle töltéscsomag van jelen, akkor ott I1=1μA az áramerősség. Ha mindkétféle töltéscsomag jelen van, akkor az áramerősség I2=2μA. Az utolérések jól áttekinthetők az elemi számításokkal is felrajzolható x-t grafikonon (11. ábra).
Az út‐idő grafikon alapján a kérdezett helyek áramerősség - idő grafikonjai is megkaphatók (12. ábra). Látható, hogy x1=10cm-nél éppen ,,egymásracsúszott'' a két töltéscsomag, x2=20cm-nél a csomagok időbeli eltolódása T, tehát az áramerősség ugyanolyan, mint közvetlenül a kondenzátor után, végül x3=15cm-nél a csomagok időbeli eltolódása T/4.
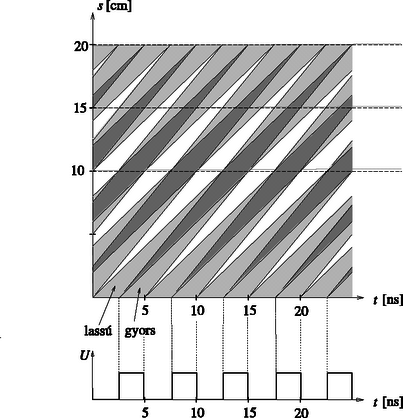 11. ábra 11. ábra  12. ábra 12. ábra
A fizika I. kategória végeredménye
| 1. | Fábián Viktor (Budapest, Trefort Á. Kéttannyelvű Műszaki Szki., 11. évf.),
tanára: Fülöp László; |
| 2. | Hoffer János Pál (Kecskemét, Kandó K. Szki., 12. évf.),
tanára: Jusztin Zsuzsanna; |
| 3. | Ács Donát (Budapest, Trefort Á. Kéttannyelvű Műszaki Szki., 11. évf.),
tanára: Fülöp László; |
4. Kiss Ferenc (Budapest, Puskás T. Távközlési Technikum, 11. évf.), tanára: Beregszászi Zoltán; 5. Sipos Barnabás (Budapest, Trefort Á. Kéttannyelvű Műszaki Szki., 11. évf.), tanára: Fülöp László; 6. Orosz Gyula (Budapest, Puskás T. Távközlési Technikum, 12. évf.), tanára: Alapiné Ecseri Éva; 7. Mendli Bálint (Budapest, Puskás T. Távközlési Technikum, 11. évf.), tanára: Beregszászi Zoltán; 8. Détári Gábor (Vác, Boronkay Gy. Műszaki Középisk. és Gimn., 12. évf.), tanára: Arany Tóth László; 9. Szökő Márton (Budapest, Trefort Á. Kéttannyelvű Műszaki Szki., 11. évf.), tanára: Fülöp László; 10. Juhász Gábor (Vác, Boronkay Gy. Műszaki Középisk. és Gimn., 11. évf.), tanára: Csomó József.
A fizika II. kategória végeredménye
| 1. | Pozsgay Balázs (Pécs, Magyar-német Nyelvű Iskolaközp. 11. évf.),
tanárai: Kotek László, Baumgärtner Annamária; |
| 2. | Siroki László (Debrecen, Fazekas M. Gimn., 11. évf.),
tanárai: Adorján László, Szegedi Ervin, Kopcsa József; |
| 3. | Béky Bence (Fazekas M. Főv. Gyak. Gimn., 11. évf.),
tanára: Horváth Gábor; |
4. Varjú Péter (Szeged, Radnóti M. Kís. Gimn., 12. évf.), tanára: Dudás Zoltánné; 5. Vizer Tibor (Kecskemét, Piarista Iskola, 12. évf.), tanárai: Szőke-Tóth Zsolt, Sebestyén László; 6. Nagy Márton (Budapest, Piarista Gimn., 11. évf.), tanárai: Urbán János, Futó Béla; 7. Hamar Gergő (Dombóvár, Illyés Gy. Gimn., 11. évf.), tanárai: Freller Miklós, Kotek László; 8. Gerencsér Balázs (Fazekas M. Főv. Gyak. Gimn., 11. évf.), tanára: Horváth Gábor; 9. Pápai Tivadar (Barcs, Dráva Völgye Középisk., 12. évf.), tanára: Horváth Ferenc; 10. Zalán Péter (Budapest, Fasori Evangélikus Gimn. 12. évf.), tanára: Mecseki Attila.
A fizika III. kategória végeredménye
| 1. | Horváth György (Fazekas M. Főv. Gyak. Gimn., 12. évf.),
tanárai: Takács Lajos, Horváth Gábor; |
| 2. | Nagy Ádám (Budapest, Szent István Gimn., 12. évf.),
tanára: Moór Ágnes; |
| 3. | Geresdi Attila (Pécs, Árpád Fejedelem Gimn., 11. évf.),
tanárai: Porkoláb Tamás, Györpál Elemérné; |
4. Schmidt András (Budapest, Szent István Gimn., 12. évf.), tanára: Moór Ágnes; 5. Horváth Ákos (Budapest, Berzsenyi D. Gimn., 12. évf.), tanára: Gyenes Gábor; 6. Ábel Dániel (Budapest, Németh László Gimn., 11. évf.), tanárai: Dégen Csaba, Zsigri Ferenc; 7. Dombai Péter (Szekszárd, Garay J. Gimn. 12. évf.), tanára: Jurisits József; 8. Ágas Attila (Keszthely, Vajda J. Gimn., 11. évf.), tanára: Farkas László; 9. Rénes Sándor (Szolnok, Verseghy F. Gimn., 12. évf.), tanára: Szécsiné Festő Hegedűs Margit; 10. Nagy Dávid (Kecskemét, Bányai Júlia Gimn., 12. évf.). |
 PDF | MathML
PDF | MathML