Kezdőlap


Cím:	Megoldásvázlatok, eredmények a 2002/1. sz. feladataihoz
Szerző(k):	Orosz Gyula
Füzet:	2002/február, 77 - 80. oldal	PDF \| MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Az $a$ , $b$ , $c$ , $x$ , $y$ , $z$ valós számokra $\frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0$ és $\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$ . Mennyi $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} + \frac{z^{2}}{c^{2}}$ értéke?

Megoldás.

a, b, c, x, y, z \neq 0

. Alkalmazzuk pl. az

u = \frac{x}{a}

v = \frac{y}{b}

w = \frac{z}{c}

helyettesítést; ekkor a két egyenlet

u + v + w = 1

és

\frac{1}{u} + \frac{1}{v} + \frac{1}{w} = 0

alakba írható, s

u^{2} + v^{2} + w^{2}

értéke a kérdés.

\frac{1}{u} + \frac{1}{v} + \frac{1}{w} = \frac{u v + v w + u w}{u v w} = 0

miatt

u v + v w + u w = 0

; az

{(u + v + w)}^{2} = u^{2} + v^{2} + w^{2} + 2 (u v + v w + u w)

átalakításból kapjuk, hogy

u^{2} + v^{2} + w^{2} = 1

Megjegyzés. Érdemes megvizsgálni, léteznek-e egyáltalán a feladat feltételeinek megfelelő

u

v

w

számok.
Mivel

u + v = 1 - w

és

u v = - w (u + v) = - w (1 - w) = w^{2} - w

, így a

t^{2} + (w - 1) t + w^{2} - w = 0

egyenlet két gyöke

t_{1} = u

és

t_{2} = v

. (A gyökök és együtthatók közötti összefüggések alapján.) Az egyenlet diszkriminánsa

\begin{matrix} D = {(w - 1)}^{2} - 4 (w^{2} - w) = (w - 1) (- 3 w - 1) = - 3 (w - 1) (w + \frac{1}{3}); - \frac{1}{3} \leq w \leq 1 \end{matrix}

esetén

D \geq 0

, tehát találhatók megfelelő

u

v

számok. Például

w = - \frac{1}{3}

u = v = \frac{2}{3}

megfelelő.

2. Oldjuk meg a

4 \cdot log_{x} 2 = 7 + 2 \cdot log_{2} x

egyenletet a valós számok halmazán!

Megoldás. Az egyenlet alaphalmaza

x > 0

x \neq 1

. Áttérve azonos alapú logaritmusokra:

4 \cdot \frac{log_{2} 2}{log_{2} x} = 7 + 2 \cdot log_{2} x

. Az

a = log_{2} x

helyettesítéssel egyenletünk

\frac{4}{a} = 7 + 2 a

alakú lesz, melyet átalakítva a

2 a^{2} + 7 a - 4 = 0

másodfokú egyenletet kapjuk.

a_{1} = \frac{1}{2}

a_{2} = - 4

; visszahelyettesítve

x

-re

x_{1} = \sqrt[]{2}

x_{2} = 2^{- 4} = \frac{1}{16}

. Mindkét gyök kielégíti az eredeti egyenletet.

3. Az

x^{3} + x^{2} - 14 x + m = 0

egyenlet egyik gyöke

3

. Határozzuk meg az

m

valós paraméter és a másik két gyök értékét!

Megoldás. Az

x_{1} = 3

helyettesítés után

3^{3} + 3^{2} - 14 \cdot 3 + m = 0

, innen

m = 6

. Az

x - 3

gyöktényezőt kiemelve

x^{3} + x^{2} - 14 x + 6 = (x - 3) (x^{2} + 4 x - 2) = 0

. A második tényező zérushelyei

x_{2} = - 2 + \sqrt[]{6}

, ill.

x_{3} = - 2 - \sqrt[]{6}

4. Az

A B C

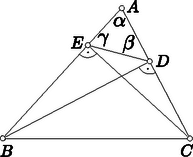
háromszögben a

B

csúcsból húzott magasságvonal az

A C

egyenest a

D

pontban, a

C

-ből húzott magasságvonal az

A B

egyenest az

E

pontban metszi. Mekkora a

D E

szakasz hossza, ha

C A B ∢ = 70^{\circ}

A B = 12 cm

A C = 10 cm

Megoldás. Jelöljük az adott háromszög

A

B

C

csúcsnál lévő szögeit hagyományosan

α

β

γ

-val, az

A B

B C

A C

oldalak hosszát

c

a

b

-vel; így

α = 70^{\circ}

c = 12 cm

b = 10 cm

.
Készítsünk ábrát!

Észrevehetjük, hogy

B C D E

húrnégyszög, hiszen a

B C

oldal

E

-ből és

D

-ből is

90^{\circ}

alatt látszik. (A négyszög köré írt kör középpontja a

B C

oldal felezőpontja.) A húrnégyszögek szemközti szögeinek összege

180^{\circ}

, ezért

B E D ∢ = 180^{\circ} - γ

, s így

D E A ∢ = γ

(ábra). Hasonlóan kapjuk, hogy

E D A ∢ = β

. Az

A B C

és

A D E

háromszögek tehát hasonlók, mert szögeik megegyeznek. A megfelelő oldalak arányát felírva

\frac{D E}{B C} = \frac{A E}{A C}

, s mivel az

A E C

derékszögű háromszögből

\frac{A E}{A C} = cos α

D E = B C \cdot cos α = a \cdot cos α

.
A háromszög

B C = a

oldalát a koszinusz-tétel felhasználásával számíthatjuk ki:

\begin{matrix} a^{2} = b^{2} + c^{2} - 2 \cdot b \cdot c \cdot cos α = 100 + 144 - 2 \cdot 10 \cdot 12 \cdot cos 70^{\circ}, \end{matrix}

a \approx 12, 72 cm

, s innen

D E = a \cdot cos α \approx 4, 35 cm

Megjegyzés. A három magasságvonal talppontja (ábránkon kettőt jelöltünk:

D

és

E

) meghatározza az ún. talpponti háromszöget. Meggondolásainkból következik, hogy hegyesszögű háromszögben a talpponti háromszög kerülete

a \cdot cos α + b \cdot cos β + c \cdot cos γ

5. Oldjuk meg a

cos (2 x) - 3 cos x + 2 \leq 0

egyenlőtlenséget a valós számok halmazán!

Megoldás. Felhasználva a

cos 2 x

-re vonatkozó addíciós tételt és a trigonometria alapegyenletét:

cos 2 x = cos^{2} x - sin^{2} x = cos^{2} x - (1 - cos^{2} x) = 2 cos^{2} x - 1

. Visszahelyettesítés után az eredeti egyenlőtlenség

2 cos^{2} x - 3 cos x + 1 \leq 0

alakú lesz, s ez a

cos x

változóban másodfokú. A két zérushely

{(cos x)}_{1} = 1

{(cos x)}_{2} = \frac{1}{2}

; a bal oldalt eszerint szorzattá alakítva kapjuk, hogy

2 (cos x - 1) (cos x - \frac{1}{2}) \leq 0

. Ennek megoldása

\frac{1}{2} \leq cos x \leq 1

. A

cos x \leq 1

egyenlőtlenség minden valós számra igaz,

\frac{1}{2} \leq cos x

pedig akkor teljesül, ha

- \frac{π}{3} + k \cdot 2 π \leq x \leq \frac{π}{3} + k \cdot 2 π

, ahol

k

tetszőleges egész szám. Ez tehát a feladat megoldása.

6. Legfeljebb hány különböző pozitív prímszám adható meg úgy, hogy közülük bármely három összege is prímszám legyen?

Megoldás. Némi próbálkozás után találhatunk négy ilyen számot (pl. a 7, 11, 13, 23 vagy 19, 23, 37, 41 számnégyes megfelelő), de ötöt nem sikerül. Megmutatjuk, hogy öt egész szám közül mindig kiválasztható három, melyek összege osztható 3-mal (s mivel összegük 3-nál nagyobb, nem prím).
Az egész számok 3-mal osztva 0, 1 vagy 2 maradékot adnak. Ha azonos maradékosztályból választunk ki három számot, ezek összege osztható lesz 3-mal, így egy-egy maradékosztályból legfeljebb két számot választhatunk ki. Ugyanakkor három különböző maradékú szám összege is osztható 3-mal, ezért csak két maradékosztályból választhatunk ki számokat.
Azt kaptuk, hogy legfeljebb két maradékosztályból, legfeljebb két-két számot, vagyis összesen legfeljebb négy számot választhatunk ki, ha azt akarjuk, hogy közülük semelyik három összege se legyen osztható 3-mal; a feladat feltételeinek megfelelően tehát legfeljebb 4 szám adható meg.

7. Az

R

sugarú gömbbe írt egyenes körhengerek közül melyik henger térfogata maximális? Mekkora a térfogat lehető legnagyobb értéke?

Megoldás. A beírt henger térfogata csak akkor lehet maximális, ha tengelye átmegy a gömb középpontján, s alap- és fedőkörének kerülete a gömb felületén van. Jelöljük a henger alapkörének sugarát

r

-rel, magasságát

m

-mel, s tekintsük a tengelyen átmenő síkmetszetet!

2 R

2 r

m

oldalú derékszögű háromszögből kapjuk a

4 R^{2} = 4 r^{2} + m^{2}

összefüggést, s ezen feltétel mellett kell

V = r^{2} π m

maximumát meghatároznunk.

r^{2}

-et kiküszöbölve

4 V = (4 R^{2} - m^{2}) π m

. Emeljük négyzetre az egyenletet, hogy a számtani-mértani közép közötti egyenlőtlenséget alkalmazni tudjuk. (Szabad négyzetre emelni: a tényezők pozitívak, s

{(4 V)}^{2}

ugyanott lesz maximális, ahol

4 V

\begin{matrix} 16 V^{2} = {(4 R^{2} - m^{2})}^{2} π^{2} m^{2}, \frac{32 V^{2}}{π^{2}} = {(4 R^{2} - m^{2})}^{2} \cdot 2 m^{2} . \end{matrix}

Ha most írjuk föl a

(4 R^{2} - m^{2})

(4 R^{2} - m^{2})

2 m^{2}

pozitív számokra a számtani-mértani közép közötti egyenlőtlenséget, akkor a számtani közép állandó:

\begin{matrix} \sqrt[3]{(4 R^{2} - m^{2}) (4 R^{2} - m^{2}) \cdot 2 m^{2}} \leq \frac{(4 R^{2} - m^{2}) + (4 R^{2} - m^{2}) + 2 m^{2}}{3}, \end{matrix}

(1)

ahonnan

\sqrt[3]{\frac{32 V^{2}}{π^{2}}} \leq \frac{8 R^{2}}{3}

\frac{32 V^{2}}{π^{2}} \leq \frac{512 R^{6}}{27}

V^{2} \leq \frac{16 π^{2} R^{6}}{27}

V \leq \frac{4 π R^{3}}{3 \sqrt[]{3}}

.
A henger térfogata legfeljebb

\frac{4 π R^{3}}{3 \sqrt[]{3}}

lehet (ez a gömb térfogatának

\frac{1}{\sqrt[]{3}}

része). A lehető legnagyobb érték akkor érhető el, ha az (1) egyenlőtlenség jobb oldalán szereplő tagok egyenlőek, vagyis

4 R^{2} - m^{2} = 2 m^{2}

. Mivel

4 R^{2} = 4 r^{2} + m^{2}

, innen

m = \frac{2}{\sqrt[]{3}} R

és

r = \sqrt[]{\frac{2}{3}} R

8. Adott az

y = x^{2}

parabola és az

A (9,8)

pont. A parabola mely

P

pontjába húzott érintőjére igaz, hogy ez az érintő merőleges az

A P

egyenesre?

Megoldás. Legyen a

P

futópont koordinátája

(p; p^{2})

, a

P

pontba húzott érintő meredeksége

m

. Ekkor az érintő egyenlete

e : y - p^{2} = m (x - p)

. Mivel

e

érinti a parabolát, az egyenes és a parabola közös pontjait adó

y = x^{2}

y - p^{2} = m (x - p)

egyenletrendszernek pontosan egy megoldása van. (Az

y

tengellyel párhuzamos egyenest kizártuk.)
Az egyenletrendszerből

x^{2} - m x - p^{2} + p m = 0

egyenlet adódik

x

-re. Egy megoldást akkor kaphatunk, ha a diszkrimináns nulla:

m^{2} + 4 p^{2} - 4 p m = 0

{(m - 2 p)}^{2} = 0

, vagyis

m = 2 p

.
Tehát az

y = x^{2}

parabola tetszőleges

P (p; p^{2})

pontjába húzott érintő meredeksége

2 p

.
Az érintő egy irányvektora

v (1; 2 p)

, ez a feladat szerint merőleges az

\vec{A P}

vektorra.

\vec{A P} = \vec{P} - \vec{A} = (p; p^{2}) - (9; 8) = (p - 9; p^{2} - 8)

. Két vektor merőlegességét legegyszerűbben a skalárszorzatuk segítségével írhatjuk fel:

v \cdot \vec{A P} = 0

\begin{matrix} v \cdot \vec{A P} = (1; 2 p) \cdot (p - 9; p^{2} - 8) = p - 9 + 2 p^{3} - 16 p, \end{matrix}

átrendezés után a

2 p^{3} - 15 p - 9 = 0

harmadfokú egyenletet kapjuk.
Észrevehetjük, hogy

p = 3

gyöke az egyenletnek. A

(p - 3)

gyöktényezőt kiemelve

2 p^{3} - 15 p - 9 = (p - 3) (2 p^{2} + 6 p + 3)

. A

2 p^{2} + 6 p + 3 = 0

egyenlet további gyökei

p_{1} = \frac{- 3 + \sqrt[]{3}}{2}

(\approx - 0, 63)

és

p_{2} = \frac{- 3 - \sqrt[]{3}}{2}

(\approx - 2, 37)

.
Tehát három megfelelő

P

pontot kaptunk:

P_{1} (3; 9)

P_{2} (- 0, 63; 0, 40)

P_{3} (- 2, 37; 6, 00)