Kezdőlap


Cím:	Az elektrosztatikus mező újabb érdekes tulajdonságai
Szerző(k):	Pozsgay Balázs
Füzet:	2001/december, 555 - 559. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az elektrosztatikus mező sok fontos és érdekes tulajdonsággal rendelkezik. Ilyen például a ponttöltés terének gömbszimmetriája, vagy az a tétel, amely szerint egy homogénen töltött gömbhéj tere kívül megegyezik egy ugyanakkora töltésű ponttöltés terével, a belsejében pedig a térerősség nulla. Ezeken a közismert dolgokon kívül felmerült bennem egy kérdés, amelynek sem a megoldását sem magának a problémának a felvetését nem találtam meg egyetlen könyvben sem. Ez a probléma ‐ főleg annak alapos átgondolása után ‐ számomra új oldalról világította meg az elektrosztatikus (és vele együtt a hasonló egyenletekkel leírható magnetosztatikus, illetve gravitációs) erőterek tulajdonságait.

Egy átlagolási probléma

A következő kérdés foglalkoztatott: vajon mit kapunk akkor, ha egy tetszőleges (nem feltétlenül gömbszimmetrikus) elektrosztatikus mezőben gondolatban felveszünk egy gömbfelületet, s erre átlagoljuk az elektromos térerősséget, illetve az elektromos potenciált?

Úgy sejtettem, hogy a térerősség átlaga meg fog egyezni a gömb középpontjában mérhető térerősséggel, a potenciál átlagértéke pedig a középpontbeli potenciállal. Mint látni fogjuk, ez a sejtés teljes általánosságban ugyan nem helyes, de nem áll messze a valóságtól, s kis módosítással egy igaz állítssá lehet átfogalmazni.

A ,,nyers erő'' módszere

Végezzük el a potenciál átlagolását először teljesen mechanikusan, vagyis hívjuk segítségül az integrálszámítást! (Ha az olvasó még járatlan lenne a matematika ezen fejezetében, ne tegye le rögtön a cikket, legfeljebb ugorja át az alábbi részt, mert később elemi megoldást is fog találni a felvetett problémára!)

Tekintsünk először egy olyan erőteret, melyben egyetlen ponttöltés van csak, és

l

távolságban helyezkedik el az

R

sugarú képzeletbeli gömb középpontjától. Az

U

potenciál ,,átlagán'' a

\begin{matrix} U_{átlag} = \frac{\sum_{i}^{} U_{i} \cdot d f_{i}}{\sum_{i}^{} d f_{i}} \end{matrix}

(1)

mennyiséget értjük. Ennek értelmezése: a gömbfelszínt felbontjuk elég kicsi

d f_{i}

felületelemekre (

i

a felületdarabkák sorszámozására alkalmasan választott index), majd képezzük a felületen mérhető potenciáloknak a felületdarabkák nagysága szerint súlyozott átlagát. (Hangsúlyoznunk kell, hogy

d f_{i}

a felületdarabka nagysága, tehát skalár mennyiség, ne tévesszük össze a fluxus számításánál használatos ,,irányított felületelem'' vektorral.)

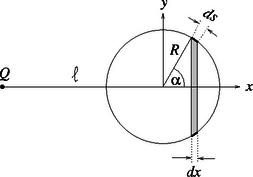Álljunk neki a számolásnak! Vegyük fel a koordináta-rendszerünket az ábrán látható módon: a ponttöltés kerüljön az

x

tengelyre, a gömb középpontja pedig legyen az origóban. Bontsuk fel a gömb felszínét

d x

széles gömbövekre. Első dolgunk ezek felületének meghatározása:

\begin{matrix} d f = 2 π y \cdot d s = 2 π R sin α \cdot \frac{d x}{sin α} = 2 π R \cdot d x . \end{matrix}

Azt kaptuk tehát, hogy a gömbövek felülete csak

d x

-től függ, s ez nagyon kényelmessé teszi további dolgunkat. A fenti képlet alapján pl. könnyen meg tudjuk mondani a gömb teljes felszínét:

\begin{matrix} F = \sum d f = 2 π R \cdot \sum_{x = - R}^{+ R} d x = 2 π R \cdot 2 R = 4 π R^{2} . \end{matrix}

(2)

Következő lépésben kiszámoljuk a potenciált a gömbfelszín

x

koordinátájú helyein.

\begin{matrix} U = \frac{k Q}{r}, \end{matrix}

ahol

\begin{matrix} r = \sqrt[]{{(l + x)}^{2} + y^{2}} = \sqrt[]{{(l + x)}^{2} + R^{2} - x^{2}} = \sqrt[]{l^{2} + 2 l x + R^{2}} . \end{matrix}

Most rátérhetünk magára az integrálásra. Mivel a ponttöltéstől azonos távolságra levő felületdarabkák egy keskeny gömböv mentén helyezkednek el, érdemes a gömbfelületek ilyen ,,övekre'' darabolni, s ezek szerint végezni az átlagolást:

\begin{matrix} U_{átlag} & = & \frac{1}{F} \int U \cdot d f = \frac{1}{4 π R^{2}} 2 R π \cdot k Q \cdot \int_{- R}^{R} \frac{1}{\sqrt[]{ℓ^{2} + 2 ℓ x + R^{2}}} d x = & (3) \\ = & \frac{k Q}{2 ℓ R} (| ℓ + R | - | ℓ - R |) = {\begin{matrix} \frac{k Q}{ℓ}, & haℓ \geq R, \\ \frac{k Q}{R}, & haℓ \leq R . \end{matrix} \end{matrix}

Furcsa képletet kaptunk. Egyrészt érdekes az alakja, hiszen a végső formulában

R

és

l

közül vagy csak az egyik, vagy csak a másik mennyiség szerepel, méghozzá teljesen szimmetrikus módon. Furcsa a kapott formula fizikai szempontból is, hiszen ezek a képletek írják le, hogy mennyi egy

Q

töltésű, homogén töltéseloszlású gömbhéj potenciálja a középponttól

l

távolságban. Ez ugyan látszólag egy egészen más probléma, mint amit eddig vizsgáltunk, de ‐ mint látni fogjuk ‐ a kettő között szoros (és jól kihasználható) kapcsolat van.

Elemi megoldás az energiaviszonyok tanulmányozásából

Gondoljuk most azt, hogy az eddig képzeletbeli (nevezhetjük ,,virtuálisnak'' is) gömbhéjunk egy valóságos, létező (szigetelő) test, amelyet egyenletesen feltöltöttünk, méghozzá éppen egységnyi,

q = 1

nagyságú töltéssel. Vajon mekkora ennek a homogénen töltött gömbhéjnak és a középpontjátó

l

távolságra levő

Q

nagyságú ponttöltésnek a kölcsönhatási energiája?

Ezt az energiát kétféle módon is meghatározhatjuk: egyrészt úgy, hogy a gömbhéj potenciálját kiszámítjuk a ponttöltésünk helyén (ezt könnyen megtehetjük, hiszen a töltéseloszlás gömbszimmetrikus), majd ezt a potenciált megszorozzuk a ponttöltés nagyságával (

Q

-val). Az eredmény közismert, éppen a (3) formula végén megadott kifejezés.

Másképp is eljárhatunk: a pontszerű

Q

töltés éltal létrehozott gömbszimmetrikus (Coulomb-féle) erőtérben számoljuk ki a gömbhéjon egyenletesen elosztott töltés potenciális energiáját. Ez utóbbit elvben úgy tehetjük meg, hogy a gömbhéjat gondolatban kicsiny darabkákra bontjuk, az egyes (

d f

nagyságú) felületdarabkákra eső töltés nagyságát, vagyis

d f / (4 π R^{2})

-t megszorozzuk a

Q

töltés által a felületdarabka helyén létrehozott potenciállal, majd ezeket az energiákat összeadogatjuk.

A másik számítási módszer technikailag sokkal bonyolultabb, mint az első. Szerencsére nem kell végigszámolnunk a bonyolult összegzést, hiszen az eredménye nyilvánvalóan ugyanannyi, mint az első számolásé.

Vegyük észre, hogy a második számolási módszerrel adódó mennyiség nem más, mint a

Q

töltés által létrehozott potenciál átlaga az

R

sugarú gömb felületén. A két számítás eredményének egyenlőségét kihasználva tehát meg tudtuk határozni ‐ méghozzá elemi úton, integrálszámítás alkalmazása nélkül ‐ a kérdéses átlagértéket:

\begin{matrix} U_{átlag} = {\begin{matrix} \frac{k Q}{ℓ}, & haℓ \geq R, \\ \frac{k Q}{R}, & haℓ \leq R. \end{matrix} \end{matrix}

(4)

Az elektromos térerősség átlaga

Következő feladatunk a térerősség átlagolása lesz. Ezt az eredményeink alapján kétféleképpen is megtehetjük. Az első módszer azon az észrevételen alapul, hogy a térerősség szoros kapcsolatban van a potenciállal, pontosabban annak térbeli változási ütemével. Ezt a kapcsolatot úgy fogalmazhatjuk meg matematikai alakban, hogy ha egy

\vec{E}

elektromos térerősségű helyről egy kicsiny

Δ \vec{x}

elmozdulás-vektornyival odébbmegyünk, akkor az elektromos potenciál megváltozása:

\begin{matrix} Δ U = - \vec{E} \cdot \vec{Δ x} . \end{matrix}

(5)

(A fenti képletben a két vektor közötti pont a skalárszorzat műveletét jelenti, a negatív előjel pedig azt veszi figyelembe, hogy

\vec{E}

irányába haladva a potenciális energia csökken.)

Ezek szerint ha egy elektrosztatikus erőtérben helyről helyre ismerjük a potenciált, abból már az (5) alapján a térerősséget is kiszámíthatjuk. Egy adott helyen a térerősség komponenseit úgy határozhatjuk meeg, hogy a kérdéses helyről indulva a koordináta-tengelyek mentén sorra elmozdulunk egy kicsiny

Δ s

távolságnyit, majd a potenciálváltozásokat elosztjuk

Δ s

-sel. Az így kapott három mennyiség (az előjeltől eltekintve) éppen a térerősség három komponense lesz.

Mi most nem egy adott pontbeli térerősséget, hanem a térerősség átlagát szeretnénk meghatározni. Mivel azonban a térerősség átlagának komponensei nyilván a komponensek átlagaival egyeznek meg, ezek pedig az egész gömbfelület elmozdításakor bekövetkező energia-változással fejezhetők ki, a (4) és (5) képletek segítségével célhoz érhetünk. Az

x

irányú térerősség-komponens átlagát például úgy számíthatjuk ki, hogy az egész gömbfelszínünket elmozdítjuk

x

irányba

Δ s

-sel. (Kihasználtuk, hogy a potenciálváltozások átlaga megegyezik az átlag változásával.)

Nézzük meg konkrétan, mit mond a (4)-es képlet és a fenti eljárás a térerősség átlagáról. Ha a ponttöltés a gömbfelületen belül van, akkor hiába mozgatjuk a gömbfelszínt, a potenciál átlaga nem fog változni, hiszen az csak

R

-től függ,

l

-től nem! Emiatt a térerősségnek a gömb felületére vett étlaga nulla. Ha a

Q

töltés a gömbön kívül van, akkor a helyzet kicsit bonyolultabb. Ilyenkor viszont azt a tényt használhatjuk ki, hogy a potenciál átlaga nem függ

R

-től, vagyis a gömbünk lehetne akár ,,pontszerű'' is. No de ha eyz lenne a helyzet, akkor a potenciális energia két ponttöltés ismert kölcsönhatási energiájával egyezne meg, a potenciális megváltozásból számolt térerősség pedig éppen a

Q

töltés által a gömb középpontjában létrehozott Coulomb-mező térerősségével lenne egyenlő. Összefoglalva: egy pontszerű töltés elektromos térerősségének gömbfelületi átlagát a következő képlet adja meg:

\begin{matrix} {\vec{E}}_{átlag} = {\begin{matrix} \frac{k Q}{ℓ^{2}} \cdot \frac{\vec{ℓ}}{ℓ}, & haℓ > R, \\ 0, & haℓ < R. \end{matrix} \end{matrix}

(6)

Szuperpozíció

Mindeddig egyetlen pontszerű töltéssel, annak elektrosztatikus terének valamilyen képzeletbeli gömbfelületre vett átlagával foglalkoztunk. mi a helyzet akkor, ha nem egy, hanem sok ponttöltés együttese (vagy akár töltések folytonos eloszlása) hozza létre az elektrosztatikus mezőt. Az eredő elektromos térerősség az egyes pontszerű töltésdarabkák terének vektori összege (szuperpozíciója), az összeg átlaga pedig az egyes térerősség-összetevők átlagának összege.

Az előző pontban beláttuk, hogy ‐ pontszerű forrás esetén ‐ az átlagos térerősség megegyezik a gömb középpontjában mérhető térerősséggel. A szuperpozíció elvének alkalmazásával abből rögtön következik, hogy az eredő térerősség átlaga egy tetszőlegesen bonyolult elektrosztatikus mező esetében is éppen a gömbön kívül található töltések által a gömb középpontjában létrehozott elektromos térerősséggel egyezik meg. A gömbön belül található töltések terét nem szabad figyelembe vennünk, azok nem adnak járulékot az átlagos térerősséghez! Ez a kis ,,apróság'' az, amit a tételünk első, sejtésen alapuló megfogalmazása még nem tartalmazott. Érdekes, hogy az irányított (vektornak tekintett) felületdarabkák szerinti összegzésnél (átlagolásnál) éppen fordított a helyzet: a gömbön kívül levő töltések járuléka nulla, csak a belül elhelyezkedő töltések kapnak szerepet, ezek határozzák meg a felületen áthaladó elektromos fluxust.

Hatás‐ellenhatás

Befejezésként megmutatjuk, hogy az elektromos térerősség gömbfelületi átlagára vonatkozó eredményt egyszerűbb módon, a potenciálra való hivatkkozáss nélkül is megkapjuk, méghozzá rögtön a legáltalánosabb, mindenféle szimmetriát nélkülöző mezőkre.

Gondoljuk ismét azt, hogy van egy ténylegesen létező, egyenletesen feltöltött gömbfelületünk egységnyi össztöltéssel. Ilyenkor a térerősség átlaga éppen azzal az erővel egyenlő, amelyet a teljes töltésrendszer a gömbfelületre kifejt. Ez az erő azonban ‐ a hatás-ellenhatás törvénye szerint ‐ a gömbfelület elektrosztatikus terének a többi töltésre kifejtett erőhatásával, pontosabban annak ellentettjével egyezik meg. Mivel a gömbfelület egyenletesen töltött, az erőtere megegyezik egy ponttöltés terével (legalábbis a gömbön kívül), az általa kifejtett erő tehát egy egységnyi nagyságú pontszerű töltés által a gömbön kívüli töltésekre kifejtett erővel egyenlő.

Alkalmazzuk most ismét a hatás-ellenhatás elvét: a gömbön kívüli töltésekre ható eredő erő (egy előjeltől eltekintve) a gömb középpontjába helyezett egységnyi töltésre ható erővel egyenlő, ez pedig nem más, mint a külső töltések elektromos térerőssége a gömb középpontjában. Mi a helyzet a gömbön belül található töltésekkel? Ennek végiggondolását az Olvasóra bízzuk.

Megfontolásaink során az elektrosztatikus mezőnek csupán azt a tulajdonságát használtuk ki, hogy pontszerű forrás terének nagysága a távolság négyzetével fordítottan arányos, továbbá azt, hogy érvényes a szuperpozíció elve. Ezekkel a tulajdonságokkal a Newton-féle gravitációs mező is rendelkezik, és némi megfontolás után a magnetosztatikus mezőre is átvihető. (Mágneses töltés ugyan nem található a Természetben, de a magnetosztatikus mező úgy írható le, mintha léteznének különálló mágneses pólusok, s rájuk az elektrosztatikához hasonló törvények teljesülnének.) Emiatt a cikkünkben tárgyalt valamennyi állítás változatlan formában érvényes a gravitációs, illetve a magnetosztatikus mezőkre is, sőt, a majdan felfedezendő egyéb ,,Coulomb-szerű'' vektorterekre is alkalmazható.

\begin{matrix} Pozsgay Balázs(ELTE, I. éves fizikus hallgató) \end{matrix}