Kezdőlap


Cím:	A 32. Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):	Gnädig Péter , Vankó Péter
Füzet:	2001/november, 493 - 502. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kísérleti forduló ¹

Forgó folyadék

1. rész:

g

Meghatározása forgó folyadék segítségével
Tekintsük a forgó folyadéknak egy kicsiny, meghatározott

m

tömegű, folyadék felszínén elhelyezkedő ,,darabkáját'', és írjuk fel ezen folyadékmennyiség mozgásegyenletét! A kiszemelt anyagdarabkára a függőleges

m g

gravitációs erő és a környező folyadék által a felületre merőlegesen kifejtett ereje hat. Ezen két erő eredője vízszintes kell legyen (hiszen a folyadékdarabka vízszintes síkban

x

sugarú körpályán mozog), s az eredő nagysága ─ Newton II. törvénye értelmében ─

m x ω^{2}

. Az 1. ábráról leolvashatjuk, hogy a folyadék felszínének meredekségét valóban a megadott

tg θ = ω^{2} x / g

összefüggés adja meg.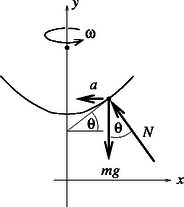

1. ábra.

A feladat útmutatásait követve ─ a geometriai távolságokat vonalzóval, a forgás szögsebességét stopper segítségével mérve ─ függőlegesen beeső lézersugár visszaverődéséből a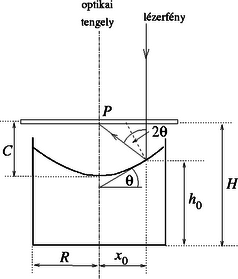

\begin{matrix} tg 2 θ = \frac{x_{0}}{H - h_{0}} = \frac{R}{\sqrt[]{2} (H - h_{0})} \end{matrix}

összefüggésnek megfelelően (2. ábra) meghatározhatjuk különbőző

ω

-k esetén a

θ

szöget. (Erre a részfeladatra csak az a versenyző kaphatott maximális pontszámot, aki legalább 6 ,,kellően különböző'' szögsebességnél mért, és mindegyik ─ már stabilizálódott ─ forgásnál úgy járt el, hogy a kisebb szögsebességeknél legalább 10, gyorsabb forgásnál pedig legalább 15‐20 körülfordulás idejéből számította ki a szögsebességet.) Ha a mért geometriai adatokból kiszámított

tg θ

-t a szögsebesség négyzetének függvényében ábrázoljuk, és a kapott (becsült mérési hibákat is feltüntető) ,,pontokra'' egyenest illesztünk, akkor ennek az egyenesnek a meredeksége a megadott képlet szerint (egy arányossági tényezőtől eltekintve) éppen a nehézségi gyorsulás mért értékét szolgáltatja. Az illesztett egyenes meredekségének (akár szabad szemmel leolvasható, akár az egyes pontok pontatlanságából zsebszámológéppel kiszámítható) bizonytalansága megadja

g

mérési hibájának nagyságrendjét is. A rendelkezésre álló eszközökkel kapható tipikus mérési eredmény:

g = 980 \pm 30 {cm/s}^{2}

2. ábra.

2. rész: Optikai rendszer

a)

A fókusztávolság vizsgálata
Az ernyőt meghatározott

H

magasságban tartva a motor fordulatszámát óvatosan növelve megkereshető az a szögsebesség, amely mellett a (függőleges) optikai tengellyel párhuzamosan beeső lézerfény visszaverődve éppen az optikai tengelynél metszi az ernyőt. A leképező rendszer

C

fókusztávolsága jó közelítéssel

(H - h_{0})

-nak vehető (hiszen a folyadék ,,behorpadása'' általában elhanyagolhatóan kicsiny a fókusztávolság mellett). A mérési adatok szerint a fókusztávolság és a szögsebesség közötti kapcsolat

C \propto ω^{- 2}

jellegű. Ezt a sejtést empirikusan úgy igazolhatjuk, hogy

1 / C

-t

ω^{2}

függvényében ábrázoljuk, és megnézzük, milyen pontossággal illeszthető a mérési adatokra egyenes.
Az adatok kiértékelését úgy is elvégezhetjük, hogy a folyadéktükör

f

fókusztávolsága és az

ω

szögsebesség közötti kapcsolatot

f = A \cdot ω^{n}

alakban keressük, ahol

A

és

n

meghatározandó állandók. A mérési adatokból kiszámítható

log f

-t ábrázolhatjuk

log ω

függvényében, s ha valóban a feltételezett kapcsolat áll fenn

f

és

ω

között, akkor egy

n

meredekségű egyenest várhatunk. Az ilyen módon kiértékelt adatokból

n

(meglehetősen nagy bizonytalansággal)

- 1, 7

körüli értéknek adódott. (A versenyen a

- 2 < n < - 1, 6

tartományba eső értékeket fogadták el reális mérési eredményként.)
Megjegyzés. A fókusztávolság és a szögsebesség közötti kapcsolat elméleti megfontolásokkal is alátámasztható. A forgó folyadék felszínét jellemző

y = y_{0} + x^{2} / (4 C)

egyenletet differenciálva és az

y' = tg θ = (x / g) ω^{2}

képlettel egybevetve leolvashatjuk, hogy

1 / C

valóban arányos

ω^{2}

-tel, s az arányossági tényező

2 / g

.
Ugyanehhez az eredményhez differenciálszámítás nélkül is eljuthatunk, ha meggondoljuk, hogy a forgó folyadékhoz rögzített koordináta-rendszerben a folyadék minden része, így a felszínén lévő ,,darabkái'' is egyensúlyban vannak. A felszínen (a forgástengelytől

x

távolságban, az edény aljától pedig

y

magasságban) levő

m

tömegű anyagdarabka

m g y

gravitációs helyzeti energiával, a

D = - m ω^{2}

,,rugóállandóval'' jellemezhető ,,centrifugális erőtérben'' pedig

D x^{2} / 2 = - m ω^{2} x^{2} / 2

potenciális energiával rendelkezik. Egyensúlyi állapotban a folyadék felszíne ekvipotenciális, a felület mentén a folyadékdarabkák összenergiája mindenhol ugyanakkora:

\begin{matrix} m g y - \frac{1}{2} m ω^{2} x^{2} = konstans, \end{matrix}

azaz

\begin{matrix} y = \frac{ω^{2} x^{2}}{2 g} + y_{0} . \end{matrix}

Ezt a kifejezést a parabola fókusztávolságot is tartalmazó egyenletével összevetve megkapjuk, hogy

1 / C = 2 ω^{2} / g .

A fenti elméleti megfontolások nem képezték a mérési feladat részét, levezetésüket nem várták el a versenyzőktől.

b)

Az ernyőn látható ,,kép'' analízise
A lézer fejére erősíthető betét egy rövid fókusztávolságú kicsiny lencsét tartalmazott, amely a lézer párhuzamos fénysugarait széles szögtartományban szétszórta. A szétfutó fény útjába (még a betétrész belsejében) egy jellegzetes alakban (pl. félhold formájában) kivágott árnyékvető lemezkét helyeztek, így az áttetsző papírra (ernyőre) eső lézerfény megjelenítette az árnyékvető lemezke alakját. Ez a megjelenítés azonban különbözik az optikai leképező rendszerek szokásos képalkotásától, erre utalt a ,,kép'' szónál az idézőjel. A fényforrásból széttartóan kiinduló sugarak nem az ernyőnél metszik egymást, ott tehát nem az optikai képalkotás törvényeinek megfelelő képet, hanem csupán árnyékjelenséget látunk. A forgó folyadék parabolatükre magát a fényforrást (és az árnyékvető betétrészt) képezi le, s az ernyőn kialakuló árnyékkép olyan lesz, mintha a lézer nem az eredeti helyén, hanem a leképezett helyzetében lenne.
Az ernyőn megjelenő ,,direkt árnyékkép'', illetve a forgó folyadékról visszavert árnyékkép állását és nagyságát tekintve is különbözhet. Az álló folyadék felszíne síktükörként viselkedik, ilyenkor az ernyőn látszó tükrözött árnyékkép a direkt árnyékképpel egyező állású, de annál nagyobb méretű (3.a ábra). Az igazi (a sugarak metszéspontjában képződő) optikai kép virtuális (és nem az ernyőn keletkezik).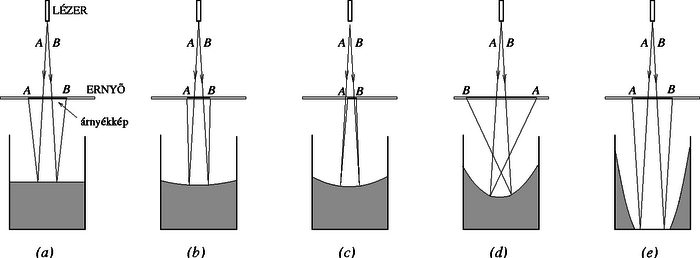

3. ábra.

A szögsebességet lassan növelve a fókusztávolság csökken, a lézerfej optikai képe egyre messzebb kerül (de továbbra is virtuális). A tükröződött árnyékkép mérete a szögsebesség növekedtével egyre csökken, állása a direkt árnyékképpel megegyező (3.b ábra). Hasonló a helyzet akkor is, amikor a folyadék fordulatszáma már olyan nagy, hogy a lézer feje a fókuszponton belülre kerül (3.c ábra): a visszavert árnyékkép mérete egyre csökken, állása a direkt árnyékéval megegyező, de a lézer optikai képe már valódi kép lesz.
A fordulatszámot tovább növelve a lézerfej optikai képe az ernyő alá fog kerülni (3.d ábra). Ekkor a visszavert árnyékkép állása megfordul, a direkt árnyékkal ellentétes állású lesz, és a mérete a szögsebesség növekvő függvénye. A lézerfej optikai képe továbbra is valódi kép.
A fordulatszámot még tovább növelve ez a tendencia is megváltozik, hiszen egy bizonyos (az edényben levő folyadék mennyiségétől függő) kritikus értéknél a folyadék felszíne eléri az edény alját. A kritikus fordulatszámot számottevően meghaladó fordulatszámoknál a lézer fénye már nem a folyadékról, hanem a sík fenéklapról verődik vissza (3.e ábra). Ebben tartományban az árnyékkép ismét egyenes állású lesz, az optikai kép virtuális, és az árnyékkép mértéke nyilvánvalóan nem függ a szögsebességtől.

3. rész: A törésmutató

Az optikai rács (és a megadott elhajlási képlet) segítségével a lézerfény hullámhossza levegőben könnyen mérhető. A lézerfényt célszerű merőlegesen ejteni a rácsra, majd egy mérhető távolságra levő ernyőn megmérhetjük az elhajlási maximumok távolságát, s kiszámíthatjuk az elhajlási szögeket is. A mérés pontosságát növeli, ha több (a verseny rendezőinek elvárása szerint legalább három) elhajlási maximumból számítjuk ki a hullámhosszat. A hullámhossz mérését az elfogadható hibabecslés teszi teljessé.
Az előző mérést folyadékba merített diffrakciós ráccsal megismételve meghatározhatjuk a fény hullámhosszát a folyadékban. Ennek a hullámhossznak és a levegőben mért hullámhossznak az aránya éppen a folyadéknak (levegőre vonatkoztatott)

n

törésmutatójával, vagyis a mérendő mennyiséggel egyezik meg.

Elméleti forduló

1. feladat. Négy (egymástól független) probléma.

A. Klisztron

a)

- e

töltésű,

m

tömegű,

v_{0}

kezdősebességű elektronok

m v_{0}^{2} / 2

mozgási energiája

\pm V

feszültség hatására

\mp e V

értékkel változik meg. Így a bal oldali üregből kilépő felgyorsított részecskék sebessége

\begin{matrix} v_{+} = \sqrt[]{v_{0}^{2} + 2 (\frac{e}{m}) V} = 2, 044 \cdot 10^{6} \frac{m}{s}, \end{matrix}

a lelassított elektronoké pedig

\begin{matrix} v_{-} = \sqrt[]{v_{0}^{2} - 2 (\frac{e}{m}) V} = 1, 956 \cdot 10^{6} \frac{m}{s} . \end{matrix}

A 4. ábra az elektronsugár egyes részecskéinek vázlatos út‐idő diagramját mutatja. Erről leolvasható, hogy a két üreg közötti

b

távolság akkor esik éppen az első torlódási helyre, ha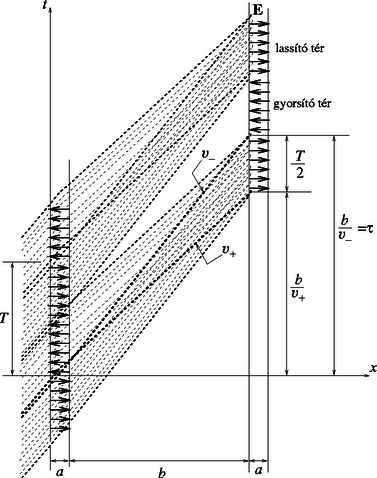

\begin{matrix} \frac{b}{v_{+}} + \frac{T}{2} = \frac{b}{v_{-}}, \end{matrix}

azaz

\begin{matrix} b = \frac{T}{2} \frac{v_{+} v_{-}}{v_{+} - v_{-}} = 2, 272 cm . \end{matrix}

4. ábra.

b)

A 4. ábrán az elektromos térerősség irányát is feltüntettük a bal oldali üreg (

x \approx 0

) és a jobb oldali üreg (

x \approx b

) helyén. A periodikusan (négyszögjelnek megfelelően) váltakozó, de egymáshoz képest

τ

időkülönbséggel, azaz

Δ φ = 2 π \cdot τ / T

fáziskülönbséggel eltolt jelek akkor fogják a kilépő elektronokat fékezni, ha a torlódási helyen a térerősség jobbra mutat. Ennek feltétele az, hogy

b = v_{-} τ,

azaz

\begin{matrix} Δ φ = 2 π \cdot \frac{b}{T v_{-}} = 2 π \cdot \frac{v_{+}}{v_{+} - v_{-}} = 2 π \cdot 11, 613. \end{matrix}

Tekintettel arra, hogy egy periodikus függvény fázisának eltolása csak

2 π

egész számú többszöröse erejéig határozott, a fenti szám egész részét elhagyhatjuk:

\begin{matrix} Δ φ = 0, 613 \cdot 2 π radián = 220^{\circ}, \end{matrix}

vagy ami ezzel egyenértékű:

Δ φ = - 140^{\circ}

B. Molekulák közötti távolság
Az ideális gáznak tekintett vízgőz sűrűsége a gáztörvény szerint

\begin{matrix} ϱ_{V} = \frac{m}{V} = \frac{M p_{0}}{R T} . \end{matrix}

A víz és a gőz sűrűségének aránya légköri nyomáson és a forráspont hőmérsékletén

\begin{matrix} \frac{ϱ_{L}}{ϱ_{V}} = \frac{R T ϱ_{L}}{M p_{0}} \approx 1720 \approx 12^{3} . \end{matrix}

Mivel a sűrűsége a molekulák közötti átlagos távolság köbével fordítottan arányos, megállapíthatjuk, hogy gőzfázisban a molekulák kb. 12-szer messzebb vannak egymástól, mint folyadék halmazállapotban.

C. Egyszerű fűrészfog-generátor

a)

A kapcsoló zárását követően a kondenzátor az

R

ellenálláson keresztül eleinte gyorsan, majd egyre lassabban töltődik. A

V_{0}

feszültség és a telepfeszültség különbsége az idő exponenciális függvénye szerint csökken mindaddig, míg

V_{0}

el nem éri a

V_{f}

kisülési feszültséget. Ekkor a szikrakisülés hatására

V_{0}

hirtelen nullára csökken, majd a folyamat kezdődik elölről. (5.a ábra).

b)

V_{f} ≪ V_{i}

esetén a kondenzátor feszültsége elhanyagolható a telepfeszültség mellett. A töltőáram ilyenkor jó közelítéssel állandónak tekinthető, a kondenzátor feszültsége tehát (egészen a szikrakisülésig) időben lineárisan növekszik (5.b ábra).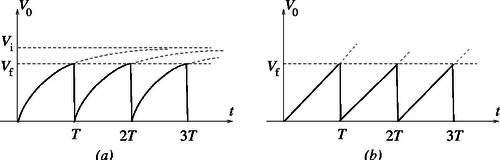

5. ábra.

c)

Ha a linearitási feltétel teljesül, az áramerősség

I = V_{i} / R

, a kondenzátor töltése

t

időtartamú töltés után

Q = I t

, feszültsége pedig

\begin{matrix} U = \frac{Q}{C} = \frac{V_{i}}{R C} t . \end{matrix}

Ez akkor egyezik meg a

V_{f}

kisülési feszültséggel, amikor

\begin{matrix} t = T = \frac{V_{f}}{V_{i}} R C, \end{matrix}

ekkora tehát a fűrészfog-generátor periódusideje.

Megjegyzés. A periódusidőt megadó formulát a kondenzátor töltődését leíró

\begin{matrix} V_{f} = V_{i} (1 - e^{- T / (R C)}) \end{matrix}

összefüggésből is megkaphatjuk, ha kihasználjuk, hogy

V_{f} ≪ V_{i}

, emiatt

T ≪ R C

. Az exponenciális függvény kis

x

-ekre érvényes

e^{x} \approx 1 + x

közelítő alakjából

\begin{matrix} V_{f} \approx V_{i} [1 - (1 - \frac{T}{R C})] = \frac{V_{i} T}{R C}, ahonnan T \approx \frac{V_{f}}{V_{i}} R C . \end{matrix}

d)

R

ellenállás értékét megváltoztatva (és a szikraköz

V_{f}

kisülési feszültségét rögzített értéken tartva) fűrészfogjelnek csak a periódusideje változik, amplitúdója nem.

e)

Ha az ellenállás nagyságát és a szikraköz távolságát egyszerre változtatjuk, méghozzá olymódon, hogy az

R \cdot V_{f}

szorzat változatlan maradjon, akkor a fűrészfogjelnek csak az amplitúdója változik, periódusideje nem.

f)

A megadott (,,fordított fűrészfog'') jelalak többféle kapcsolással is megvalósítható. Egy lehetséges megoldást mutat a 6. ábra.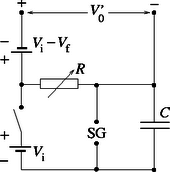

6. ábra.

D. Atomsugár

I. (hivatalos) megoldás:

T

hőmérsékletű gázban az

M

tömegű atomok átlagsebessége az energia egyenletes eloszlásának tételéből (az ekvipartíciós tételből) határozhatjuk meg. Eszerint

\begin{matrix} \frac{1}{2} M v^{2} = \frac{1}{2} k T, \end{matrix}

ahol

v

a sebesség valamelyik komponensének átlagos nagysága,

k

pedig a Boltzmann-állandó. (Az ,,átlagos nagyság'' a négyzetes átlagolást, a sebességkomponens négyzetének átlagából vont négyzetgyököt jelenti.) Innen a sebesség bármelyik komponensének, speciálisan a vízszintes összetevőjének átlagos nagysága

v = \sqrt[]{k T / M} .

A kemence falán levő kicsiny lyukon keresztül ,,vízszintesen'' kilépő atomokból álló részecskenyaláb a haladási irányára merőlegesen fokozatosan kiszélesedik, az atomsugár átmérője megnő. Ennek az az (egyik) oka, hogy a

D

átmérőjű lyukon áthaladó részecskék

v_{⊥}

,,transzverzális'' (a haladási irányra merőleges) sebessége nem lehet pontosan nulla, hanem a Heisenberg-féle határozatlansági reláció értelmében legalább

\begin{matrix} Δ v_{⊥} \approx \frac{ℏ}{M D} \end{matrix}

nagyságú (ahol

ℏ

2 π

-vel osztott Planck-állandót jelöli).
A atomsugár

t = L / v

idő alatt tesz meg

L

hosszúságú utat, ezalatt

2 v_{⊥} \cdot t

értékkel nő az átmérője, mérete tehát hozzávetőlegesen

\begin{matrix} D_{új} = D + \frac{2 L ℏ}{D \sqrt[]{k T M}} \end{matrix}

lesz. (Ez a kifejezés csak nagyságrendi becslésnek tekinthető, a benne szereplő számfaktort tehát nem szabad nagyon ,,komolyan venni''; a kétszerese, vagy a fele éppúgy elfogadható lenne.)

II. megoldás (Varjú Péter dolgozata alapján). A kemencéből kilépő

v \approx \sqrt[]{k T / M}

sebességű részecskék a de Broglie-féle hipotézis szerint

λ = h / (M v)

hullámhosszúságú ,,anyaghullámnak'' tekinthetők. Ezek az anyaghullámok ─ a fényhullámokhoz hasonlóan ─ elhajlást szenvednek a

D

átmérőjű kör alakú nyíláson. A nyílás különböző részeiből kiinduló hullámok interferálnak, s bizonyos irányokban haladva erősítik, más irányokban viszont kioltják egymást. (Pl. a pontosan ,,előrefelé'' haladó hullámok útkülönbsége nulla, ezek tehát mind erősítik egymást.) Az atomnyaláb szélességét az első interferencia-minimummal azonosítva nagyságrendi becslést kaphatunk az atomsugár kiszélesedésére.
Ismeretes, hogy egy

D

szélességű (párhuzamos falú) rés esetén az első kioltás olyan

θ

elhajlási szögnél észlelhető, amelynél a rés egyik szélétől induló hullámok éppen egy hullámhosszal nagyobb utat tesznek meg az észlelő ernyőig, mint a rés másik szélétől induló hullámok. Ennek geometriai feltétele (kicsiny szögű elhajlások és viszonylag távoli ernyő esetén):

\begin{matrix} sin θ \approx θ = \frac{λ}{D} \approx \frac{h}{D \sqrt[]{k T M}} . \end{matrix}

Jelen esetben az elhajlás nem résen, hanem kör alakú lyukon történik, emiatt a formulában szereplő számfaktor egy kicsit más lesz, ez azonban egy nagyságrendi becslésnél figyelmen kívül hagyható.
A

θ

szögben elhajló atomsugarak az

L

távolságban levő ernyőt

2 L θ

átmérőjű körben érik, ekkora lesz tehát (nagyságrendileg) a kiszélesedett sugár mérete. Ez az érték viszonylag távoli ernyőnél (

L θ ≫ D

teljesülése esetén) megegyezik az előző megoldásban kapott kifejezéssel.

Megjegyzés. A feladat megoldásánál feltételeztük, hogy a kemence falán levő (az atomok méretével összemérhető átmérőjű) lyukon áthaladó atomok egymással nem ütköznek (vagyis a részecskék szabad úthossza sokkal nagyobb, mint a fal vastagsága). Feltettük továbbá azt is, hogy a kemence falának és az atomsugárnak a kölcsönhatása csak a nyaláb transzverzális méretének korlátozásában játszik szerepet, s nem lép fel a klasszikus tömegpontok (pl. biliárdgolyók) rugalmas falak közötti ide-oda pattogásának megfelelő jelenség. Azt is feltételeztük, hogy a részecskék a kilépésük után már szabadon mozognak, a levegő molekuláival nem ütköznek.
Mindezek a feltevések meglehetősen idealisztikusak, kísérleti megvalósításuk szinte lehetetlen. Reálisabb lenne a feladat, ha a kemencéből kilépő részecskék vákuumban haladnának, s a mozgásirányuk bizonytalanságát egy bizonyos távolságban elhelyezett akadályon levő

D

átmérőjű diafragma korlátozná. (G. P.)

2. feladat. Kettőscsillag

a)

Egy

R

sugarú,

T

hőmérsékletű (abszolút fekete) test egységnyi idő alatt

4 π R^{2} σ T^{4}

energiát sugároz ki (

σ

a Stefan‐Boltzmann törvényben szereplő állandó). Ebből az energiából az

ℓ

távolságra levő Földre felületegységenként és időegységenként

\begin{matrix} P = \frac{4 π R^{2} σ T^{4}}{4 π ℓ^{2}} \end{matrix}

(1)

energia jut; ez az egyik mérhető adat.
A kalcium színképvonalának (ugyancsak mérhető)

Δ λ

eltolódása és a csillag

m_{0}

tömege, valamint

R

sugara között az energia-megmaradás törvénye teremt kapcsolatot:

\begin{matrix} \frac{h c}{λ_{0}} - \frac{G m_{0}}{R} \cdot \frac{h}{c λ_{0}} = \frac{h c}{λ} - \frac{G m_{0}}{ℓ} \cdot \frac{h}{c λ} . \end{matrix}

A jobb oldal második tagja

ℓ ≫ R

miatt elhanyagolható. A fenti képletből a közönséges csillag sugarának és tömegének arányára (

Δ λ = λ - λ_{0} ≪ λ_{0}

felhasználásával)

\begin{matrix} \frac{R}{m_{0}} = \frac{G λ_{0}}{c^{2} Δ λ} \end{matrix}

(2)

adódik.
Tudjuk továbbá, hogy a kettőscsillag egyes tagjainak pályasugara

r_{1} = ℓ Δ θ / 2

, illetve

r_{2} = ℓ Δ ϕ / 2

, a szögsebességük kifejezhető a mérhető

2 τ

keringési idővel (

ω = π / τ

), így a neutroncsillagra vonatkozó Newton-féle mozgásegyenlet:

\begin{matrix} \frac{G M m_{0}}{{(r_{1} + r_{2})}^{2}} = M r_{2} ω^{2} . \end{matrix}

(3)

Az (1), (2) és (3) egyenletek összevetéséből a Föld és a kettőscsillag távolságára végül a következő kifejezés adódik:

\begin{matrix} ℓ = \frac{2}{π} \cdot \frac{c τ}{T (Δ θ + Δ ϕ)} \sqrt[]{\frac{2 \cdot Δ λ \cdot \sqrt[]{P / σ}}{Δ ϕ \cdot λ_{0}}} . \end{matrix}

b)

A kibocsátott gáz mozgását a neutroncsillag centrális gravitációs erőtere határozza meg, emiatt a gáz perdülete megmarad:

\begin{matrix} r_{0}^{2} ω_{0} = r_{f}^{2} ω_{f}, \end{matrix}

(4)

ahol

ω_{0}

a gáz szögsebessége a neutroncsillaghoz legközelebbi helyzetben.
Az (egységnyi gáztömegre felírt) energia megmaradásának tétele szerint

\begin{matrix} \frac{1}{2} (v_{0}^{2} + r_{0}^{2} ω_{0}^{2}) - \frac{G M}{r_{0}} = \frac{1}{2} v_{f}^{2} - \frac{G M}{r_{f}} . \end{matrix}

(5)

A (4), (5) egyenleteket, továbbá a közönséges csillag körmozgásának

\begin{matrix} r_{0} ω_{0}^{2} = \frac{G M}{r_{0}^{2}} \end{matrix}

(6)

feltételét kihasználva a keresett minimális távolságra

\begin{matrix} r_{f} = (\frac{v_{0} \sqrt[]{G M r_{0}} - G M}{v_{0}^{2} r_{0} - G M}) r_{0} \end{matrix}

adódik.

3. feladat. Magnetohidrodinamikai (MHD) generátor

a)

B

indukciójú mágneses mezőben

v

sebességgel mozgó

w

széles higanyszálban

U = v B w

feszültség indukálódik, melynek hatására

\begin{matrix} I = \frac{U}{R} = U \cdot {(\frac{ϱ w}{L h})}^{- 1} = \frac{v B L h}{ϱ} \end{matrix}

erősségű áram indul

- \hat{y}

irányban. Ekkora árammal átjárt vezetőre a mágneses tér

\begin{matrix} F = B I w = \frac{B^{2} L h w}{ϱ} v \end{matrix}

nagyságú,

- \hat{x}

irányú erőt fejt ki.

b)

A mágneses mező által kifejtett ,,fékező nyomás''

\begin{matrix} p_{fékező} = \frac{F}{h w} = \frac{v B^{2} L}{ϱ} . \end{matrix}

Ennek és a szivattyú eredeti

p

nyomásának ,,eredője'' állítja be a higany áramlási sebességét. Mivel a higany áramlási sebessége az eredő külső erővel (vagyis a szivattyú és a mágneses mező által együttesen kifejtett erővel) arányos (

v = α F

), felírhatjuk, hogy

\begin{matrix} v = α (p - p_{fékező}) = v_{0} - \frac{v v_{0} B^{2} L}{P ϱ}, \end{matrix}

ahonnan

\begin{matrix} v = v_{0} {(1 + \frac{v_{0} B^{2} L}{P ϱ})}^{- 1} = v_{0} \frac{P ϱ}{P ϱ_{+} v_{0} B^{2} L} . \end{matrix}

c)

A szivattyú többletteljesítményének fedeznie kell az időegységenként termelt Joule-hőt:

\begin{matrix} Δ P = U I = v_{0} B w \cdot \frac{v_{0} B L h}{ϱ} = \frac{v_{0}^{2} B^{2} w L h}{ϱ} . \end{matrix}

Ugyanerre az eredményre jutunk, ha a

v

sebességhez tartozó mágneses fékező nyomást (

v_{0} B^{2} L / ϱ

-t) megszorozzuk a

h w

keresztmetszettel és az áramlás

v_{0}

sebességével.

d)

n

törésmutatójú állóvízben a fény

v_{1} = c / n

sebességgel terjed. Ha a víz a laboratóriumban álló műanyagcsőhöz képest

v_{0}

sebességgel halad, akkor a fény sebessége a laboratóriumi koordináta-rendszerben

v_{0}

és

v_{1}

,,eredője'', amelyet azonban nem a klasszikus fizika aritmetikai összezésével, hanem a relativisztikus sebesség-összeadás

\begin{matrix} v_{eredő} = \frac{v_{0} + v_{1}}{1 + \frac{v_{0} v_{1}}{c^{2}}} = \frac{v_{0} + \frac{c}{n}}{1 + \frac{v_{0}}{c n}} \end{matrix}

képlete segítségével számítható ki. Ez a képlet a másodrendűen kicsiny (

v^{2} / c^{2}

-tel arányos) tagokat elhanyagolva egyszerűbb alakra hozható:

\begin{matrix} v_{eredő} = \frac{v_{0} + \frac{c}{n}}{1 + \frac{v_{0}}{c n}} \cdot \frac{1 - \frac{v_{0}}{c n}}{1 - \frac{v_{0}}{c n}} \approx \frac{c}{n} + v_{0} (1 - \frac{1}{n^{2}}) . \end{matrix}

A (laborbeli) terjedési sebesség

\begin{matrix} Δ v = v_{eredő} - v_{1} \approx v_{0} (1 - \frac{1}{n^{2}}) \end{matrix}

megváltozása az

L

hosszúságú út befutásához szükséges

T = L / v_{1}

időt

\begin{matrix} Δ T = L \cdot | Δ (\frac{1}{v_{1}}) | \approx \frac{Δ v}{v_{1}^{2}} L \approx \frac{L v_{0}}{c^{2}} (n^{2} - 1) \end{matrix}

értékkel lecsökkenti. Emiatt az

f

frekvenciájú fény belépő és kilépő fázisának különbsége is módosul, a fázistolás megváltozása

\begin{matrix} Δ ϕ = 2 π f Δ T \approx 2 π f \frac{L}{c^{2}} (n^{2} - 1) v_{0} . \end{matrix}

Megjegyzés. Az áramló vízben terjedő fény fázisának eltolódása (pontosabban az áramlással egyező és ellentétesen haladó fényhullámok fáziskülönbsége) interferenciakísérletben jól mérhető. Ilyen mérést elsőként H. Fizeau francia fizikus végzett 1851-ben. Mérési eredményei (melyek szerint az áramló vízben nagyobb ugyan a fény terjedési sebessége, mint álló közegben, de nem annyival, mint azt a klasszikus fizika alapján várnánk) a relativitáselmélet egyik fontos kísérleti bizonyítékát képezik.

Gnädig Péter‐Vankó Péter

¹A feladatok szövegét a KöMaL októberi számában közöltük.