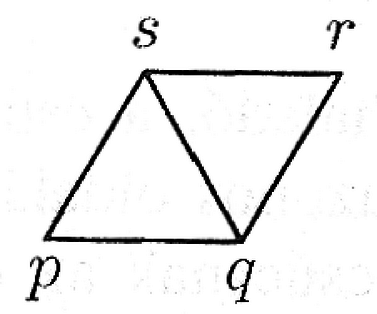Cím:	A 2000-2001. évi Arany Dániel Matematikai Tanulóverseny feladatai
Füzet:	2001/november, 461 - 466. oldal	PDF  |  MathML
Témakör(ök):	Arany Dániel

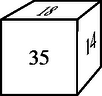
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   KEZDŐK Első forduló     Mindhárom kategória     1. Egy kocka minden lapjára egy-egy pozitív egész számot írtunk. Ezek közül az ábrán feltüntettünk három számot. Tudjuk, hogy a szemközti lapokon levő számok összege egyenlő, és a fel nem tüntetett számok mindegyike prímszám. (ld. I.1 ábra). Melyek ezek a számok?    (6 pont)   2. Az $A$ halmazt a páros természetes számok négyzeténél eggyel nagyobb számok, a $B$ halmazt a négyzetszámok háromszorosai alkotják. Határozza meg $A\cap B$-t! (Az $A$ és $B$ halmazok közös elemeiből álló halmazt jelöljük $A\cap B$-vel.) (6 pont)   3. Az $ABCD$ téglalap oldalai $AB=13$ cm és $BC=5$ cm. Az $AB$ oldalegyenesen milyen távolságra lehet az $A$ ponttól egy olyan pont, amelyből a $DA$ és $DC$ szakaszok egyenlő szögben látszanak? (Hány ilyen pont van?) (8 pont)   4. Igaz-e, hogy négy irracionális szám között mindig van három olyan, amelyek összege is irracionális szám? (10 pont)   5. 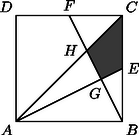Az $ABCD$ négyzet területe $60{\text{cm}}^2$. A $BC$ és $CD$ oldalak felezőpontjai $E$, illetve $F$. Az $AE$ és $BF$ szakaszok metszéspontja $G$, az $AC$ és $BF$ szakaszoké $H$. ( ld. I.5 ábra). Mekkora a $CHGE$ négyszög területe? (10 pont)   Második (döntő) forduló     I. kategória: Szakközépiskolások     1. Bizonyítsa be, hogy az $\begin{array}{c}{\displaystyle 1^{2001}+2^{2001}+\text{...}+{1999}^{2001}+{2000}^{2001}}\end{array}$ összeg osztható 2001-gyel!   2. Egy 10 cm befogójú egyenlő szárú derékszögű háromszögbe két olyan egyenlő sugarú kört írunk, amelyek érintik egymást és az átfogót, illetve egy-egy befogót. Mekkora a sugár pontos értéke?   3. Oldja meg a valós számok halmazán a következő egyenletet: $\begin{array}{c}{\displaystyle \left\{\frac{1}{2}x\right\}=\frac{1}{16}x+\frac{1}{32}\mathrm{,}}\end{array}$ ahol $\left\{z\right\}$ a $z$ valós szám törtrészét jelenti!       II. kategória: Általános matematika tantervű gimnáziumi tanulók     1. Azonos az 1. kategória 3. feladatával.   2. Melyek azok az $\left(x;y\right)$ egész számokból álló számpárok, amelyekre teljesül az alábbi egyenlőség: $\begin{array}{c}{\displaystyle 5x^2+2y^2-2xy+4x-4y=5?}\end{array}$   3. Az $ABC$ háromszög területe $t$, beírt körének sugara $r$. Az $A$ csúcsból induló két oldalt és a beírt kört kívülről érintő kör sugara $r_a$, a $B$ csúcsból induló két oldalt és a beírt kört kívülről érintő kör sugara $r_b$, a $C$ csúcsból induló két oldalt és a beírt kört kívülről érintő kör sugara $r_c$. A beírt kör és a másik három kör közös belső érintője egy-egy kis háromszöget vág le az $ABC$ háromszögből, amelyek területe rendre $t_a$, $t_b$, $t_c$. Igazolja, hogy $\begin{array}{c}{\displaystyle \frac{t_a}{r_a}+\frac{t_b}{r_b}+\frac{t_c}{r_c}=\frac{t}{r}!}\end{array}$       III. kategória: Speciális matematika tantervű gimnáziumi tanulók     1. Határozza meg az $x^4-15x^2-18x$ kifejezés legkisebb értékét, ha $x$ valós szám!   2. Azonos a 2. kategória 3. feladatával.   3. Mi lehet a pozitív egész értékű szigorúan monoton növekvő sorozat, ha $a_2=2$, továbbá relatív prím $m$ és $n$ esetén $a_{m\cdot n}=a_m\cdot a_n$?   HALADÓK Első forduló     I. kategória: Szakközépiskolai tanulók       1. Határozza meg az összes olyan pozitív egész számot, amelyre $\begin{array}{c}{\displaystyle 1!+2!+3!+\text{...}+n!}\end{array}$ egy egész szám négyzete! ($n!=1\cdot 2\cdot 3\cdot \text{...}\cdot n$, azaz 1-től $n$-ig az egész számok szorzata, ha $n>1$, egész és $1!=1$.)   2. Bizonyítsuk be, hogy ha tetszőleges négy egymást követő pozitív egész szám szorzatához $a)$  2000-et hozzáadunk, $b)$  2001-et hozzáadunk, akkor az eredmény sem prímszám, sem pedig négyzetszám nem lehet!   3. Legyen $e$ az $ABC$ háromszög $S$ súlypontján áthaladó, a csúcsok egyikét sem tartalmazó egyenes. Bizonyítsuk be, hogy az $e$ egyenes azonos oldalán lévő csúcsok $e$-től mért távolságainak összege megegyezik a harmadik csúcsnak az $e$ egyenestől mért távolságával!   4. Határozza meg a $k$ paraméter értékét úgy, hogy a $\begin{array}{c}{\displaystyle 4x^4-\left(4k+13\right)x^2+\left(9k+9\right)=0}\end{array}$ egyenlet valós gyökeit növekvő sorrendben felírva mindhárom szomszédos gyökpár különbsége ugyanannyi legyen!   5. Egy háromszög alapú gúla éleire olyan pozitív egész számokat írtunk, amelyekre igaz, hogy bármelyik csúcsba futó három élre írt számok összege ugyanakkora. Hányféle lehet a gúla éleire írt számok összege, ha az élekre írt számok szorzata 3600?       II. kategória: Általános tantervű gimnáziumi tanulók     1. Azonos az I. kategória 2. feladatával.   2. Azonos az I. kategória 3. feladatával.   3. Oldjuk meg a valós számok körében a következő egyenletet: $\begin{array}{c}{\displaystyle \frac{1+\sqrt[]{x+1}}{1-\sqrt[]{x+1}}+\frac{1-\sqrt[]{x+1}}{1+\sqrt[]{x+1}}-\frac{1}{\sqrt[]{x-1}}=\sqrt[]{x+1}\left(\frac{1+\sqrt[]{x+1}}{1-\sqrt[]{x+1}}-\frac{1-\sqrt[]{x+1}}{1+\sqrt[]{x+1}}\right)+\sqrt[]{x-1}\mathrm{.}}\end{array}$   4. Azonos az I. kategória 5. feladatával.   5. Melyek azok a nullától különböző $a$, $b$, $c$ számjegyek, amelyekre minden pozitív egész $n$ esetén teljesül, hogy az $n$-jegyű $\overline{aa\text{...}a}$ szám négyzetének és az $n$-jegyű $\overline{bb\text{...}b}$ számnak az összege egyenlő a $2n$-jegyű $\overline{cc\text{...}c}$ számmal?       III. kategória: Speciális matematika tantervű gimnáziumi tanulók     1. Bizonyítsuk be, hogy tetszőleges háromszögre $\begin{array}{c}{\displaystyle 18Rr\le ab+ac+bc\mathrm{,}}\end{array}$ ahol $R$ a köréírt, $r$ a beírt kör sugara, továbbá az oldalak hossza $a$, $b$ és $c$.   2. A $2000$ egység oldalú $ABC$ szabályos háromszöget az oldalakkal párhuzamos egyenesekkel egységoldalú szabályos háromszögekre daraboltuk. Az így keletkezett ${2000}^2$ db kis háromszög minden csúcsa mellé egy-egy valós számot írtunk. Az $A$, $B$, $C$ csúcsok mellé rendre az $a$, $b$, $c$ számot írtuk, a többire pedig úgy írtunk számokat, hogy minden olyan rombuszban, amely két, közös oldallal rendelkező kis háromszögből áll, a szemköztes csúcsok mellé írt számok összege egyenlő. Például: $p+r=q+s$ (ld. III.2 ábra) Határozzuk meg az eredeti $ABC$ háromszög kerületére írt számok összegét!   3. Egy háromszög oldalainak mérőszáma egész szám. A háromszögbe írható kör sugara egységnyi hosszúságú. Határozzuk meg az oldalak hosszát!   4. Adott $n$ pont a síkon úgy, hogy semelyik 3 sincs egy egyenesen. Bizonyítsuk be, hogy összeköthetők egy önmagát nem metsző zárt töröttvonallal!   Második forduló     I. kategória: Szakközépiskolai tanulók       1. Bizonyítsuk be, hogy a derékszögű háromszög területének mérőszáma megegyezik azon két szakasz hosszának szorzatával, amelyre a háromszögbe írható kör érintési pontja bontja az átfogót!   2. Oldjuk meg a valós számok halmazán a $\begin{array}{c}{\displaystyle 2\sqrt[]{|2x-5|}-\sqrt[4]{\left(2x-5\right)\left(x-2\right)}-\sqrt[]{|x-2|}\le 0}\end{array}$ egyenlőtlenséget!   3. Egy konvex négyszög egyik középvonala felezi a területét. Bizonyítsuk be, hogy a négyszög trapéz!   4. Bizonyítsa be, hogy nem létezik olyan konvex nyolcszög, amelynek szögei egyenlők, oldalai pedig valamilyen sorrendben 1, 2, 3, 4, 5, 6, 7 és 8 egység hosszúak!     II. kategória: Általános tantervű gimnáziumi tanulók     1. Tekintsük az $f\left(x\right)=x^2-\frac{a^2-1}{a}x-1$ ($a\ne 0$) függvényt, ahol $x\in \text{R}$. A függvény grafikonja az $y$ tengelyt egy, az $x$ tengelyt két pontban metszi. Bizonyítsuk be, hogy a három metszéspont által meghatározott háromszög területe nagyobb vagy egyenlő, mint 1.   2. Legyen $X$ egy adott $AB$ szakasz belső pontja. Vegyük fel a szakasz ugyanazon oldalára az $APX$ és $XQB$ szabályos háromszögeket! Legyen $M$ és $N$ az $AQ$, illetve $BP$ szakasz felezőpontja! Bizonyítsuk be, hogy $XMN$ háromszög szabályos, továbbá határozzuk meg azt az $X$ pontot, amelyre az $MN$ szakasz hossza minimális!   3. Jelölje $s\left(n\right)$ az $n$ szám 10-es számrendszerbeli alakjában a számjegyek szorzatát. Mennyi $\begin{array}{c}{\displaystyle s\left(2000\right)+s\left(2001\right)+s\left(2002\right)+\text{...}+s\left(3000\right)?}\end{array}$   4. Egy asztalon 2000 darab pénzérme van, mindegyik a ,,fej'' oldalával felfelé fordítva. Egy-egy alkalommal pontosan $k$ darab érmét a másik oldalára fordíthatunk. Bizonyítsuk be, hogy az adott művelet ismétlésével elérhető bármely adott $k$ szám esetén ($1\le k\le 2000$), hogy a 2000 érme ,,írás'' oldalával felfelé legyen fordítva!     Harmadik (döntő) forduló     I. kategória: Szakközépiskolások     1. Az $x$, $y$, $z$ egész számokra teljesül, hogy $\begin{array}{c}{\displaystyle \left(x-y\right)\left(y-z\right)\left(z-x\right)=x+y+z\mathrm{.}}\end{array}$ Bizonyítsuk be, hogy ekkor az $x+y+z$ összeg osztható 54-gyel!   2. Az $ABC$ hegyesszögű háromszög $AB$ oldalának tetszőleges belső pontja az $X$ pont. Az $AXC$ és $CXB$ háromszögek beírt körének az $AB$ egyenestől különböző közös külső érintője a $CX$ szakaszt az $Y$ pontban metszi. Bizonyítsuk be, hogy a $CY$ szakasz hossza független az $X$ pont megválasztásától!   3. Bizonyítsuk be, hogy bármely 1-nél nagyobb négyzetszám 2-es számrendszerben felírt alakja legalább 2 darab 0 számjegyet tartalmaz!       II. kategória: Általános tantervű gimnáziumi tanulók       1. Igazoljuk, hogy ha az $\left\{a_n\right\}$ sorozat első tagja egy 0-tól különböző egész szám, akkor $a_{n+1}=a_n^2+a_n-1$ esetén ($n\in {\text{Z}}^{+}$) az $\frac{a_n}{a_k}$ tört nem egyszerűsíthető, ahol $n$ és $k$ egymástól különböző pozitív egész szám!   2. Legyen az $ABC$ hegyesszögű háromszög $A$-ból induló magasságvonalának talppontja $T$. Az $AT$ szakasz mint átmérő fölé írt körnek az $AB$, illetve $AC$ oldallal való, $A$-tól különböző metszéspontja legyen $D$, illetve $E$. Bizonyítsuk be, hogy az $ABC$ háromszög köré írt körének középpontja az $ADE$ háromszög $A$-ból induló magasságvonalának egyenesén van!   3. Az $a$ és $b$ befogójú derékszögű háromszög beírt körének sugara $r$. Ha az átfogóhoz tartozó súlyvonal a beírt körből $r$ hosszúságú húrt metsz ki, akkor mekkora az $\frac{a}{b}+\frac{b}{a}$ értéke?     III. kategória: Speciális matematika tantervű gimnáziumi tanulók     1. Az $ABC$ hegyesszögű háromszög $AB$ oldalának tetszőleges belső pontja az $X$ pont. Az $AXC$ és $CXB$ háromszögek beírt körének az $AB$ egyenestől különböző közös külső érintője a $CX$ szakaszt az $Y$ pontban metszi. Mely $X$ pont esetén lesz az $AYB$ háromszög területe minimális?   2. Legyen a $H=\left\{n\mathrm{,}n+\mathrm{1,}n+\mathrm{2,}\text{...}\mathrm{,}n+4096\right\}$, ahol $n$ páratlan természetes szám. Bizonyítandó, hogy $H$ elemei két diszjunkt $A$ és $B$ halmazba oszthatók úgy, hogy egyszerre teljesül a következő két feltétel: $a)$  $A$ elemszáma 2000, $b)$  $A$ és $B$ elemei felírhatók egy-egy kör kerületére úgy, hogy a szomszédos számok relatív prímek.   3. 2001 darab különböző pozitív egész számról tudjuk, hogy a számok szorzatának pontosan 2000 darab különböző pozitív prímosztója van. Bizonyítsuk be, hogy a 2001 darab szám közül kiválasztható egy vagy több úgy, hogy azok szorzata négyzetszám legyen (vagy az egy kiválasztott szám már maga is négyzetszám)!