Kezdőlap


Cím:	Cardano és a kriptográfia - A rejtjelező-rácsok matematikája
Szerző(k):	Dénes Tamás
Füzet:	2001/szeptember, 325 - 335. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

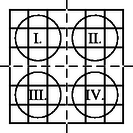
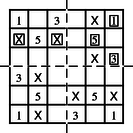
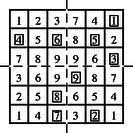
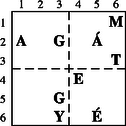
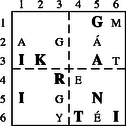
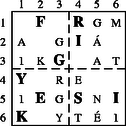
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Girolamo Cardano születésének 500. évfordulójára ajánlva

Bevezetés

0. ábra

Éppen csak elkezdődött a XVI. század, amikor Girolamo Cardano (1501‐1576) olasz matematikus, fizikus, filozófus, orvos, (egyszóval igazi reneszánsz tudós) (0. ábra) megszületett. 1545-ben megjelent munkája, az Ars Magna képleteket tartalmaz az általános alakú harmadfokú egyenlet gyökeire. Az utókor számára Cardano nevével általában ezen eredményei kapcsolódnak össze, pedig a mai napig kétséges, hogy ezeket a képleteket valóban ő fedezte-e fel.¹
Ugyanakkor kevesen ismerik Cardanot mint a XVI. századi kriptográfia egyik legjelentősebb alakját. Ez nem annyira meglepő, hiszen természeténél fogva a kriptográfiát (a titkosírást, vagy rejtjelezést) ,,zárt ajtók mögött" művelték. Királyok, hadvezérek szigorúan bizalmas levelezését bonyolították különböző módszerekkel titkosított levelekkel. Mivel a bonyolultabb rejtjelezési módszerek és főleg azok megfejtése legtöbbször komoly matematikai ismereteket igényel, így érthető, hogy többnyire neves matematikusok nevéhez fűződik a kriptográfia elméleti alapjainak megteremtése.
Cardano egy akkor egészen új rejtjelezést dolgozott ki, amelyet ma Cardano-rácsnak neveznek. A Cardano-rács sikerét mi sem bizonyítja jobban, mint hogy 400 évvel később, a XX. század közepén, a nyugatnémet hírszerző szerv (BND = Szövetségi Információs Szolgálat) még használta.
A következőkben rövid történeti áttekintés után bemutatjuk a Cardano-rács alapgondolatát, majd annak több irányú általánosítását és néhány matematikai tulajdonságát.

Fáklyatávíró és intervallum rejtjelezés

Cardano behatóan tanulmányozta az előző korok rejtjelezési technikáit egészen az ókorig visszatekintve. Így akadt rá az i.e. II. században élt Polübiosz nevű görög történész leírására, amelyben egy érdekes és az addig megszokottól merőben különböző eljárást ír le.

Polübiosz fáklyatávírója

Készítsük el az 1. ábrán látható 5 sorból és 5 oszlopból álló táblázatot.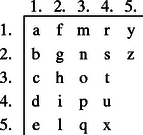

1. ábra

Az üzenetet küldőnél 10 fáklya van, 5-5 mindkét kezénél. Az üzenetet betűnként küldi el úgy, hogy a bal kezével annyi fáklyát emel föl, ahányadik sorban, a jobb kezével pedig annyit, ahányadik oszlopban helyezkedik el a küldendő betű a táblázatban. Például a ,,t" betű esetén a bal kezében 3, míg a jobb kezében 4 fáklya van.
,,Ezt a módszert Cleoxenusz és Demokritosz találta ki, de én tökéletesítettem.'' ‐ írja büszkén Polübiosz.
Joggal lehetett büszke, mert bár a fáklyával történő üzenet továbbítást már a régi kínaiak ² is ismerték, az ő rendszere volt az első táblázatba foglalt rejtjelező eljárás, amelynek nagy előnye, hogy ─ a módszer megváltoztatása nélkül ─ könnyen cserélhető a táblázatbeli ABC, illetve a táblázatbeli betűk elhelyezése.

Kérdés: A fenti

22

betűs ABC betűi hányféleképpen helyezhetők el a táblázatban? És ha kitöltjük mind a

25

betűhelyet a táblázatban?

Ezt az eljárást fejlesztette tovább Cardano úgy, hogy az ABC betűinek megadásához csak két fáklyát használt (egyet-egyet mindkét kézben) és a fáklyák elhelyezkedése, illetve egymáshoz való viszonya kódolta a megfelelő sort és oszlopot.
Ez a módszer adhatta Cardanonak az ötletet, hogy megalkossa a táblázaton alapuló titkosírás két nagy családját. Az egyik az ,,intervallum rejtjelezés", amelyben az üzenet titkosítása a betűk közötti távolságokon alapul. A módszert az egyszerűség kedvéért egy példán mutatjuk be. Készítsük el a 2. ábrán látható táblázatot.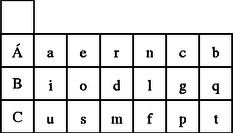

2. ábra

Legyen az üzenet: csacsi. (A lépéseket a 3. ábrákon követhetjük.) Írjuk az üres levélpapír bal felső sarkába az Á, B, C betűk bármelyikét. Ez csupán a szöveg kezdetét jelöli (C). Helyezzük a táblázat üres négyzetét a megjelölt betűre, majd a csacsi első betűjét (c) tartalmazó, nagybetűvel jelzett mező jelét (Á) írjuk a papírra pontosan a c betű fölé (lásd 3.a) ábra). Most helyezzük a táblázat üres négyzetét az utoljára felírt nagybetűre, és keressük ki a táblázatból a következő betűt, az ,,s"-et. Ezzel ugyanúgy járunk el, mint az előzőkben, azaz a táblázatbeli s betű fölé írjuk a papírra a mező jelét (C). A fenti lépéseket addig folytatjuk, amíg van hely a levélpapír adott sorában, majd a legelső lépést megismételve új sort nyitunk, és az eljárást folytatjuk a küldendő szöveg végéig. A megfejtő dolgát azzal nehezítjük meg, hogy az üresen maradt helyeket tetszőleges, Á, B, C-től különböző betűkkel töltjük ki (lásd 3.b) ábra). (Még jobb, ha értelmes szöveggé tudjuk kiegészíteni a rejtett szöveget, de ez nem feltétlenül szükséges.)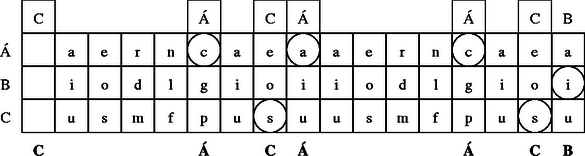

3.a) ábra

\begin{matrix} \begin{matrix} C & S & O & R & O & G & A & T & E & A & A & F & A & L & O & N & Á & L & M & O & S & C & S & I & G & A & B & Á & R & E & L & É & G & L & A & S & S & A & N & K & I & M & Á & S & Z & H & A & T & N & A & C & S & E & N & D & B & E & N \\ ↓ & ↓ & ↓ & ↓ & ↓ & ↓ & ↓ \\ kezdőpont & (c) & (s) & (a) & (c) & (s) & (i) \end{matrix} \end{matrix}

3.b) ábra

Az üzenet fogadójánál természetesen ugyanolyan táblázat van, mint a küldőnél. Így a fenti eljárást a kezdőponttól elvégezve olvashatóvá válik az üzenet. Mai szemmel ez az eljárás érdekes, de nem túl praktikus, mivel a táblázat használata elég nehézkes, és sok helyet használ az információtartalomhoz képest. Cardano a nehéz érthetőség kritikáját több kortársától is megkapta, akik akkor még nem tudhatták, hogy módszerével Cardano messze megelőzte korát, és elvetette a nem szimmetrikus rejtjelezés alapjait. A fenti eljárás ugyanis az addig szokásostól eltérően nem csupán betű-betű megfeleltetés, azaz betűhelyettesítés³, hanem többértelmű megfeleltetés: a három nagybetű nindegyike 6-6 kisbetűt kódol, így a megfejtéshez többlet információra van szükség (a betű elhelyezkedése a sorban, vagyis távolsága a viszonyítási betűtől). Ellentétben tehát az egyszerű betűhelyettesítéssel, itt az üzenet és a rejtjelezett szöveg betűstatisztikája egyáltalán nem egyezik meg!

A Cardano-rács

A táblázaton alapuló másik módszercsalád, ami a mai napig is Cardano nevét viseli, az úgynevezett Cardano-rács. A rács itt egy betűkből álló mátrixot jelent. Hogy miről is van szó, ahhoz idézzük fel magának Cardanonak a szavait⁴:
,,Végy két azonos méretű pergamen lapot, és azonos vonalak mentén készíts kivágásokat⁵ különböző helyeken. Ezek a kivágások legyenek kicsik, de mégis legalább akkorák, mint az ABC nagybetűi. Az összes kivágásokba összesen 120 betűt lehessen elhelyezni. Az egyik pergamen lapot majd a levelező társadnak adod. Amikor alkalom adódik, először írd az üzenetedet olyan tömören, ahogy csak lehetséges, így az üzenet kevesebb betűt is tartalmazhat, mint amennyi a kivágott ablakokban elhelyezhető. Amikor beírtad az üzeneted az egyik pergamen lapra, tedd ugyanezt a másikkal is. Ezután töltsd ki az első lapon az üresen maradt helyet úgy, hogy teljes mondatokra egészítsék ki a már ráírt szöveget. Ez a kitöltés úgy történjen, hogy a teljes szöveg stílusa és tartalma összefüggő és egységes legyen. Amikor a levelező társad megkapja a te üzenetedet, ráhelyezi a megfelelő kivágásokkal ellátott pergament, és így elolvashatja az üzenetet."
A rejtjelező rács figyelemre méltó ,,divattá" vált a kriptográfiában. A Cardano-rács sikerét talán annak köszönheti, hogy egyszerű, de mégis fantasztikus változatosságot biztosít. Ekkora siker nagyon ritkán tapasztalható a tudomány, hát még a kriptográfia történetében. Hiszen az ismeretek állandó bővülésével a titkok megfejtésének technikája általában utoléri a titkosítók technikáját. Bár Cardano neve e téren nem vonult be a köztudatba, rejtjelező rácsa 450 éven át fennmaradt, sőt még a szépirodalomba is bevonult. Jules Verne: Sándor Mátyás című regényében éppen ilyen rejtjelező rács birtokába jutva fejti meg Sándor Mátyás elfogott titkos üzenetét a két gonosz, Torontál és Sárkány. A titkos levél és a megfejtéséhez szükséges rács már a regény elején megjelenik, és így a további cselekmény egyik ,,főszereplőjévé" válik.
Alábbi példánkban egy

6 \times 6

-os rácsot mutatunk be, amelyben felfedezhető bizonyos rokonság az úgynevezett intarzia játékkal is⁶. A 4. ábra rácsába Karinthy Frigyes saját intarziáját írtuk be. Így még érdekesebb, hogy ugyanabban a szövegben mennyi különböző szöveg lehet elrejtve. Az 5., 6., 7. ábrákban megvastagított számok a Cardano-rács kis ablakait jelölik, azaz a 4. ábrára pontosan ráhelyezve és az ablakok helyén levő betűket balról jobbra haladva soronként lefelé összeolvasva megkapjuk a rejtett szöveget.
A 4. ábrába beírt szöveg: ,,MAGÁT EGY ÉGI KAR INTI FRIGYE SIKERÜLNI FOG"
Az 5. ábra rácsával kiolvasható rejtett szöveg: ,,MÁTÉ KINT INOG".
A 6. ábra rácsával kiolvasható rejtett szöveg: ,,EGYÉK INGYEN".
A 7. ábra rácsával kiolvasható rejtett szöveg: ,,AGG KINT FIGYEL".
Egy

n \times n

-es rácsba (amelyben

n

sor és

n

oszlop van)

n^{2}

betűből álló szöveget írhatunk be. Ha az elrejtendő szöveg

k

betűből áll (ahol természetesen

k < n^{2}

) akkor a

k

ablakot tartalmazó rácsok száma

(\binom{n^{2}}{k}) = \frac{n^{2}!}{k! (n^{2} - k)!}

. Hogy ez mekkora változatosságot jelent, annak illusztrálására nézzük az 5. ábra rácsát, itt

n = 6

k = 12

, a lehetséges különböző rácsok száma tehát

\begin{matrix} \frac{36!}{12! \cdot 24!} = 31 \cdot 29 \cdot 28 \cdot 25 \cdot 17 \cdot 13 \cdot 9 = 1 251 677 700. \end{matrix}

4, ábra

5. ábra

6. ábra

7. ábra

Ugyanígy számítható ki a 6. ábrára (

n = 6

k = 11

) és a 7. ábrára (

n = 6

k = 13

) a lehetséges rácsok száma.

Fordítsunk a rácson!

A Cardano-rács előzőkben leírt egyszerű képzési eljárása (ablakok tetszőleges kivágása) után ─ a továbbiakban ezt egyszerű rácsnak nevezzük ─ mutatunk egy másik rács-előállítási és -kitöltési módszert, amelyet forgató-rácsnak neveznek.
A forgató-rács olyan rejtjelező eszköz, amely 90 fokonként elforgatva ablakaival pontosan egyszer lefedi a hozzá tartozó betűmátrix összes mezőjét.
Itt tehát már nem lehet tetszőlegesen kivágni a rács ablakait, hiszen az elforgatások során ugyanarra a mezőre nem kerülhet több ablak. A rács ablakait úgy kell kijelölni, hogy elforgatáskor valamennyi ablak mindig más és más helyre kerüljön. Látható, hogy a forgató-rács előállításához szükséges, hogy a rács mérete,

n

páros legyen. Ha ugyanis a kivágható ablakok száma

k

, akkor ahhoz, hogy az

n^{2}

mező mindegyikére a rács négy helyzete során pontosan egyszer kerüljön ablak,

k = \frac{n^{2}}{4}

ablakra van szükség.
A forgató-rács előállítását is egy konkrét példán keresztül mutatjuk be.
Legyen a rács mérete

n = 6

, ekkor tehát

k = 9

ablakot kell kivágnunk.
1. lépés: Osszuk fel a

6 \times 6

mezőt tartalmazó mátrixot négy zónára a 8. ábra szerint. Így az I‐IV. zónák mindegyikébe pontosan kilenc mező esik.

8. ábra

9. ábra

10. ábra

11. ábra

2. lépés: Válasszunk ki az I. zóna kilenc mezőjéből

k_{1}

számút, ahol

1 \leq k_{1} \leq 9

. Példánkban

k_{1} = 2

, és a 4. és 6. mezőt választottuk (lásd 9. ábra).

3. lépés: Forgassuk el a rácsot először 90 fokkal, és jelöljük meg a II. zónában azokat a mezőket, melyeket a kiválasztott (4. és 6.) mezők fednek. Majd forgassuk tovább a rácsot 90 fokonként, és jelöljük be ugyanígy a többi zónában is a fedett mezőket (lásd 9. ábra). Így a

k_{1}

ablak kijelölésével, négy forgatás után

4 \cdot k_{1}

mező válik foglalttá.

4. lépés Most a II. zónában válasszunk a még nem foglaltakból

k_{2} = 3

mezőt. Példánkban ezek az 1., 3., 5. mezők (lásd 10. ábra, ahol X jelöli a már foglalt mezőket, a bekeretezett számok jelölik az ablak-kivágásokat, a zóna számozása pedig értelemszerűen az I. zóna számozásának

90^{\circ}

-os elforgatottja). A négy elforgatással így újabb

4 k_{2}

mező válik foglalttá.
5. lépés: A fentiekhez hasonlóan végezzük el ugyanezt a III. és IV. zónákban is. Ekkor

4 k_{1} + 4 k_{2} + 4 k_{3} + 4 k_{4} = n^{2}

, azaz az ablakok számára valóban

k = k_{1} + k_{2} + k_{3} + k_{4} = 9

adódik⁷ (lásd 11. ábra, ahol a bekeretezett számok jelölik a kivágott ablakokat).
Vegyük észre, hogy a

k

ablak mindegyikét szabadon jelölhetjük ki az I‐IV. zónák valamelyikében, így az összes lehetséges (maximális számú ablakot tartalmazó)

n \times n

-es forgatórácsok száma

4^{k} = 4^{\frac{n^{2}}{4}}

. Példánkban ez

4^{9} = 262 144

Kérdés: Azonos

n

rácsméret és

k

ablakszám esetén forgató-, vagy egyszerű rácsból van-e több?

Megelőlegezzük a választ, amelyre az Olvasó jut e kérdés megválaszolása során: azonos rácsméret és ablakszám esetén nagyságrendekkel több a lehetséges egyszerű rácsok száma. Ugyanakkor rejtjelezési szempontból ez az összehasonlítás sántít, mivel az egyszerű rács betűmezőinek csak egy részében van a rejtett szöveg, míg a forgató-rácsnak mind az

n^{2}

mezőjét felhasználhatjuk a rejtett szöveg beírására⁸.
Illusztrációként bemutatjuk a 3. ábra szövegének a 11. ábra forgató-rácsával való rejtjelezését (lásd 12., 13., 14., 15. ábra).

12. ábra

13. ábra

14. ábra

15. ábra

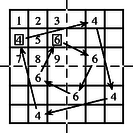
1. lépés: Rajzoljunk egy üres lapra akkora négyzetet, mint a forgató-rácsunk mérete, és helyezzük rá a rácsot.
2. lépés: Balról jobbra és fentről lefelé haladva írjuk a rács ablakaiba a szöveg kilenc betűjét.
3. lépés: Forgassuk el a rácsot 90 fokkal, és ismételjük meg a 2. lépést.
4‐5. lépés: Ismételjük meg a 3. lépést még kétszer.
A 15. ábra betűmátrixát kapjuk eredményül, amelyet elküldünk a címzettnek, aki a rács birtokában az 1‐5. lépésekhez hasonló módszerrel el tudja olvasni az üzenetet. Példánkban külön érdekesség, hogy az így megfejtett szövegből az 5., 6., 7. ábra egyszerű rácsaival újabb rejtett szövegek olvashatók ki.
A Cardano-rács történetének másik érdekessége, hogy pontosan Cardano Ars Magna-jának megjelenése után 250 évvel, 1795-ben jelent meg Carl Friedrich Hindenburg német matematikus könyve (lásd [4]), amelynek VI. fejezetét teljesen a rejtjelezésnek, ezen belül a rejtjelező rácsoknak szenteli. Nem a Cardano-rácsnak, mert (a tudománytörténetben nem szokatlan módon) Cardano nevét meg sem említi.
Hindenburg könyve nem csupán pontos leírását adja a Cardano-rácsnak, hanem bizonyos továbbfejlesztését is bemutatja. Ennek lényege, hogy ha a rács oldalait megjelöljük az

a

b

c

d

betűkkel, akkor a rácsforgatásokat megadhatjuk, mint e négy betű egy-egy permutációját. Ezzel a különböző rácsok számát

4! = 24

-szeresére növelhetjük.

Kérdés: Hogyan módosul a rácsforgató algoritmus a permutációs forgatás esetén?

Amint azt a következőkben látni fogjuk, a permutációknak nemcsak a rácsok kitöltésében van nagy szerepe, hanem a rácsok ablakainak meghatározásában is.

Permutációk, latin négyzetek és rejtjelező rácsok

Latin négyzetnek olyan

n \times n

-es négyzetes mátrixot nevezünk, amelynek minden sora és minden oszlopa az 1, 2,

...

n

számoknak egy permutációja.
Egy

n \times n

-es mátrixot permutációs mátrixnak nevezünk, ha a mátrix pontosan

n

darab 1-est tartalmaz úgy, hogy minden sorban és oszlopban pontosan egy 1-es áll, a többi elem pedig nulla.
Egyszerű, de a rejtjelező rácsok szempontjából fontos eredmény (lásd [1]) a következő:
Minden

n \times n

-es

L (n)

latin négyzet egyértelműen felírható

n

darab permutációs mátrix segítségével a következő alakban:

\begin{matrix} L (n) = 1 \cdot P_{1} + 2 \cdot P_{2} + ... + n \cdot P_{n}, \end{matrix}

(1)

éspedig úgy, hogy a

P_{k}

permutációs mátrixban éppen ott szerepel

1

, ahol

L (n)

-ben

k

van, a többi eleme pedig nulla.

(Az ,,összeadás" művelet a mátrixok ugyanazon helyén álló elemeinek összeadását, míg a ,,számmal való szorzás" a mátrixok minden elemének a megszorzását jelenti.)
Az így adódó permutációs mátrixok rejtjelező rácsként használhatók fel. Az eljárást a következő példán keresztül mutatjuk be:

\begin{matrix} \begin{matrix} L (4) = [\begin{matrix} 1 & 2 & 3 & 4 \\ 3 & 4 & 2 & 1 \\ 2 & 1 & 4 & 3 \\ 4 & 3 & 1 & 2 \end{matrix}] \\ P_{1} = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{matrix}], P_{2} = [\begin{matrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}], P_{3} = [\begin{matrix} 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \end{matrix}], P_{4} = [\begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \end{matrix}] . \end{matrix} \end{matrix}

Mindegyik

P_{i}

permutációs mátrix egy olyan rejtjelező rácsként fogható fel, ahol az 1-esek helyén vannak az ablakok. Így a forgatás helyett most a permutációs mátrixokat kell ‐ mint rácsokat ‐ egymás után a betűmátrixra helyezni ahhoz, hogy a titkosított szöveget beírjuk, illetve kiolvassuk. Mivel a fenti egyértelmű felbontási tétel miatt az így készített rácsok ablakai pontosan lefedik a betűmátrix

n^{2}

mezőjét, ezzel a módszerrel a teljes betűmátrixot kitölthetjük rejtjelezett szöveggel, akárcsak a forgató-rácsoknál. További előny, hogy a latin négyzet felbontásának egyértelműsége nem sérül, ha a felbontást adó permutációs mátrixok (rácsok) sorrendjét megváltoztatjuk. Így a lehetséges rácsfelhasználások száma a felbontások számának

n!

-szorosa.⁹
A rácsok tényleges alkalmazását megnehezíti terjedelmes helyigényük, hiszen

n

karakter betűmátrixba írásához szükség van a teljes permutációs mátrixra, és ehhez, bináris mátrix lévén,

n^{2}

byte tárolását kell biztosítani. Ha a permutációs mátrixokat megszámozzuk, azaz bármely

n \times n

-es permutációs mátrixhoz kölcsönösen egyértelműen hozzárendeljük az 1, 2,

...

n

számok egy permutációját, akkor a tárigény csökken.

Egy ilyen számozáshoz csak a mátrixban szereplő 1-esek megfeleltetésére van szükség, mivel az összes többi helyen nulla van. Legyen a permutációs mátrix

i

-edik sorának

j

-edik oszlopában 1-es. Ekkor a megfelelő permutáció

i

-edik eleme legyen a

j

. A permutációs mátrix definíciója szerint mindegyik sorban csak egy 1-es lehet, így valóban permutációt kapunk.
Ezek után a permutációkat egy megfelelő algoritmus (lásd [2]) segítségével sorszámokkal láthatjuk el 1-től

n!

-ig; ha a permutációs mátrixokat rejtjelező rácsként használjuk, akkor a mátrix, illetve az ehhez tartozó permutáció helyett elegendő a megfelelő sorszámot elküldeni a rejtjelezett üzenettel.
Az 1, 2,

...

n

számok egy permutációjának a tárolásához

c (n)

darab karakterre van szükség, ahol

\begin{matrix} c (n) = ([lg n] + 1) n \end{matrix}

(2)

n!

szám számjegyeinek száma (jelöljük

j (n)

-nel):

\begin{matrix} j (n) = [lg n! + 1] . \end{matrix}

(3)

Ekkor

\begin{matrix} \frac{j (n)}{c (n)} = \frac{[lg n! + 1]}{n ([lg n] + 1)} = \frac{\sum_{i = 1}^{n} lg i + 1}{n ([lg n] + 1)}, \end{matrix}

(4)

és ezért

\begin{matrix} {lim}_{}^{}_{n \to \infty}^{} \frac{j (n)}{c (n)} = 1. \end{matrix}

(5)

Ez a megfeleltetés mégis jól használható a gyakorlatban, mivel a használatos értékekre az 1. táblázat értékei adódnak. Ez azt mutatja, hogy 25‐50% megtakarítást érhetünk el, ha a permutáció helyett annak sorszámát tároljuk, illetve küldjük el.

\begin{matrix} n & j (n) & c (n) & \frac{j (n)}{c (n)} \\ 10 & 7 & 20 & .35 \\ 100 & 158 & 300 & .526 \\ 200 & 375 & 600 & .625 \\ 300 & 615 & 900 & .683 \\ 400 & 869 & 1200 & .724 \\ 500 & 1134 & 1500 & .756 \end{matrix}

1. táblázat

A Cardano-rács általánosítása:

k

-rács (pókháló-rács)

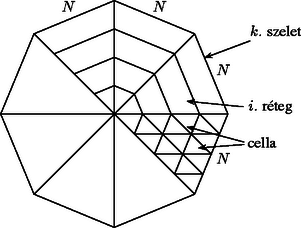
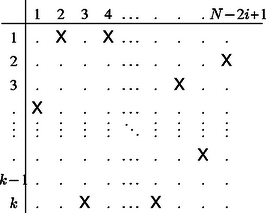
Cardano és Hindenburg is négyzet alakú rácsokkal dolgozott. Megmutatjuk, hogy tetszőleges szabályos

k

-szögre értelmezhető a rejtjelező rácsmodell.
Tekintsük a 16. ábra szerinti konstrukciót. Ez egy

k

oldalú szabályos sokszög, amelynek mindegyik oldala

N

egység hosszú, azaz mindegyik szeletének legkülső rétege

N

darab cellát tartalmaz. Minden szeletben

\frac{N}{2}

réteg és az

i

-edik rétegében

N - (2 i - 1)

cella van. Ebből következik, hogy az egy szeletben levő összes cellák száma:

\begin{matrix} \sum_{i = 1}^{\frac{N}{2}} N - (2 i - 1) = \frac{N^{2}}{4} . \end{matrix}

A teljes

k

-rács celláinak száma tehát

k \frac{N^{2}}{4}

. (A Cardano-rács esetében

k = 4

, amelyre valóban a négyzetrács celláinak számát kapjuk.)
Természetesen a

k

-rács forgatási szöge most nem

90^{\circ}

, hanem

\frac{360^{\circ}}{k}

. Az igazi problémát a rács ablakainak elhelyezése jelenti. Tekintsük az alábbi mátrixot (lásd 17. ábra), amelynek

k

sora, (ez felel meg a

k

-rács szeleteinek) és

N - 2 i + 1

oszlopa van (az

i

-edik réteg cellaszámának megfelelően).

16. ábra

17. ábra

A 17. ábrán az X ablak kivágást jelöl. A forgató-rács szabályait figyelembe véve a mátrix minden oszlopában pontosan egy ablak lehet. Ebből adódik, hogy az

i

-edik rétegben

k^{N - 2 i + 1}

ablak-kombináció lehetséges.
Mivel a rétegek elrendezései függetlenek egymástól, így a

k

-rács összes ablak-kombinációinak száma, azaz a különböző

k

-rácsok száma:

\begin{matrix} F R_{k}^{N} = \prod_{i = 1}^{\frac{N}{2}} k^{N - 2 i + 1} = k^{\sum_{i = 1}^{\frac{N}{2}} N - 2 i + 1} = k^{\frac{N^{2}}{4}} . \end{matrix}

(6)

Láthatjuk, hogy

k = 4

esetén ez pontosan a különböző Cardano-rácsok számát adja. A Hindenburg-féle permutációs forgatás itt is alkalmazható, csak itt egy

k

jelből álló sorozatot használunk, és így

k!

-szorosára nő a rácsvariációk száma. Az alábbi 2. táblázatban érdekességként bemutatjuk néhány rácsmérethez tartozó

k

-rácsoknak a számát.

\begin{matrix} k & N & F R_{k}^{N} & k & N & F R_{k}^{N} \\ 3 & 4 & 81 & 4 & 10 & 1 125 899 906 842 624 \\ 3 & 6 & 19 683 & 5 & 4 & 625 \\ 3 & 8 & 43 046 720 & 5 & 6 & 1 953 125 \\ 3 & 10 & 847 288 598 528 & 5 & 8 & 152 587 894 784 \\ 4 & 4 & 256 & 6 & 4 & 1 296 \\ 4 & 6 & 262 144 & 6 & 6 & 10 077 696 \\ 4 & 8 & 4 294 967 296 & 6 & 8 & 2 821 109 841 920 \end{matrix}

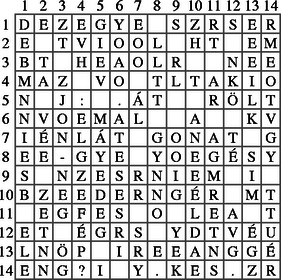
2. táblázat

Végül a 18. ábrán megadunk egy rejtjelezett négyzetes szövegmátrixot, amelyhez tartozó Cardano-rácsot a 19. ábrán (az ábrán a négyzetek jelölik az ablakokat) találjuk. A szöveg megfejtése (talán tartalma is) tanulságos lehet, a rácsot pedig újabb szövegek rejtjelezésére is felhasználhatja a kedves Olvasó.

18. ábra

19. ábra

Irodalomjegyzék

[1] J. Dénes‐A. D. Keedwell: Latin squares and 1-factorizations of complete graphs I. Ars Combin. 25A, 1988. 109‐126.
[2] Dénes Tamás: Algoritmusok az összes

n

-edfokú permutáció előállítására, Információ Elektronika, 1975. 1‐2.
[3] Philip J. Davis, Reuben Hersh: A matematika élménye, Műszaki Könyvkiadó, Budapest 1984.
[4] Carl Friedrich Hindenburg: Urchid der Reinen und Angewandten Mathematic herausgegeben von Carl Friedrich Hindenburg, Leipzig, 1795.
[5] Lukácsy András: Elmés játékok, játékos elmék, Minerva Kiadó, Budapest, 1960.
[6] Charles J. Mendelsohn: Cardan on cryptography, Scripta Math., 1938.
[7] Révay Zoltán: Titkosírások, Zrínyi Katonai Kiadó, Budapest, 1978.
[8] Sain Márton: Matematikatörténeti ABC, Tankönyvkiadó, Budapest, 1974.
[9] Sain Márton: Nincs királyi út! (matematikatörténet), Gondolat Kiadó, 1986.
[10] Simonyi Károly: A fizika kultúrtörténete, Gondolat Könyvkiadó, Budapest, 1986.
[11] B. L. van der Waerden: Egy tudomány ébredése, Gondolat Könyvkiadó, Budapest, 1977.

Dénes Tamás

¹ A matematika-történészek szerint egy bizonyos Scipione del Ferro (1465‐1526) megtalálta az általános alakú harmadfokú egyenlet megoldását, melyet közölt kollégáival. Ez 1515 körül történhetett, amikor Olaszországban gyakran tartottak matematikai versenyeket. Ferro egyik kollégája azt javasolta Niccolo Tartaglia (1500‐1557) akkori nagyképzettségű matematikusnak, hogy oldjanak meg harmadfokú egyenleteket. Tartaglia a kijelölt határidő előtt megoldotta az egyenleteket, módszerét azonban titokban tartotta. Cardano kitartó érdeklődésére elmondta neki a megoldást, de megeskette, hogy hallgat róla. Cardano azonban nem tartotta meg esküjét és 1545-ben az Ars Magna-ban ismertette a harmadfokú egyenlet megoldásának módszerét. Így kezdődött a heves, ádáz vita Tartaglia és Cardano között, amelynek végére a matematika-történet a mai napig nem tudott pontot tenni.

²A Kínai Nagy Falon már 2000 évvel ezelőtt, száz méterenként felállított fáklyások útján tudtak több száz kilométerre, nagyon gyorsan (és pontosan) üzeneteket eljuttatni.

³A betű-betű megfeleltetés azt jelenti, hogy az üzenet minden betűjéhez valamely szabály szerint egy ABC más betűjét rendeljük hozzá. A kriptográfiában ezt nevezik helyettesítésnek. Az így rejtjelezett szöveg betűinek eloszlása tehát pontosan megegyezik az eredeti szöveg betűinek eloszlásával.

⁴ Az idézet Charles J. Mendelsohn: Cardan on cryptography [6] cikkéből származik.

⁵kis ablakokat

⁶Az intarzia játék a szórejtésnek egy sajátságos neme, amelyben az a cél, hogy bizonyos szavakat (többnyire személyneveket) kell folyamatosan elhelyezni egy másik szövegben. Karinthy, Kosztolányi, Molnár Ferenc és mások kedvelt kávéházi szórakozása volt az intarzia játék. Az egyik legsikeresebb intarzia Kosztolányié: Vendég panasza az étkezdében: ,,Itt rossz a koszt, ó lány, ide zsörtölődni jár csak az ember." Az intarzia a rejtjelezéshez képest valóban csak játék, hiszen elegendő a rejtett szöveg első betűjét megtalálni, abból már a teljes intarzia-szöveg kiolvasható, míg a Cardano-rácsnál minden ablak helyét külön-külön meg kell fejteni ahhoz, hogy a rejtett szöveg kiolvasható legyen.

⁷ Természetesen az ablakok száma lehet ennél kevesebb is, de akkor a rács a négy körbeforgatás során nem fedi le az összes betűmezőt, így nem írhatjuk tele a szövegmátrixot.

⁸Az egyszerű ráccsal történő rejtjelezésnél a rejtett szöveg betűinek sorrendje nem változik, míg a forgató-rács összekeveri a rejtendő szöveg betűit. A kriptográfiában a betűk helyettesítése és a betűk keverése a két alapvető módszercsalád, amelyeket önmagukban, vagy együttesen használ fel. A forgató-rács nagy előnye kriptográfiai szempontból, hogy lehetővé teszi a két módszer egyesítését. Érdemes tehát felfigyelni arra, hogy a rejtjelezési eljárásoknál nem elegendő csupán mennyiségi megfontolásokat figyelembe venni!

⁹ Helyhiány miatt csak utalni tudunk a latin négyzetek azon léyeges tulajdonságára, hogy minden latin négyzet egy művelettáblaként fogható fel, amely műveletek bizonyos feltételek mellett, a rejtjelezés szempontjából igen kedvező tulajdonságokkal rendelkeznek (nem kommutatív, nem asszociatív). Egy következő cikkben térünk ki eme előnyös tulajdonságok és a napjainkban általánosan elterjedt, ,,számelmélet alapú" módszerek összevetésére.