|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Niccolo Fontana 1499-ben született az itáliai Brescia városában. Egy szegény lovasküldönc fia, édesapját hatéves korában elveszti, s így árvaságra jut. 1512-ben a Brescia városában fosztogató és gyilkoló francia zsoldosok elől a nők és a gyerekek egy templomba menekültek. Ide menekült Niccolo fiúcska is az édesanyjával. Azt hitték, hogy a templomban menedéket lelnek, de a söpredék a templomba is betört, és kegyetlenül kaszabolta, öldöste az ott levő nőket és gyermekeket. Így kapott a kisfiú is több kardvágást, amelyek egyike az arcát érve felhasította a száját. A gyermek túlélte a vérengzést, de ettől fogva nehezen beszélt, hebegett. Kortársai ezért ragasztották rá a Tartaglia (dadogó) csúfnevet. Ez annyira megragadt rajta, hogy a matematikatörténet ma is gyakran így emlegeti. A nálunk Pascal-háromszög néven ismert elrendezést például az olasz iskolákban mind a mai napig Tartaglia háromszögének nevezik.
1. ábra: Niccolo Fontana (Tartaglia)
Nem kapott rendszeres iskolai képzést, édesanyjának csak arra telt, hogy fiát 14 éves korában 15 napig járassa iskolába. De Fontana 23 éves korában már matematikával kereste a kenyerét. Önállóan tanulta a matematikát és a latint, amely a tudomány nemzetközi nyelve volt. Számolómesterként pedig a hozzá forduló iparosok, építészek és kereskedők gyakorlati számítási problémáit oldotta meg, és így legalább akkora hírnév és megbecsülés övezte, mintha egyetemi katedrája lett volna.
A matematikatörténetbe Fontana a harmadfokú egyenlet általános megoldási módszerének ‐ egyik ‐ fölfedezőjeként írta be a nevét.
Úgy tűnik, hogy először Scipione del Ferro (1465‐1526) bolognai matematikus találta meg a harmadfokú egyenletek egy csoportjának az általános megoldási eljárását 1515 körül ([6] 172. old.). Ő az (, ) alakú egyenletek megoldási eljárását fedezte fel. (Az ilyen, (, ) harmadfokú egyenletet nevezték del Ferro típusú egyenletnek.) Titkát sokáig megtartotta, csak halála előtt nem sokkal árulta el vejének, Annibale della Nave professzornak, aki az utóda lett a bolognai egyetemen, ezenkívül a bresciai Antonio Maria Fiore professzortársával közölte a megoldóképletet.
Akkoriban divatos volt a ,,matematikai párbaj''. A másik problémáit igyekezett a két résztvevő megoldani a tudomány, saját maguk és párfogóik nagyobb dicsőségére. A győztes hírneve nőtt, de a vesztes sem bűnhődött túl szigorúan; följegyezték a krónikák, hogy egy esetben például vendégül kellett látnia a győztest és annak 29 barátját. Érthető, hogy a harmadfokú egyenlet megoldásának ismerete az ilyen párbajok során szinte legyőzhetetlenné tette a titok tudóját.
Általunk most nem tárgyalt előzmények után 1535-ben del Ferro módszerének ismeretében Antonio Maria Fiore egyetemi professzor matematikai párbajra hívta ki Tartaglia számolómestert. Tartaglia tudta, hogy Fiore ismeri az típusú harmadfokú egyenlet megoldóképletét, így arra számított, hogy ellenfele neki is ilyen típusú problémákat tűz majd ki. Ezért gőzerővel látott neki a kutatásnak, és az 1535. február 13-ra virradó éjszaka meg is találta az említett típusú harmadfokú egyenletek megoldásának titkát, néhány nap múlva pedig az (, ) típusúakét is.
A Nagy Matematikaverseny 1535. február 22-én zajlott le. Tartaglia két óra alatt megoldotta Fiore valamennyi problémáját, aki viszont egyetlen eggyel sem boldogult ellenfele problémái közül. Így az iskolázatlan számolómester legyőzte kihívóját, az egyetemi professzort, aki ráadásul nem is maga fedezte fel azt a képletet, amit tudott, hanem Scipione del Ferro professzortól tanulta.
Valószínűleg az történhetett, hogy Fiore típusú egyenleteket tűzött ki, míg Tartaglia (, ) típusú egyenleteket adott fel a professzornak. Ő mindkét változattal elboldogult, míg Fiore csak a saját maga által kitűzött típussal. Ezt erősíti meg a skóciai Szent András Egyetem matematikatörténeti adatbázisa is a Tartaglia címszónál [7]. Érdekes lenne megtudni a Nagy Matematikaverseny problémáit, de arról nem hallottam, hogy ezek fönnmaradtak volna.
A történet folytatását Sain Márton: Nincs királyi út c. könyvében [1] olvashatjuk. Megemlítjük azért, hogy a harmadfokú egyenlet általános megoldóképletét sem Ferroról, sem Tartagliaról, hanem Girolamo Cardano-ról (ld. 2. ábra) (1501‐1576) nevezték el. Ő a Tartagliatól megtudott megoldóképletet nem tartotta tovább titokban, hanem Ars magna sive de regulis algebraicis (A nagy tudomány, azaz az algebra törvényeiről) című, 1545-ben Nürnbergben megjelent művében közzétette az eredményt. Becsületesen leírja könyvében, hogy a harmadfokú egyenlet megoldóképletét ő Tartagliatól hallotta.
A harmadfokú egyenlet olyan alakja, amely az , és (, ) egyenleteket egyaránt magában foglalja: (, tetszőleges valós számok.) A Cardano-formula ismert alakja: | |
A del Ferro által megoldott eset pozitív -nek és negatív -nak felel meg.
Jól látható, hogy a jelentéktelennek tűnő különbség, a negatív esete miért okozhatott megoldhatatlannak látszó nehézséget: az egyenletre (gyökei nyilvánvaló szorzattá alakítás után , , ) alkalmazva például a titokzatos alak adódik, és a kortársak nem nagyon tudtak mit kezdeni a negatív számok rejtélyes négyzetgyökével.
Ha nem is tudjuk felidézni a Nagy Matematikaverseny példáit, azért megvizsgáljuk Tartaglia számolómester egy fennmaradt versenypéldáját. Azért nevezem versenypéldának, mert könnyen elképzelhető, hogy Tartaglia a versenyen is tűzött ki hasonló jellegű problémát.
Osszuk fel a -at két részre úgy, hogy e két résznek és a részek különbségének a szorzata maximális legyen.
Tartaglia a megoldás módszerét szokásához híven titokban tartotta, és csak a végeredményt közölte: A két rész különbségének négyzete legyen egyenlő a fél része négyzetének és ennek a harmadának összegével.
Ez kissé lakonikus feleletnek tűnik, ezért a problémát és Tartaglia válaszát is lefordítjuk az algebra nyelvére.
A Tartaglia-probléma algebrai jelölésekkel: Keressük az és pozitív számokat, amelyekre , és az szorzat maximális. Maximum esetén nyilván .
Tartaglia válasza algebrai jelölésekkel: az és olyan számok, amelyekre mellett az is teljesül, hogy Tehát és így Innen és . Tartaglia azt állította, hogy esetén az és számokra lesz maximális az szorzat. Mindenesetre meglepődhettek azok, akikkel csupán így közölte Tartaglia a választ. Hogyan tudták ellenőrizni, hogy jó-e az eredmény? Ezt nem tudom, de arra lehet gondolni, hogy miután nem tudtak olyan , számpárt mondani, amelyre nagyobb lett volna az szorzat, mint a Tartaglia számpárjánál adódó , elfogadták a választ. Tartaglia végeredménye valóban helyes, és ezt fogjuk a továbbiakban bebizonyítani.
Próbáljuk meg rekonstruálni Tartaglia eljárását. Vezessük be ismeretlenként a két rész különbségét: (). Ekkor, figyelembe véve, hogy , Így a következő függvény maximumát kell meghatároznunk: | |
ha .
Ma már a legtöbb érettségiző meg tudja oldani a feladatot (ha tanult deriválni), de a differenciálszámítást több, mint 150 évvel később fedezte föl Newton és Leibniz. Nézzük, hogyan gondolkodhatott Tartaglia a harmadfokú egyenletek tudósaként.
Jelöljük -mel az függvény maximumát a bővebb halmazon. Ekkor arra az -re, amelyre a függvény felveszi a maximumát fennáll, hogy Ezt rendezve az harmadfokú egyenletet kapjuk, és ennek az egyenletnek gyöke a maximumot szolgáltató .
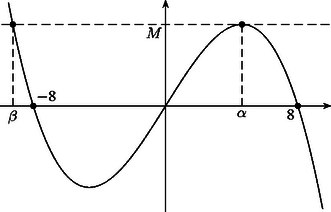
Azt a legnagyobb értéket keressük, amelyre a egyenletnek van pozitív gyöke. Bár Tartaglia idejében ‐ és még többszáz évig ‐ nem beszéltek függvényekről, és nem rajzoltak grafikonokat, mi fölrajzoljuk az függvény grafikonját,(3.ábra) hogy lássuk azt, amit ő nyilván egészen más módon látott át.
A keresett értékre mindenesetre az egyenletnek két gyöke van, egy pozitív, és egy negatív, . Az típusú egyenletek szakértőjeként pedig Tartaglia tudhatta, hogy ha az egyenletnek két gyöke van ‐ ma úgy mondanánk, hogy kétszeres gyök ‐, akkor a Cardano-formulában a négyzetgyök alatt álló mennyiség értéke 0.
Most , , és így a összefüggésből miatt , ez tehát a maximum értéke, az egyenlet pedig
A Cardano-formula az egyenlet ‐ egyik ‐ gyökét is kiszámolja: most . Láthatjuk ‐ például a grafikonról ‐, hogy ez az egyszeres gyök. Egy harmadfokú egyenlet egy gyökét ismerve viszont kiemelhetjük a megfelelő elsőfokú gyöktényezőt: | |
vagy a csak 1540-ben megszülető Vite-ről elnevezett formulákra hivatkozva megállapíthajtuk, hogy az típusú egyenlet gyökeinek az összege 0, és így , .
Hogy Tartaglia így okoskodott-e vagy másképp, nem tudhatjuk. Egy bizonyos értelemben sokkal többet kellett tudnia, hiszen a Nagy Matematikaverseny problémáit megoldva abban az esetben is elődta állítani a harmadfokú egyenlet gyökeit, amikor, mint az idézett példában, negatív szám volt a négyzetgyök alatt. Így, úgy, vagy másképpen, de a keresett értékhez már hozzá tudott férni. Innen pedig , , és valóban: .
Az eredmény Tartagliatól származó formája azt látszik sugallni, hogy ő talán értékét határozta meg az ; feltételből. Erre azonban nem látszik közvetlen út.
Befejezésül nézzük meg, hogy egy mai diák hogyan oldhatná meg elemi úton Tartaglia feladatát.
Az -ben három kifejezés szorzatát láthatjuk, és erről esetleg eszünkbe juthat a számtani és mértani közép közötti egyenlőtlenség három számra fennálló alakja. Mint tudjuk, minden nemnegatív , és valós számra, és itt pontosan akkor van egyenlőség, ha .
Ezzel közvetlenül nem sokra mennénk, mert ekkor | |
Az egyenlőtlenség természetesen igaz, de bal oldalon is változót tartalmazó kifejezés áll, így nem mutatja a jobb oldal maximumát. Arra kellene törekedni, hogy a bal oldalon konstans álljon.
Az függvénynek pontosan ugyanazon helyen van maximuma, mint az függvénynek, hiszen esetén az függvény nemnegatív. Emeljük tehát négyzetre -et. | |
Innen láthatjuk, hogy ha 2-vel megszorozzuk az egyenletet, akkor a jobb oldali három tényező összegében már kiesik az változó. | |
Ha most alkalmazzuk a számtani és mértani közép közötti egyenlőtlenséget a , , számokra, akkor azt kapjuk, hogy | |
Innen az maximuma esetén: Meg kell határoznunk még, hogy milyen -re veszi fel az függvény a maximumát.
Az -re kapott egyenlőtlenségben pontosan akkor áll egyenlőség, amikor a számtani közép egyenlő a mértani középpel. Ez, mint tudjuk, akkor és csak akkor teljesül, ha a három szám egyenlő egymással. Vagyis: Ebből , tehát (hiszen ). Így az kétismeretlenes egyenletrendszert megoldva kapjuk, hogy Tehát ezekre a számokra lesz maximális a vizsgált szorzat, amint azt már az előbb is láttuk.
Feladatok
1. Oldjuk meg a Tartaglia-problémát kissé általánosabban: tekintsük a pozitív számot, és ezt bontsuk fel két olyan és pozitív szám összegére, amelyekre maximális lesz az szorzat!
2. Írjunk adott sugarú gömbbe maximális térfogatú hengert!
Johannes Kepler (1571‐1630) nagy német csillagász alighanem az 1615-ben megjelent Stereometria doliorum vinorum (A boroshordók térmértana) című művében foglalkozott ezzel a problémával. A probléma szoros kapcsolatban van a Tartaglia feladattal, és lényegében hasonló módon oldható meg.
| * | [1]Sain Márton: Nincs királyi út! Matematikatörténet, Gondolat, Budapest, 1986. |
| * | [2]Sain Márton: Matematikatörténeti ABC (5., átdolgozott és bővített kiadás), Tankönyvkiadó, Budapest, 1987. |
| * | [3]Struik, Dirk, J.: A matematika rövid története, Gondolat, Budapest, 1958. |
| * | [4]Tikhomirov, Vladimir, M.: Stories about Maxima and Minima, American Mathematical Society, 1990. Mathematical Association of America, 1990. |
| * | [5]Freud Róbert (szerk): Nagy pillanatok a matematika történetében, Gondolat, Budapest, 1981. 2. fejezet. |
| * | [6]Eves, Howard: Great Moments in Mathematics (Before 1650), Mathematical Association of America, 1980, Lecture 16. |
| * | [7]h t t p : / / w w w - h is t o r y . m c s . s t - a n d r e w s . a c . u k / his t o r y / M a t h e m a t i c i a n s |
Érdekes regény: John Banville: Kepler, Európa Könyvkiadó, Budapest, 1963.
Csete Lajos, Markotabödöge
A kor matematikájában ‐ és még vagy 200 évig ‐ az ilyen típusú, főleg gyakorlati eredetű szélsőérték problémáknál egyáltalán nem vetődött föl, hogy létezik-e a szóban forgó
maximum. |
 PDF | MathML
PDF | MathML